Combined separable signals based neuro-fuzzy Hammerstein–Wiener model

Abstract

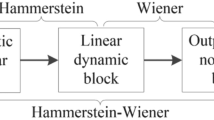
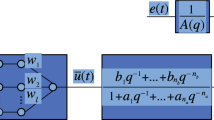
Hammerstein–Wiener model can describe a large number of complicated industrial processes. In this paper, a novel identification method for neuro-fuzzy based Hammerstein–Wiener model is presented. A neuro-fuzzy system with correlation analysis based non-iterative parameter updating algorithm is proposed to model the static nonlinearity of Hammerstein–Winer processes. As a result, the proposed method not only avoid the inevitable restrictions on static nonlinear function encountered by using the polynomial approach, but also overcomes the problems of initialization and convergence of the model parameters, which are usually resorted to trial and error procedure in the existing iterative algorithms used for the identification of Hammerstein–Winer model. In addition, combined separable signals are adopted to identify the Hammerstein–Wiener process, resulting in the identification problem of the linear model separated from that of nonlinear parts. Moreover, one part of the input signals is extended to more general signals, such as binary signals, Gaussian signals or other modulated signals. Examples are used to illustrate the effectiveness of the proposed method.

Appendix

The cross-correlation of u(k) and v(k) is

$$\begin{aligned} R_{vu} (\tau )=E\left( {v(k)u(k-\tau )} \right) ,\forall \tau \in Z \end{aligned}$$

(50)

According to the property of total expectation of random variable, above cross-correlation can be expressed as

$$\begin{aligned} R_{vu} (\tau )=E\left( {E\left( {v(k)u(k-\tau )|u(k)} \right) } \right) \end{aligned}$$

(51)

Furthermore, from $v(k)=f(u(k))$, we have

$$\begin{aligned} R_{vu} (\tau )=E\left( {v(k)E\left( {u(k-\tau )|u(k)} \right) } \right) \end{aligned}$$

(52)

As mentioned in [14, 18], we know that the separability of a process means that the conditional expectation $E\left( {u(k-\tau )|u(k)} \right)$ should satisfy

$$\begin{aligned} E\left( {u(k-\tau )|u(k)} \right) =a(\tau )u(k) \end{aligned}$$

(53)

where, $a(\tau )=R_u (\tau )/R_u (0)$

From Eqs. (52) and (53), we get

$$\begin{aligned} R_{vu} (\tau )=a(\tau )E\left( {v(k)u(k)} \right) \end{aligned}$$

(54)

In addition, the auto-correlation of u(k) is

$$\begin{aligned} R_u (\tau )=E\left( {u(k)u(k-\tau )} \right) ,\forall \tau \in Z \end{aligned}$$

(55)

According to the properties of expectation and total expectation of random variables, we obtain

$$\begin{aligned} R_u (\tau )= & {} E\left( {E\left( {u(k)u(k-\tau )|u(k)} \right) } \right) \nonumber \\= & {} E\left( {u(k)E\left( {u(k-\tau )|u(k)} \right) } \right) \end{aligned}$$

(56)

From Eq. (53), we have

$$\begin{aligned} R_u (\tau )=a(\tau )E\left( {u(k)u(k)} \right) \end{aligned}$$

(57)

From Eqs. (54) and (57), we get

$$\begin{aligned} R_{vu} (\tau )=\frac{E\left( {v(k)u(k)} \right) }{E\left( {u(k)u(k)} \right) }R_u (\tau ) \end{aligned}$$

(58)

Define $b_0 =\frac{E\left( {v(k)u(k)} \right) }{E\left( {u(k)u(k)} \right) }$, we thus have $R_{vu} (\tau )=b_0 R_u (\tau )$.

This completes the proof.