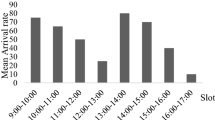
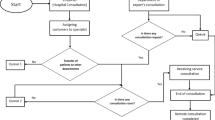
Abstract
Each patient is assigned to a specific scanner in CT department of a large-size hospital. Emergency patients have non-preemptive priority access to service. The service time of each CT scanner follows an Erlang distribution by data analysis from this hospital. We develop an M/E k /1 queueing model with emergency non-preemptive priority. Firstly, the expected waiting time of the jth phase regular patient in the waiting queue is given by Laplace transform. Using this and generating function of the steady-state of phase distribution, the expected waiting time of an arbitrary regular patient is obtained. A total cost function which includes the penalty cost for unutilized medical resources and waiting cost of regular patients is constructed. The optimal arrival rate of regular patients so as to minimize the total cost is given by Kuhn–Tucker condition. Some numerical examples which are based on real data are given.




Similar content being viewed by others
References
Afeche P, Mendelson H (2004) Pricing and priority auctions in queueing systems with a generalized delay cost structure. Manag Sci 50:869–882
Allon G, Hanany E (2012) Cutting in line: social norms in queues. Manag Sci 58:493–506
Anderson C, Butcher C, Moreno A (2010) Emergency department patient flow simulation at HealthAlliance. Project proposal, Worcester Polytechnic Institute, Worcester: MA, (Chapter 1)
Boxma OJ, van der Wal J, Yechiali U (2008) Polling with batch service. Stoch Models 24(4):604–625
Eric PJ, Thomas LP (2009) A review and synthesis of demand management, capacity management and performance in health-care services. Int J Manag Rev 11:149–174
Gómez-Corral A, Krishnamoorthy A, Narayanan VC (2005) The impact of self-generation of priorities on multi-server queues with finite capacity. Stoch Models 21:427–447
Green L, Savin S, Wang B (2006) Managing patient demand in a diagnostic medical facility. Oper Res 54:11–25
Gupta D, Wang L (2008) Revenue management for a primary-care clinic in the presence of patient choice. Oper Res 56:576–592
He QM, Chavoushi AA (2013) Analysis of queueing systems with customer interjections. Queueing Syst 73:79–104
Krishnamoorthy A, Babu S, Narayanan VC (2008) MAP/(PH/PH)/c queue with self-generation of priorities and non-preemptive service. Stoch Ana Appl 26:1250–1266
Krishnamoorthy A, Babu S, Narayanan VC (2009) The MAP/(PH/PH)/1 queue with self-generation of priorities and non-preemptive service. Eur J Oper Res 195:174–185
Krishnamoorthy A, Narayanan VC, Deepak TG (2005) On a queueing system with self generation of priorities. Neural Parallel Sci Comput 13:119–130
Luo J, Kulkarni V, Ziya S (2012) Appointment scheduling under patient no-shows and service interruptions. Manuf Serv Oper Manag 14:670–684
Meng YK (1989) The foundation of queueing theory and application. Tongji University Press, Shanghai (Chapter 5, in Chinese)
Perel N, Yechiali U (2013) The Israeli queue with priorities. Stochas Models 29:353–379
Ross M (2007) Introduction to probability models, 9th edn. Academic Press, Inc., Orlando (Chapter 2)
Wang HK, Huang HM (1995) Optimal control of a removable server in an M/E k /1 queueing system with finite capacity. Microelectron Reliab 35:1023–1030
Wang Q (2004) Modeling and analysis of high risk patient queues. Eur J Oper Res 155:502–515
Zhang HB, Shi DH (2010) Explicit solution for M/M/1 preemptive priority queue. Int J Inf Manag Sci 21:197–208
Acknowledgments
This research is partially supported by National Natural Science Foundation of P.R. China (71490722, 71490725, 71301111), Research Project of Education Department of Sichuan Province (13ZB0140), National Social Science Foundation of P.R. China (15BGL198). We would like to express our great thankfulness to the anonymous reviewers for their constructive suggestions and encouragement. We thank the administrators, medical staff at Sichuan Provincial People’s Hospital for their contribution to this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhou, J., Li, J. An M/E k /1 queues with emergency non-preemptive priority of a diagnostic resource. Oper Res Int J 17, 1–16 (2017). https://doi.org/10.1007/s12351-015-0211-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12351-015-0211-z