Abstract
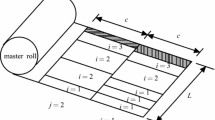
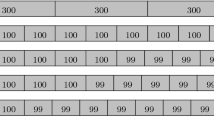
This paper considers the cutting stock problem with frustum of cone bars. A multiple objective optimization model is established by taking into account trim loss, the number of cutting patterns and usable leftovers. A decision-making method for solving this cutting stock problem is designed. First, an improved non-dominated sorting heuristic evolutionary algorithm is developed for generating the Pareto non-dominated solutions. Then the weights of the objectives are calculated by combining the subjective methods (subjectively determined by the decision maker) and objective methods (objectively determined by numerical computing). Finally, a multi-attribute decision making method is used for choosing a cutting plan from the Pareto non-dominated solutions. Computational results indicate that the method proposed is feasible.





Similar content being viewed by others
References
Adriana CC, Marcos NA, Horacio HY (2009) The one-dimensional cutting stock problem with usable leftover—a heuristic approach. Eur J Oper Res 3:897–908
Cheng Q (2010) Strueture entropy weight method to confirm the weight of evaluating index. Syst Eng Theory Pract 7:1225–1228
Claudio A, Fabrizio M (2014) On cutting stock with due dates. Omega 46:11–20
Cui YD, Yang YL (2010) A heuristic for the one-dimensional cutting stock problem with usable leftover. Eur J Oper Res 2:245–250
Cui YD, Zhong C, Yao Y (2015) Pattern-set generation algorithm for the one-dimensional cutting stock problem with setup cost. Eur J Oper Res 243:540–546
Deb K, Pratap A, Agrawal S (2002) A fast and elitist multi objective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 2:182–197
Erjavec J, Gradisar M, Trkman P (2012) Assessment of stock size to minimize cutting stock production costs. Int J Prod Econ 135:170–176
Goldberg DE (1989) Genetic algorithms in search, optimization, and machine learning. Addison-Wesley, MA
Gracia C, Andrés C, Gracia L (2013) A hybrid approach based on genetic algorithms to solve the problem of cutting structural beams in a metalwork company. J Heuristics 19:253–273
Harald R, Thomas WMV (2010) The one-dimensional cutting stock problem with due dates. Eur J Oper Res 3:701–711
Hwang CL, Yoon K (1981) Multiple attribute decision making: methods and applications. Springer, New York
Lin XY, Wang Y (2003) On optimization for multi-objective cutting problem. Nat Sci J Harbin Norm Univ 5:14–16
Liu R, Yan X, Chen F (2010) One-dimension layout system considering multi-objective optimization. Comput Appl Softw 1:23–25
Vacharapoom B, Sdhabhon B (2014) Three-step solutions for cutting stock problem of construction steel bars. J Civil Eng 5:1239–1247
Wang ZY, Gu HF, Yi XY (2003) A method of determining the linear combination weights based on entropy. Syst Eng Theory Pract 3:112–116
Yan CP, Song TF, Liu F (2010) Manufacturability-oriented one-dimensional cutting-stock problem under complex constraints status. Comput Integr Manuf Syst 1:195–201
Zheng XJ, Hang YG, Teng HF (2009) Simulated annealing algorithm based on satisfaction degree for one-dimensional cutting-stock problems with multiple stock lengths. J Dalian Univ Technol 6:865–871
Acknowledgments
Supported by the Decision Science and Technology Research Institute, Hefei University of Technology, Hefei, China is gratefully appreciated. This research was supported in part by the National Natural Science Foundation under the Grant Nos.: 71171071, 71231004 and Anhui Universities Natural Science Project under the Grant No.: KJ2011A215.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Liu, L., Liu, X., Pei, J. et al. A study on decision making of cutting stock with frustum of cone bars. Oper Res Int J 17, 187–204 (2017). https://doi.org/10.1007/s12351-015-0221-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12351-015-0221-x