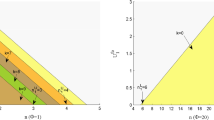
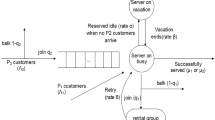
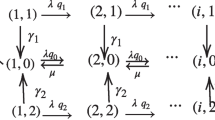Abstract
The strategic joining behavior of customers in a single-server Markovian queueing system with Bernoulli vacation is studied. It is assumed that the server begins a vacation period if the queue is empty upon completion of a service, and if the queue is not empty, the server will take a Bernoulli type vacation. Assuming that arriving customers can observe various levels of the system information, we study strategic customers’ decision on whether to join or balk the queue based on a linear reward-cost structure. The Nash equilibrium strategies in the fully observable case and the unobservable cases are investigated. The effect of the information level as well as several parameters on the equilibrium behavior is illustrated via numerical examples.









Similar content being viewed by others
References
Burnetas A, Economou A (2007) Equilibrium customer strategies in a single server Markovian queue with setup times. Queueing Syst 56:213–228
Chen P, Zhou Y (2015) Equilibrium balking strategies in the single server queue with setup times and breakdowns. Oper Res Int J 15:213–231
Economou A, Gomez-Corral A, Kanta S (2011) Optimal balking strategies in single-server queues with general service and vacation times. Perform Eval 68:967–982
Economou A, Kanta S (2008) Equilibrium balking strategies in the observable single-server queue with breakdowns and repairs. Oper Res Lett 36:696–699
Ghafir HM, Silio CB (1993) Performance analysis of a multiple access ring network. IEEE Trans Commun 41:1494–1506
Guo P, Hassin R (2011) Strategic behavior and social optimization in Markovian vacation queues. Oper Res 59:986–997
Guo P, Hassin R (2012) Strategic behavior and social optimization in Markovian vacation queues: the case of heterogeneous customers. Eur J Oper Res 222:278–286
Guo P, Li Q (2013) Strategic behavior and social optimization in partially-observable Markovian vacation queue. Oper Res Lett 41:277–284
Hassin R, Haviv M (2003) To queue or not to queue: equilibrium behavior in queueing systems. Kluwer Academic Publishers, Boston
Keilson J, Servi LD (1986) Oscillating random walk models for GI/G/1 vacation system with Bernoulli schedules. J Appl Probab 23:790–802
Kumar BK, Madheswari SP (2009) Analysis of an M/M/N queue with Bernoulli service schedule. Int J Oper Res 5:48–72
Kumar BK, Rukmani R, Thangaraj V (2009) An M/M/C retrial queueing system with Bernoulli vacations. J Syst Sci Syst Eng 18:222–242
Kumar BK, Rukmani R, Lakshmi SA (2013a) Performance analysis of an M/G/1 queueing system under Bernoulli vacation schedules with server setup and close down periods. Comput Ind Eng 66:1–9
Kumar BK, Madheswari SP, Lakshmi SRA (2013b) AnM/G/1 Bernoulli feedback retrial queueing system with negative customers. Oper Res Int J 13:187–210
Liu W, Ma Y, Li J (2012) Equilibrium threshold strategies in observable queueing systems under single vacation policy. Appl Math Model 36:6186–6202
Ramaswamy R, Servi LD (1988) The busy period of the M/G/1 vacation model with a Bernoulli schedule. Commun Stat Stoch Models 4:507–521
Servi LD (1986) Average delay approximation of M/G/1 cyclic service queue with Bernoulli schedule. IEEE J Sel Areas Commun 4:813–820
Stidham S Jr (2009) Optimal design of queueing systems. CRC Press, Boca Raton
Sun W, Guo P, Tian N (2010) Equilibrium threshold strategies in observable queueing systems with setup/closedown times. Cent Eur J Oper Res 18:241–268
Takagi H (1991) Vacation and priority systems, queueing analysis: a foundation of performance evaluation, vol 1. North-Holland, New York
Tian N, Zhang ZG (2006) Vacation queueing models: theory and applications. Springer, New York
Wang J, Cao J, Li Q (2001) Reliability analysis of the retrial queue with server breakdowns and repairs. Queueing Syst 38:363–380
Wang J, Zhang F (2011) Equilibrium analysis of the observable queues with balking and delayed repairs. Appl Math Comput 218:2716–2729
Acknowledgments
The authors thank the editor and three anonymous referees for their valuable comments and suggestions of improving the quality of this paper. This work was supported by the National Natural Science Foundation of China (Grant Nos. 11171019, 71390334 and 71571014).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1. The functions S(0, q(0), q(1)) and S(1, q(0), q(1)) are both strictly decreasing for \(q(1)\in [0,1]\).
Proof
Denote the expected mean sojourn time of an arriving customer who decides to enter at state i by \(E[W_i]\). Then we have
It is readily to verify that \(E[W_0]\) and \(E[W_1]\) are increasing for \(\lambda _0 \in [0,1]\), respectively. Next we will prove that \(E[W_0]\) and \(E[W_1]\) are all increasing for \(\lambda _1 \in [0,1]\).
Firstly, we prove that \(E[W_0]\) is increasing for \(\lambda _1 \in [0,1]\).
Letting
where \(x \in [0,1]\).
From the above equation, we can observe that the first part is increasing for \(x \in [0,1]\), then we only need to give the evidence of the latter part.
We let
Obviously, Eq. (62) is strictly increasing for \(x \in [0,1]\). Now differentiating (63) with respect to x, we obtain
By using the condition \(\mu \theta >\lambda (\mu p+\theta )\), we get
That is, we get \(g_2^{'}(x)>0\) for \(x \in [0,1]\), which follows that Eq. (63) is strictly increasing for \(x \in [0,1]\). From the above discussion, we can get that g(x) is strictly increasing for \(x \in [0,1]\), i.e., \(E[W_0]\) is increasing for \(\lambda _1 \in [0,1]\).
Similarly, we can prove that \(E[W_1]\) is increasing for \(\lambda _1 \in [0,1]\). \(\square\)
2. In the fully unobservable M/M/1 queue with Bernoulli vacation, the system is stable if and only if \(\mu \theta >\lambda q(\mu p+ \theta ).\)
Proof
Firstly, we prove the necessity of the condition, i.e. if the system is stable, then \(\mu \theta >\lambda q(\mu p+ \theta ).\)
As we have already obtained the probability generating functions \(P_0(z)\) and \(P_1(z)\) in Proposition 4.1, plugging \(z=1\) in Eqs. (21) and (22), we can get
If the system is stable, then the following conditions are established:
where \(\lambda _0=\lambda _1=\lambda\).
Through combining the expression of p(0, 0) [i.e. Eq. (23)] which has been obtained in the proof of Proposition 4.1, we can get the condition \(\mu \theta >\lambda q(\mu p+ \theta )\).
In other words, the interpretation of this stability condition could be referred to Theorem 3.1. of Wang et al. (2001), i.e., “the generalized service time of a single customer (i.e., \(\frac{\theta +\mu p}{\mu \theta }\)) is less than the interarrival time between two customers (i.e., \(\frac{1}{\lambda q}\))”.
Next, we prove that the inequality \(\mu \theta >\lambda q(\mu p+ \theta )\) is also a sufficient condition for the system to be stable. We use the method in Theorem 3.1. of Wang et al. (2001). Because of the Markovian property of the system in our paper, here \(\Psi _k=E(Q_{n+1}-Q_n|Q_n=k)\) equals the mean number of customers arriving during the generalized service time minuses 1, i.e.,
Obviously, if \(\mu \theta >\lambda q(\mu p+ \theta )\), we can obtain that the system is stable. \(\square\)
Rights and permissions
About this article
Cite this article
Liu, J., Wang, J. Strategic joining rules in a single server Markovian queue with Bernoulli vacation. Oper Res Int J 17, 413–434 (2017). https://doi.org/10.1007/s12351-016-0231-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12351-016-0231-3