Skip to main content

Advertisement

Springer Nature Link
Log in

Portfolio selection in a regime switching market with a bankruptcy state and an uncertain exit-time: multi-period mean–variance formulation

  • Original Paper
  • Published:
Operational Research Aims and scope Submit manuscript

Abstract

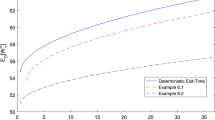
This paper studies three versions of the multi-period mean–variance portfolio selection problem, that are: minimum variance problem, maximum expected return problem and the trade-off problem, in a Markovian regime switching market where the exit-time is uncertain and exogenous. The underlying Markov chain contains an absorbing state, which denotes the bankruptcy state. When the Markov chain switches to this state, the investors only get a random fraction, known as the recovery rate, taking values in [0, 1] of their wealth. Asset returns, as well as recovery rate, depend on the market state. Dynamic programming and Lagrange duality method are used to derive analytical expressions for optimal investment strategies and the mean–variance efficient frontier. It is shown that portfolio selection models with no bankruptcy state and certain exit-time can be considered as special cases of our model. Some numerical examples are provided to demonstrate the effect of the recovery rate and exit-probabilities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. In fact \(\omega _{k+1}(j)>0\) for all \(j\in {\mathbb {S}}\), if we assume that \(r_{n,0}(L)>0\) for all n (see (7)).

  2. They considered a market with \(n\ge 1\) risky assets and solved problem \(P(\omega )\).

  3. They considered a market with \(n\ge 1\) risky assets and assumed that the asset returns depend only on the market state but not the time period and solved problems \(P(\mu )\), \(P(\sigma )\) and \(P(\omega )\).

References

  • Bauerle N, Rieder U (2004) Portfolio optimization with Markov-modulated stock prices and interest rates. IEEE Trans Autom Control 49(3):442–447

    Google Scholar 

  • Cakmak U, Ozekici S (2006) Portfolio optimization in stochastic markets. Math Methods Oper Res 63(1):151–168

    Google Scholar 

  • Canakoglu E, Ozekici S (2009) Portfolio selection in stochastic markets with exponential utility functions. Ann Oper Res 166(1):281–297

    Google Scholar 

  • Canakoglu E, Ozekici S (2010) Portfolio selection in stochastic markets with HARA utility functions. Eur J Oper Res 201(2):520–536

    Google Scholar 

  • Canakoglu E, Ozekici S (2011) Portfolio selection with imperfect information: a hidden Markov model. Appl Stoch Models Bus Ind 27(2):95–114

    Google Scholar 

  • Canakoglu E, Ozekici S (2012) HARA frontiers of optimal portfolios in stochastic markets. Eur J Oper Res 221(1):129–137

    Google Scholar 

  • Celikyurt U, Ozekici S (2007) Multiperiod portfolio optimization models in stochastic markets using the mean–variance approach. Eur J Oper Res 179:186–202

    Google Scholar 

  • Chen P, Yang HL, Yin G (2008) Markowitz’s mean–variance asset-liability management with regime switching: a continuous-time model. Insur Math Econ 43(3):456–465

    Google Scholar 

  • Chen Z, Li G, Zhao Y (2014) Time-consistent investment policies in Markovian markets: a case of mean–variance analysis. J Econ Dyn Control 40:293–316

    Google Scholar 

  • Chen ZP, Liu J, Li G (2016) Time consistent policy of multi-period mean–variance problem in stochastic markets. J Ind Manag Optim 12(1):229–249

    Google Scholar 

  • Cheung KC, Yang H (2004) Asset allocation with regime-switching: discrete-time case. Astin Bull 34(1):247–257

    Google Scholar 

  • Cheung KC, Yang H (2007) Optimal investment-consumption strategy in a discrete-time model with regime switching. Discrete Contin Dyn Syst Ser B 8(2):315–332

    Google Scholar 

  • Costa OLV, Araujo MV (2008) A generalized multi-period mean–variance portfolio optimization with Markov switching parameters. Automatica 44(10):2487–2497

    Google Scholar 

  • Elliott RJ, Siu TK, Badescu A (2010) On mean–variance portfolio selection under a hidden Markovian regime switching model. Econ Model 27(3):678–686

    Google Scholar 

  • Hakansson N (1969) Optimal investment and consumption strategies under risk, an uncertain lifetime, and insurance. Int Econ Rev 10(3):443–466

    Google Scholar 

  • Hakansson N (1971) Optimal entrepreuneurial decisions in a completely stochastic environment. Manag Sci 17(7):427–449

    Google Scholar 

  • Honda T (2003) Optimal portfolio choice for unobservable and regime-switching mean returns. J Econ Dyn Control 28(1):45–78

    Google Scholar 

  • Hu F, Wang R (2017) Optimal investment-consumption strategy with liability and regime switching model under value-at-risk constraint. Appl Math Comput 313:103–118

    Google Scholar 

  • Li D, Ng WL (2000) Optimal dynamic portfolio selection: multiperiod mean–variance formulation. Math Finance 10(3):387–406

    Google Scholar 

  • Li G, Chen ZP, Liu J (2016) Optimal policy for a time consistent mean–variance model with regime switching. IMA J Manag Math 27(2):211–234

    Google Scholar 

  • Luenberger DG (1968) Optimization by vector space methods. Wiley, New York

    Google Scholar 

  • Markowitz H (1952) Portfolio selection. J Finance 7(1):77–91

    Google Scholar 

  • Merton RC (1971) Optimal consumption and portfolio rules in a continuous-time model. J Econ Theory 3(4):373–413

    Google Scholar 

  • Sotomayor L, Cadenillas A (2009) Explicit solutions of consumption-investment problems in financial markets with regime switching. Math Finance 19(2):215–236

    Google Scholar 

  • Wei SZ, Ye ZX (2007) Multi-period optimization portfolio with bankruptcy control in stochastic market. Appl Math Comput 186(1):414–425

    Google Scholar 

  • Wu HL, Li ZF (2011) Multi-period mean–variance portfolio selection with Markov regime switching and uncertain time-horizon. J Syst Sci Complex 24(1):140–155

    Google Scholar 

  • Wu H, Li Z (2012) Multi-period mean–variance portfolio selection with regime switching and a stochastic cash flow. Insur Math Econ 50(3):371–384

    Google Scholar 

  • Wu H, Zeng Y (2013) Multi-period mean–variance portfolio selection in a regime-switching market with a bankruptcy state. Optim Control Appl Methods 34(4):415–432

    Google Scholar 

  • Wu HL, Zeng Y, Yao HX (2014) Multi-period Markowitz’s mean–variance portfolio selection with state-dependent exit probability. Econ Model 36:69–78

    Google Scholar 

  • Yaari M (1965) Uncertain lifetime, life insurance, and the theory of the consumer. Rev Econ Stud 32(2):137–150

    Google Scholar 

  • Yao H, Lai Y, Hao Z (2013) Uncertain exit time multi-period mean–variance portfolio selection with endogenous liabilities and Markov jumps. Automatica 49(11):3258–3269

    Google Scholar 

  • Yao H, Li X, Hao Z, Li Y (2016) Dynamic asset-liability management in a Markov market with stochastic cash flows. Quant Finance 16(10):1575–1597

    Google Scholar 

  • Yin G, Zhou XY (2004) Markowitz’s mean–variance portfolio selection with regime switching: from discrete-time to their continuous-time limits. IEEE Trans Autom Control 49(3):349–360

    Google Scholar 

  • Zeng Y, Wu H, Lai Y (2013) Optimal investment and consumption strategies with state-dependent utility functions and uncertain time-horizon. Econ Model 33:462–470

    Google Scholar 

  • Zhang L (2014) Continuous-time mean-variance asset-liability management with hidden Markovian regime switching. Math Probl Eng 2014:1

    Google Scholar 

  • Zhang M, Chen P (2016) Mean-variance portfolio selection with regime switching under shorting prohibition. Oper Res Lett 44(5):658–662

    Google Scholar 

  • Zhang L, Li Z, Xu Y, Li Y (2016) Multi-period mean variance portfolio selection under incomplete information. Appl Stoch Model Bus 32(6):753–774

    Google Scholar 

  • Zhang M, Chen P, Yao H (2017) Mean–variance portfolio selection with only risky assets under regime switching. Econ Model 62:35–42

    Google Scholar 

  • Zhou XY, Li D (2000) Continuous-time mean–variance portfolio selection: a stochastic LQ framework. Appl Math Opt 42(1):19–33

    Google Scholar 

  • Zhou XY, Yin G (2003) Markowitz’s mean–variance portfolio selection with regime switching: a continuous-time model. SIAM J Control Optim 42(4):1466–1482

    Google Scholar 

  • Zhu DM, Xie Y, Ching WK, Siu TK (2016) Optimal portfolios with maximum value-at-risk constraint under a hidden Markovian regime-switching model. Automatica 74:194–205

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Khansar Faculty of Mathematics and Computer Science, Khansar, Iran

    Reza Keykhaei

Authors
  1. Reza Keykhaei
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Reza Keykhaei.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Keykhaei, R. Portfolio selection in a regime switching market with a bankruptcy state and an uncertain exit-time: multi-period mean–variance formulation. Oper Res Int J 20, 1231–1254 (2020). https://doi.org/10.1007/s12351-018-0372-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12351-018-0372-7

Keywords