A genetic algorithm based approach to solve multi-resource multi-objective knapsack problem for vegetable wholesalers in fuzzy environment

Abstract

Vegetable wholesaling problem has a vital role in the business system. In this problem, a vegetable wholesaler is supposed to supply raw, fresh vegetables to supermarkets in an efficient way by minimizing time but maximizing profit. In this paper, we have presented a multi-resource multi-objective knapsack problem (MRKP) for vegetable wholesalers. This model is beneficial for a vegetable wholesaler who collects different types of vegetables (objects) from different villages (resources) to a market for selling the vegetables (objects). MRKP is an extension of the classical concept of 0–1 multi-dimensional knapsack problem (KP). In this model, precisely a wholesaler has a limited capacity van/trolley by which he/she collects a set of vegetables from different villages/vegetable fields. In this model, we have assumed that all the vegetables are available for each resource. Each type of vegetable is associated with a weight, a corresponding profit, and a collection time (for a particular resource). The profit, weight, and collection time of objects is different for different resources. Here a time slice is considered for each object to collect it from different villages to a particular destination/market. Also, the profit and time are the two objectives. MRKP aims to find the amount of an object and the corresponding resource name from which it is collected. We have solved the proposed problem in the fuzzy environment. In this paper, we have explained two defuzzification techniques, namely fuzzy expectation and total $\lambda$-integral value method to solve the proposed problem. We have explained a modified multi-objective genetic algorithm (NSGA-II by Deb et al. in IEEE Trans Evol Comput 6(2):192–197, 2002) that is to maximise the profit and minimise the time to collect the objects. We have considered a multi-objective benchmark test function to show the effectiveness of the proposed Genetic Algorithm. Modification is made by introducing refinement operation. An extensive computational experimentation has been executed that generates interesting results to establish the effectiveness of the proposed model.

Appendix A: Prerequisite mathematics

Fuzzy sets were introduced by Zadeh (1978) as a mathematical way of representing impreciseness or vagueness in everyday life.

1.1 Fuzzy set

A fuzzy set $\tilde{A}$ of the universe of discourse X is defined as the following set of pairs $\tilde{A}=\{(x,\mu _{\tilde{A} }(x)):x\in X\}.$ Here $\mu _{\tilde{A}}:X\rightarrow [0,1]$ is a mapping called the membership function of the fuzzy set $\tilde{A}$ and $\mu _{\tilde{A}}(x)$ is called the membership value or degree of membership of $x\in X$ in the fuzzy set $\tilde{A}$.

1.2 Triangular fuzzy number (TFN)

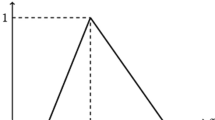
A TFN $\tilde{a}=(a_{1},a_{2},a_{3})$ has three parameters $a_{1},a_{2},$and$\ a_{3}$ where $a_{1}<a_{2}<a_{3}$ and is characterized by the membership function $\mu _{\tilde{a}}$, given by:

$$\begin{aligned} \mu _{\tilde{a}}(x)=\left\{ \begin{array}{l} \frac{x-a_{1}}{a_{2}-a_{1}}\quad \ \text {for}\ a_{1}\le x\le a_{2} \\ \frac{a_{3}-x}{a_{3}-a_{2}}\quad \ \text {for}\ a_{2}\le x\le a_{3} \\ 0,\quad \ \text {otherwise.} \end{array} \right. \end{aligned}$$

(A1)

1.3 Fuzzy expectation method

1.3.1 Fuzzy expectation (Liu 2009)

Let $\tilde{X}$ be any fuzzy variable in the possibility space $(\Theta ,P(\Theta ),Pos)$. The expected value of the fuzzy variable $\tilde{X}$ is denoted by $E(\tilde{X})$ and defined by

$$\begin{aligned} E(\tilde{X})=\int _{0}^{\infty }Cr(\tilde{X}\ge r)\,dr-\int _{-\infty }^{0}Cr( \tilde{X}\le r)\,dr. \end{aligned}$$

(A2)

When the right hand side of (A2) is from $\infty$ to $-\infty ,$ the expected value is not defined.

Lemma 1

[Liu (2009)] If $\tilde{j}=(j_{1},j_{2},j_{3})$ be a triangular fuzzy number, then the expected value of $\tilde{j}$ is $E[\tilde{j}]=\frac{1}{2}[(1-\rho )j_{1}+j_{2}+\rho j_{3}]$, where $0\le \rho \le 1$. Here, it is assumed that $\rho =0.5$.

1.4 Fuzzy total $\lambda$-integral value method

The total $\lambda$-integral value is a convex combination of the right and left integral values through the degree of optimism (Dey and Roy 2014). The left integral value is used to find the pessimistic viewpoint and the right integral value is used to find the optimistic viewpoint of the decision-maker. The value of $\lambda$ lies in the range [0, 1] for total $\lambda$-integral value method. The value of $\lambda$specifies the degree of optimism and pessimism.

1.4.1 Total $\lambda$-integral value (Dey and Roy 2014)

Let $\lambda$ is called degree of optimism, be a preassigned parameter and $\lambda \in [0,1]$. The graded mean value (or the total $\lambda$-integral value) of $\tilde{A}$ is defined as $I_{\lambda }(\tilde{A})=\lambda I_{R}(\tilde{A})+(1-\lambda )I_{L}(\tilde{A}),$ where $I_{R}(\tilde{A})$ and $I_{L}(\tilde{A})$ are the right and left interval values of $\tilde{A}$ and these are it is defined as:

$I_{R}(\tilde{A}) = \int _{0}^{1}(\mu _{R\tilde{A}})^{-1}\alpha \,d\alpha$, and $I_{L}(\tilde{A})= \int _{0}^{1}(\mu _{L\tilde{A}})^{-1}\alpha \,d\alpha$. Now, for $\tilde{h}=(h-\delta ,h,h+\delta )$

$$\begin{aligned} \mu _{\tilde{h}}(x) = \left\{ \begin{array}{ll} \mu _{L\tilde{h}}(x) = \frac{x - h + \delta }{\delta }&{}\quad \text { if } h - \delta \le x \le h \\ \mu _{R\tilde{h}}(x) = \frac{h + \delta - x}{\delta }&{}\quad \text { if } h \le x \le h + \delta \\ 0 &{}\quad \text { otherwise} \\ \end{array} \right. \end{aligned}$$

Now, using total $\lambda$-integral value we have to calculate:

$$\begin{aligned} I_{\lambda }(\tilde{h})=\lambda I_{R}(\tilde{h})+(1-\lambda )I_{L}(\tilde{h}) \end{aligned}$$

(A3)

where $I_{R}(\tilde{h})= \int _{0}^{1}(\mu _{R\tilde{h} })^{-1}\alpha d\alpha$ and $I_{L}(\tilde{h})= \int _{0}^{1}(\mu _{L\tilde{h} })^{-1}\alpha d\alpha$. Now, $(\mu _{R\tilde{h}})^{-1}\alpha = h + \delta -\alpha \delta$ and $(\mu _{L\tilde{h}})^{-1}\alpha = \delta \alpha + h - \delta$. Therefore, $I_{R}(\tilde{h})= h + \frac{\delta }{2}$, $I_{L}(\tilde{h}) = h - \frac{\delta }{2}$, and the total $\lambda$-integral value of $\tilde{h}$ is

$$\begin{aligned} I_{\lambda }(\tilde{h}) = \lambda \left( h+\frac{\delta }{2}\right) + (1 - \lambda )\left( h - \frac{\delta }{2}\right) = h + \lambda \delta - \frac{\delta }{2} = h + \left( \lambda - \frac{1}{2}\right) \delta \end{aligned}$$

(A4)