Equilibrium joining strategies in the M_n/G/1 queue with server breakdowns and repairs

Abstract

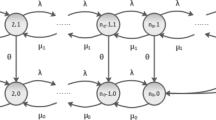
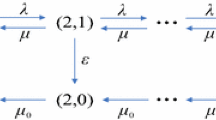
This paper considers an almost observable unreliable $M_{n}{/}G{/}1$ queueing system in which the arriving customers can observe the queue length upon their arrivals but not the state of the server. The arrival rates are state-dependent and the server is subject to breakdowns when it works. The lifetime of the server and the repair time are independent, and they follow two different general distributions. To obtain the steady-state queue length distribution, we present an auxiliary system called modified $M_{n}{/}G{/}1$ queueing system. Comparing the unreliable system with the modified system, we derive the steady-state queue length distributions at the arrival instant of a tagged customer. Moreover, we study customers’ equilibrium joining strategies based on a nonlinear waiting cost function. These results provide managerial insights into strategic behaviors of customers.

Appendix

Proof of Lemma 3.1

By the definition of distribution function, we have

$$ \begin{aligned} \hat{B}(x)&\;=\Pr (\hat{X_{i}} \le x)=Pr(\bar{X_{i}} \le x)=\Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x) \\&\;=\int _{0}^{x}\Pr (\sum _{j=1}^{N(t)}Y_{ij} \le x-t)dB(t)= \int _{0}^{x} \left[ \int _{0}^{\infty }\Pr (\sum _{j=1}^{z}Y_{ij} \le x-t)d_z\Psi _t(z) \right] dB(t), \end{aligned}$$

where $\Psi _t(z)=Pr(N(t)\le z)=\sum _{i=0}^{z}P_{t}(i)$. Since $Y_{ij}\sim G(x),i,j \in Z^{+}$, in virtue of the convolution formula, we get

$$ \hat{B}(x)=\int _{0}^{x} \left[ \int _{0}^{\infty }\tilde{G}^{(z)}(x-t)d_z\Psi _t(z) \right] dB(t). $$

(7.1)

This completes the proof. $\square$

Proof of Lemma 3.2

(1) The mean service time in modified $M_n{/}G{/}1$ system can be computed by

$$ \begin{aligned} E(\hat{X_{i}})&\;= E(\bar{X_{i}})=E(X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij}) =\beta _{1}+E[E(\sum _{j=1}^{N(X_{i})}Y_{ij}|N(X_{i}))] \nonumber \\&\;=\beta _{1}+\sum _{k=1}^{\infty }E\left[ \sum _{j=1}^{k}Y_{ij}|N(X_{i})=k\right] \Pr (N(X_{i})=k). \end{aligned}$$

(7.2)

The number of breakdowns $N(X_{i})$ is independent of $Y_{ij}, j=1,2,\ldots , N(X_{i})$, then (7.2) can be rewritten as

$$ E(\hat{X})=\beta _{1}+\sum _{k=1}^{\infty }E\left( \sum _{j=1}^{k}Y_{ij}\right) \Pr (N(X_{i})=k). $$

Since $Y_{ij}, j=1,2,\ldots , k$ are i.i.d random variables with the common mean value $\gamma _{1}$, we have that

$$ E(\hat{X_{i}})=\beta _{1}+\gamma _{1}\sum _{k=1}^{\infty }k\Pr (N(X_{i})=k)=\beta _{1}+\gamma _{1}\sum _{k=1}^{\infty }k\int _{0}^{\infty }P_{x}(k)dB(x), $$

where the last equation is by the total probability formula.

(2) According to the definition of the modified system, we know that the conditional mean remaining service time at the arrival instant of a tagged customer who finds n customers in the modified system is identical to the generalized conditional mean remaining service time in the unreliable system. This completes the proof. $\square$

Proof of Lemma 4.3

(1) By the definition of distribution, we have

$$ \begin{aligned} \hat{B}(x)&\;=\Pr (\hat{X_{i}} \le x)=\Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x) \nonumber \\&\;= \Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x,N(X_{i})=0) + \Pr (X_{i}+\sum _{j=1}^{N({X_{i})}}Y_{ij} \le x, N(X_{i})\ne 0). \end{aligned}$$

(7.3)

Next we prove that $\lim \limits _{\alpha \rightarrow 0}\Pr (X_{i}+\sum _{j=1}^{N({X_{i})}}Y_{ij} \le x, N(X_{i})\ne 0)=0$.

$$ \Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, N(X_{i})\ne 0)\le \Pr ( N(X_{i})\ne 0), $$

(7.4)

and

$$ \Pr ( N(X_{i})\ne 0)=1-\Pr ( N(X_{i})=0)=1-\int _{0}^{\infty }e^{-x\alpha }dB(y). $$

(7.5)

From (7.4) and (7.5), we have

$$ \Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, N(X_{i})\ne 0)\le 1-\int _{0}^{\infty }e^{-x\alpha }dB(y). $$

Since $e^{-x\alpha }>0$ and $\int _{0}^{\infty }|e^{-x\alpha }|dB(y)<\infty$, we get

$$ \lim \limits _{\alpha \rightarrow 0}\Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, N(X_{i})\ne 0)\le 1-\int _{0}^{\infty }\lim \limits _{\alpha \rightarrow 0}e^{-x\alpha }dB(y)=0. $$

Hence $\lim \limits _{\alpha \rightarrow 0}\Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, N(X_{i})\ne 0)=0$. From (7.3), we immediately obtain the following equation:

$$ \lim \limits _{\alpha \rightarrow 0}\hat{B}(x)= \lim \limits _{\alpha \rightarrow 0}\Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x,N(X_{i})=0). $$

(7.6)

According to the multiplication rule of probability, we get

$$ \lim \limits _{\alpha \rightarrow 0}\hat{B}(x)= \lim \limits _{\alpha \rightarrow 0}\Pr (X_{i} \le x|N(X_{i})=0)\Pr (N(X_{i})=0). $$

(7.7)

Because $N(X_{i})$ is independent of $X_{i}$, and $\Pr (N(X_{i})=0)=1-\Pr ( N(X_{i})\ne 0)=1$, then we obtain $\lim \limits _{\alpha \rightarrow 0}\hat{B}(x)= \Pr (X_{i} \le x)=B(x)$. By the Continuity Theorem (see Feller 1971), we have

$$ \lim \limits _{\alpha \rightarrow 0}\hat{B}^{*}(s)=\lim \limits _{\alpha \rightarrow 0}\int _{0}^{\infty }e^{-sx}d\hat{B}(x)=\int _{0}^{\infty }e^{-sx}dB(x)=B^{*}(s). $$

We obtain Lemma 4.3 (1). This completes the proof. $\square$

(2) First we will prove that $\lim \limits _{\theta \rightarrow \infty }\Pr (Y_{ij}\ne 0)=0$. Proof by contradiction is adopted.

Suppose that $\lim \limits _{\theta \rightarrow \infty }\Pr (Y_{ij}\ne 0)\ne 0$, it is readily seen that $\lim \limits _{\theta \rightarrow \infty }E(Y_{ij})>0$ since $Y_{ij}\ge 0$ and $\Pr (Y_{ij}\ne 0)\ne 0$. However, the repair times follow an exponential distribution with rate $\theta$, which means $E(Y_{ij})=\frac{1}{\theta }$, and then $\lim \limits _{\theta \rightarrow \infty }E(Y_{ij})=0$, which conflicts with $\lim \limits _{\theta \rightarrow \infty }E(Y_{ij})>0$. Hence the assumption that $\lim \limits _{\theta \rightarrow \infty }\Pr (Y_{ij}\ne 0)\ne 0$ is not true, and we obtain the fact that $\lim \limits _{\theta \rightarrow \infty }\Pr (Y_{ij}\ne 0)=0$.

According to the property of complementary events, we have $\lim \limits _{\theta \rightarrow \infty }\Pr (Y_{ij}= 0)=1$. On the other hand,

$$ \begin{aligned} \Pr \left( \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0\right)&\;=\int _{0}^{\infty } \sum _{k=0}^{\infty } \Pr \left( \sum _{j=1}^{k}Y_{ij}\ne 0\right) \frac{(x\alpha )^{k} e^{-x\alpha }}{k!}dB(x) \nonumber \\&\;=\int _{0}^{\infty } \sum _{k=0}^{\infty } \left( 1-\Pr \left( \sum _{j=1}^{k}Y_{ij}=0\right) \right) \frac{(x\alpha )^{k} e^{-x\alpha }}{k!}dB(x). \end{aligned}$$

(7.8)

From (7.8), we have

$$ \lim \limits _{\theta \rightarrow \infty }\Pr \left( \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0\right) =\lim \limits _{\theta \rightarrow \infty }\int _{0}^{\infty } \sum _{k=0}^{\infty } \left( 1-\Pr \left( \sum _{j=1}^{k}Y_{ij}=0\right) \right) \frac{(x\alpha )^{k} e^{-x\alpha }}{k!}dB(x). $$

(7.9)

Since $\sum _{k=0}^{\infty } \left( 1-\Pr \left( \sum _{j=1}^{k}Y_{ij}=0\right) \right) \frac{(x\alpha )^{k} e^{-x\alpha }}{k!}>0$ and

$$ \int _{0}^{\infty } \left| \sum _{k=0}^{\infty } \left( 1-\Pr \left( \sum _{j=1}^{k}Y_{ij}=0\right) \right) \frac{(x\gamma )^{k} e^{-x\alpha }}{k!}\right| dB(x)<\infty, $$

Equation (7.9) can be rewritten as

$$ \begin{aligned} \lim \limits _{\theta \rightarrow \infty }\Pr \left( \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0\right)&\;=\int _{0}^{\infty } \lim \limits _{\theta \rightarrow \infty }\sum _{k=0}^{\infty } \left( 1-\Pr \left( \sum _{j=1}^{k}Y_{ij}=0\right) \right) \frac{(x\alpha )^{k} e^{-x\alpha }}{k!}dB(x)\nonumber \\&\;=\int _{0}^{\infty } \sum _{k=0}^{\infty } \left( 1-\lim \limits _{\theta \rightarrow \infty }\Pr \left( \sum _{j=1}^{k}Y_{ij}=0\right) \right) \frac{(x\alpha )^{k} e^{-x\alpha }}{k!}dB(x). \end{aligned}$$

(7.10)

Since $Y_{ij}\ge 0$, $\lim \limits _{\theta \rightarrow \infty }\Pr ( \sum _{j=1}^{k}Y_{ij}=0)=\lim \limits _{\theta \rightarrow \infty }\prod _{i=0}^{k}\Pr ( Y_{ij}=0)=1$. This completes the proof. $\square$

(3) By the definition of distribution function, we have

$$ \lim \limits _{\theta \rightarrow \infty }\hat{B}(x)=\lim \limits _{\theta \rightarrow \infty }\Pr (\hat{X_{i}} \le x)=\lim \limits _{\theta \rightarrow \infty }\Pr \left( X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x\right), $$

(7.11)

which is identical to the following equation:

$$ \begin{aligned} \lim \limits _{\theta \rightarrow \infty }\hat{B}(x)=&\; \lim \limits _{\theta \rightarrow \infty }\Pr \left( X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x,\sum _{j=1}^{N(X_{i})}Y_{ij}=0\right) \nonumber \\&\; + \lim \limits _{\theta \rightarrow \infty }\Pr \left( X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0\right). \end{aligned}$$

(7.12)

Next we prove that $\lim \limits _{\theta \rightarrow \infty }\Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0)=0$. Evidently,

$$ \lim \limits _{\theta \rightarrow \infty }\Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0)\le \lim \limits _{\theta \rightarrow \infty }\Pr ( \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0). $$

(7.13)

From Lemma 4.3 (2), we have

$$ \lim \limits _{\theta \rightarrow \infty }\Pr \left( X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0\right) \le 0, $$

(7.14)

which implies that $\lim \limits _{\theta \rightarrow \infty }\Pr (X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x, \sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0)=0$. Then (7.12) can be rewritten as

$$ \begin{aligned} \lim \limits _{\theta \rightarrow \infty }\hat{B}(x)&\;= \lim \limits _{\theta \rightarrow \infty }\Pr \left( X_{i}+\sum _{j=1}^{N(X_{i})}Y_{ij} \le x,\sum _{j=1}^{N(X_{i})}Y_{ij}=0\right) \nonumber \\&\;= \lim \limits _{\theta \rightarrow \infty }\Pr \left( X_{i} \le x \left| \right. \sum _{j=1}^{N(X_{i})}Y_{ij}=0\right) \Pr \left( \sum _{j=1}^{N(X_{i})}Y_{ij}=0\right). \end{aligned}$$

(7.15)

Since $X_{i}$ is independent of $Y_{ij}, j=1,2,\ldots , N(X_{i})$, Eq. (7.15) becomes

$$ \lim \limits _{\theta \rightarrow \infty }\hat{B}(x) = \Pr (X_{i} \le x)\cdot \lim \limits _{\theta \rightarrow \infty }\Pr \left( \sum _{j=1}^{N(X_{i})}Y_{ij}=0\right). $$

(7.16)

From Lemma 4.3 (2), we know that $\lim \limits _{\theta \rightarrow \infty }\Pr (\sum _{j=1}^{N(X_{i})}Y_{ij}=0)=1- \lim \limits _{\theta \rightarrow \infty }\Pr (\sum _{j=1}^{N(X_{i})}Y_{ij}\ne 0)=1$, and then the following equation holds:

$$ \lim \limits _{\theta \rightarrow \infty }\hat{B}(x)=Pr(X_{i} \le x)=B(X). $$

(7.17)

In virtue of Continuity Theorem (see Feller 1971), the proof is completed. $\square$