Skip to main content

Advertisement

Springer Nature Link
Log in

Assessment of new methods for incorporating contextual variables into efficiency measures: a Monte Carlo simulation

  • Original Paper
  • Published:
Operational Research Aims and scope Submit manuscript

Abstract

The treatment of the contextual variables (Z) has been one of the most controversial topics in the literature on efficiency measurement. Over the last three decades of research, different methods have been developed to incorporate the effect of such variables in the estimation of efficiency measures. However, it is unclear which alternative provides more accurate estimations. The aim of this work is to assess the performance of two recently developed estimators, namely the nonparametric conditional DEA method (Daraio and Simar in J Prod Anal 24(1):93–121, 2005; J Prod Anal 28:13–32, 2007a) and the StoNEZD (Stochastic Non-Smooth Envelopment of Z-variables Data) approach (Johnson and Kuosmanen in J Prod Anal 36(2):219–230, 2011). To do this, we conduct a Monte Carlo experiment using three different data generation processes to test how each model performs under different circumstances. Our results show that the StoNEZD approach outperforms conditional DEA in all the evaluated scenarios.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. Kumbhakar et al. (1991) developed this model for cross-sectional data and, subsequently, Battese and Coelli (1995) adapt the model to the existence of panel data.

  2. A similar strategy was also adopted by Andor and Hesse (2014) to evaluate the performance of several methods for measuring efficiency (DEA, SFA and StoNED), although these authors did not consider the potential influence of contextual variables on efficiency.

  3. We describe the model for the single-output multiple input case since introducing the multi-output context would involve the use of directional distance functions for the case of StoNEZD method (Kuosmanen and Johnson 2017), so the comparison with the conditional DEA model would be more complex.

  4. Kuosmanen and Johnson (2010) show that this problem is equivalent to the standard (output-oriented, variable returns to scale) DEA model when a sign constraint on residuals is incorporated to the formulation (\(\varepsilon_{i}^{CNLS - } \le 0 \forall i\)) and considering the problem subject to shape constraints (monotonicity and convexity).

  5. Several other papers propose using multiplicative error structures when CRS or heteroscedasticity are assumed (Kuosmanen et al. 2015). In the present work we use the additive model because those conditions are not assumed.

  6. Kuosmanen et al. (2015) propose a pseudo-likelihood approach (Fan et al. 1996) or nonparametric kernel deconvolution (Hall and Simar 2002) as alternatives to the method of moments. In this study we use the method of moments due to its easier computation and interpretation. Nevertheless, Andor and Hesse (2014) found similar results for the former, while the latter has not been used in any Monte Carlo simulation to evaluate StoNEZD as far as we know.

  7. Kuosmanen et al. (2015) propose to use the point estimator developed by Jondrow et al. (1982), but it is well-known that it is not a consistent estimator of \(u_{i}\) (Andor and Hesse 2014).

  8. See Greene (1980) for details.

  9. The mean results are similar and are available from the authors upon request.

  10. Cordero et al. 2016 show that the percentage of accuracy of conditional DEA identifying efficient units is around 68–72%.

  11. This additional analysis was included in order to address the suggestion made by an anonymous reviewer.

References

  • Aigner D, Lovell CK, Schmidt P (1977) Formulation and estimation of stochastic frontier production function models. J Econometrics 6(1):21–37

    Google Scholar 

  • Andor M, Hesse F (2014) The StoNED age: the departure into a new era of efficiency analysis? A Monte Carlo comparison of StoNED and the “oldies” (SFA and DEA). J Prod Anal 41(1):85–109

    Google Scholar 

  • Badin L, Daraio C, Simar L (2010) Optimal bandwidth selection for conditional efficiency measures: a data-driven approach. Eur J Oper Res 201:633–640

    Google Scholar 

  • Badin L, Daraio C, Simar L (2012) How to measure the impact of environmental factors in a nonparametric production model. Eur J Oper Res 223(3):818–833

    Google Scholar 

  • Badin L, Daraio C, Simar L (2014) Explaining inefficiency in nonparametric production models: the state of the art. Ann Oper Res 214(1):5–30

    Google Scholar 

  • Badunenko O, Henderson DJ, Kumbhakar SC (2012) When, where and how to perform efficiency estimation. J R Stat Soc A Sta 175(4):863–892

    Google Scholar 

  • Banker RD, Natarajan R (2008) Evaluating contextual variables affecting productivity using data envelopment analysis. Oper Res 56(1):48–58

    Google Scholar 

  • Battese GE, Coelli TJ (1988) Prediction of firm-level technical efficiencies with a generalized frontier production function and panel data. J Econom 38(3):387–399

    Google Scholar 

  • Battese GE, Coelli TJ (1995) A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empir Econ 20:325–332

    Google Scholar 

  • Cazals C, Florens JP, Simar L (2002) Nonparametric frontier estimation: a robust approach. J Econom 106:1–25

    Google Scholar 

  • Chambers RG, Chung YH, Färe R (1996) Benefit and distance functions. J Econ Theory 70(2):407–419

    Google Scholar 

  • Cheng X, Bjorndal E, Bjorndal M (2014) Cost efficiency analysis based on the DEA and StoNED models: case of Norwegian electricity distribution companies. In: 2014 11th international conference on the European energy market (EEM). IEEE, pp 1–6

  • Cherchye L, De Witte K, Ooghe E, Nicaise I (2010) Efficiency and equity in private and public education: a nonparametric comparison. Eur J Oper Res 202:563–573

    Google Scholar 

  • Cordero JM, Pedraja-Chaparro F, Salinas-Jiménez J (2008) Measuring efficiency in education: an analysis of different approaches for incorporating non-discretionary inputs. Appl Econ 40(10):1323–1339

    Google Scholar 

  • Cordero JM, Pedraja F, Santín D (2009) Alternative approaches to include exogenous variables in DEA measures: a comparison using Monte Carlo. Comput Oper Res 36:2699–2706

    Google Scholar 

  • Cordero JM, Alonso-Morán E, Nuño-Solinis R, Orueta JF, Arce RS (2015a) Efficiency assessment of primary care providers: a conditional nonparametric approach. Eur J Oper Res 240(1):235–244

    Google Scholar 

  • Cordero JM, Santín D, Simancas R (2015b) Assessing European primary school performance through a conditional nonparametric model. J Oper Res Soc 68(4):364–376

    Google Scholar 

  • Cordero JM, Polo C, Santín D, Sicilia G (2016) Monte-Carlo comparison of conditional nonparametric methods and traditional approaches to include exogenous variables. Pac Econ Rev 21(4):483–497

    Google Scholar 

  • Daraio C, Simar L (2005) Introducing environmental variables in nonparametric frontier models: a probabilistic approach. J Prod Anal 24(1):93–121

    Google Scholar 

  • Daraio C, Simar L (2006) A robust nonparametric approach to evaluate and explain the performance of mutual funds. Eur J Oper Res 175(1):516–542

    Google Scholar 

  • Daraio C, Simar L (2007a) Conditional nonparametric frontier models for convex and non-convex technologies: a unifying approach. J Prod Anal 28:13–32

    Google Scholar 

  • Daraio C, Simar L (2007b) Advanced robust and nonparametric methods in efficiency analysis. Methodology and applications. Springer, New York

    Google Scholar 

  • Daraio C, Simar L, Wilson PW (2018) Central limit theorems for conditional efficiency measures and tests of the “separability” condition in nonparametric, two-stage models of production. Econom J. https://doi.org/10.1111/ectj.12103

    Article  Google Scholar 

  • De Witte K, Geys B (2013) Citizen coproduction and efficient public good provision: theory and evidence from local public libraries. Eur J Oper Res 224(3):592–602

    Google Scholar 

  • De Witte K, Kortelainen M (2013) What explains the performance of students in a heterogeneous environment? Conditional efficiency estimation with continuous and discrete environmental variables. Appl Econ 45:2401–2412

    Google Scholar 

  • De Witte K, Rogge N, Cherchye L, Van Puyenbroeck T (2013) Economies of scope in research and teaching: a non-parametric investigation. Omega 41(2):305–314

    Google Scholar 

  • Eskelinen J, Kuosmanen T (2013) Intertemporal efficiency analysis of sales teams of a bank: stochastic semi-nonparametric approach. J Bank Finance 37(12):5163–5175

    Google Scholar 

  • Estelle SM, Johnson A, Ruggiero J (2010) Three-stage DEA models for incorporating exogenous inputs. Comput Oper Res 37:1087–1090

    Google Scholar 

  • Fan Y, Li Q, Weersink A (1996) Semiparametric estimation of stochastic production frontier models. J Bus Econ Stat 14(4):460–468

    Google Scholar 

  • Florens J, Simar L, van Keilegom I (2014) Frontier estimation in nonparametric location-scale models. J Econom 178:456–470

    Google Scholar 

  • Greene WH (1980) Maximum likelihood estimation of econometric frontier functions. J Econom 13(1):27–56

    Google Scholar 

  • Haas DA, Murphy FH (2003) Compensating for non-homogeneity in decision-making units in data envelopment analysis. Eur J Oper Res 144(3):530–544

    Google Scholar 

  • Haelermans C, De Witte K (2012) The role of innovations in secondary school performance–Evidence from a conditional efficiency model. Eur J Oper Res 223(2):541–549

  • Halkos G, Tzeremes N (2011a) A conditional nonparametric analysis for measuring the efficiency of regional public healthcare delivery: an application to Greek prefectures. Health Policy 103(1):3–82

    Google Scholar 

  • Halkos G, Tzeremes N (2011b) Modelling regional welfare efficiency applying conditional full frontiers. Spat Econ Anal 6(4):451–471

    Google Scholar 

  • Halkos G, Tzeremes N (2013) A conditional directional distance function approach for measuring regional environmental efficiency: evidence from UK regions. Eur J Oper Res 227:182–189

    Google Scholar 

  • Hall P, Simar L (2002) Estimating a changepoint, boundary, or frontier in the presence of observation error. J Am Stat Assoc 97(458):523–534

    Google Scholar 

  • Hall P, Racine J, Li Q (2004) Cross-validation and the estimation of conditional probability densities. J Am Stat Assoc 99(468):1015–1026

    Google Scholar 

  • Harrison J, Rouse P, Armstrong J (2012) Categorical and continuous non-discretionary variables in data envelopment analysis: a comparison of two single-stage models. J Prod Anal 37(3):261–276

    Google Scholar 

  • Hildreth C (1954) Point estimates of ordinates of concave functions. J Am Stat Assoc 49(267):598–619

    Google Scholar 

  • Huguenin JM (2015) Data envelopment analysis and non-discretionary inputs: how to select the most suitable model using multi-criteria decision analysis. Expert Syst Appl 42(5):2570–2581

    Google Scholar 

  • Jeong SO, Park BU, Simar L (2010) Nonparametric conditional efficiency measures: asymptotic properties. Ann Oper Res 173:105–122

    Google Scholar 

  • Johnson AL, Kuosmanen T (2011) One-stage estimation of the effects of operational conditions and practices on productive performance: asymptotically normal and efficient, root-n consistent StoNEZD method. J Prod Anal 36(2):219–230

    Google Scholar 

  • Kumbhakar SC, Ghosh S, McGuckin JT (1991) A generalized production frontier approach for estimating determinants of inefficiency in US dairy farms. J Bus Econ Stat 9(3):279–286

    Google Scholar 

  • Kuosmanen T (2006) Stochastic nonparametric envelopment of data: combining virtues of SFA and DEA in a unified framework. MTT Discussion Paper No. 3/2006. http://dx.doi.org/10.2139/ssrn.905758

  • Kuosmanen T (2012) Stochastic semi-nonparametric frontier estimation of electricity distribution networks: application of the StoNED method in the Finnish regulatory model. Energy Econ 34:2189–2199

    Google Scholar 

  • Kuosmanen T, Johnson AL (2010) Data envelopment analysis as nonparametric least-squares regression. Oper Res 58:149–160

    Google Scholar 

  • Kuosmanen T, Johnson AL (2017) Modeling joint production of multiple outputs in StoNED: directional distance function approach. Eur J Oper Res 262(2):792–801

    Google Scholar 

  • Kuosmanen T, Saastamoinen A, Sipiläinen T (2013) What is the best practice for benchmark regulation of electricity distribution? Comparison of DEA, SFA and StoNED Methods. Ener Pol 61:740–750

    Google Scholar 

  • Kuosmanen T, Saastamoinen A, Keshvari A, Johnson A, Parmeter C (2014) Tehostamiskannustin sähkön jakeluverkkoyhtiöiden valvontamallissa, Sigma-Hat Economics Oy (in Finnish)

  • Kuosmanen T, Johnson AL, Saastamoinen A (2015) Stochastic nonparametric approach to efficiency analysis: a unified framework. In: Zhu J (ed) Data envelopment analysis. A handbook of models and methods. Springer, New York, pp 191–244

    Google Scholar 

  • Lee CY, Johnson AL, Moreno-Centeno E, Kuosmanen T (2013) A more efficient algorithm for convex nonparametric least squares. Eur J Oper Res 227(2):391–400

    Google Scholar 

  • Li Q, Racine JS (2007) Nonparametric econometrics: theory and practice. Princeton University Press, Princeton

    Google Scholar 

  • Matousek R, Tzeremes NG (2016) CEO compensation and bank efficiency: an application of conditional nonparametric frontiers. Eur J Oper Res 251(1):264–273

    Google Scholar 

  • Mazumder R, Choudhury A, Iyengar G, Sen B (2015) A computational framework for multivariate convex regression and its variants. arXiv preprint arXiv:1509.08165

  • Mekaroonreung M, Johnson AL (2014) A nonparametric method to estimate a technical change effect on marginal abatement costs of US coal power plants. Energy Econ 46:45–55

    Google Scholar 

  • Muñiz MA (2002) Separating managerial inefficiency and external conditions in data envelopment analysis. Eur J Oper Res 143(3):625–643

    Google Scholar 

  • Muñiz M, Paradi J, Ruggiero J, Yang Z (2006) Evaluating alternative DEA models used to control for non-discretionary inputs. Comput Oper Res 33:1173–1183

    Google Scholar 

  • Nieswand M, Seifert S (2018) Environmental factors in frontier estimation-A Monte Carlo analysis. Eur J Oper Res 265(1):133–148

    Google Scholar 

  • Perelman S, Santín D (2009) How to generate regularly behaved production data? A Monte Carlo experimentation on DEA scale efficiency measurement. Eur J Oper Res 199(1):303–310

    Google Scholar 

  • Ray SC (1991) Resource-use efficiency in public schools: a study of connecticut data. Manage Sci 37(12):1620–1628

    Google Scholar 

  • Ruggiero J (1998) Non-discretionary inputs in data envelopment analysis. Eur J Oper Res 111(3):461–469

    Google Scholar 

  • Saastamoinen A, Kuosmanen T (2016) Quality frontier of electricity distribution: supply security, best practices, and underground cabling in Finland. Energy Econ 53:281–292

    Google Scholar 

  • Shephard RW (1970) Theory of cost and production function. Princeton University Press, Princeton

    Google Scholar 

  • Simar L, Wilson PW (2007) Estimation and inference in two-stage, semi parametric models of production processes. J Econom 136:31–64

    Google Scholar 

  • Simar L, Wilson PW (2011) Two-stage DEA: caveat emptor. J Prod Anal 36(2):205–218

    Google Scholar 

  • Simar L, Wilson PW (2015) Statistical approaches for non-parametric frontier models: a guided tour. Int Stat Rev 83(1):77–110

    Google Scholar 

  • Verschelde M, Rogge N (2012) An environment-adjusted evaluation of citizen satisfaction with local police effectiveness: evidence from a conditional data envelopment analysis approach. Eur J Oper Res 223:214–215

    Google Scholar 

  • Vidoli F, Ferrara G (2015) Analyzing Italian citrus sector by semi-nonparametric frontier efficiency models. Empir Econ 49(2):641–658

    Google Scholar 

  • Yagi D, Chen Y, Johnson AL, Kuosmanen T (2018) Shape constrained kernel-weighted least squares: Estimating production functions for Chilean manufacturing industries. J Bus Econ Stat. https://doi.org/10.1080/07350015.2018.1431128

    Article  Google Scholar 

  • Yang H, Pollitt M (2009) Incorporating both undesirable outputs and uncontrollable variables into DEA: the performance of Chinese coal-fired power plants. Eur J Oper Res 197(3):1095–1105

    Google Scholar 

  • Yu C (1998) The effects of exogenous variables in efficiency measurement. A Monte Carlo study. Eur J Oper Res 105:569–580

    Google Scholar 

  • Zhang Y, Bartels R (1998) The effect of sample size on the mean efficiency in DEA with an application to electricity distribution in Australia, Sweden and New Zealand. J Prod Anal 9:187–204

    Google Scholar 

  • Zhang R, Sun K, Delgado MS, Kumbhakar SC (2012) Productivity in China’s high technology industry: regional heterogeneity and R&D. Technol Forecast Soc 79(1):127–141

    Google Scholar 

Download references

Acknowledgements

We are deeply indebted to the participants of the VII International Congress on Efficiency and Productivity (EFIUCO) and the 2016 Asia–Pacific Productivity Conference (APPC) in Tianjin for providing valuable comments that have led to a considerable improvement of earlier versions of this paper. Furthermore, the authors would like to express their gratitude to the Spanish Ministry for Economy and Competitiveness for supporting this research through grant ECO2014-53702-P. Cristina Polo and Jose M. Cordero would also like to acknowledge the support and funds provided by the Extremadura Government (Grants GR15_SEJ015 and IB16171).

Author information

Authors and Affiliations

  1. Department of Economics, University of Extremadura, Av. Elvas s/n, 06006, Badajoz, Spain

    Jose M. Cordero & Cristina Polo

  2. Department of Applied, Political and Public Economics, Complutense University of Madrid, Campus de Somosaguas, 28223, Pozuelo de Alarcón, Madrid, Spain

    Daniel Santín

Authors
  1. Jose M. Cordero
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Cristina Polo
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Daniel Santín
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jose M. Cordero.

Appendix

Appendix

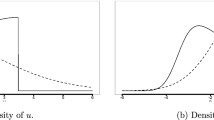
See Fig. 1.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cordero, J.M., Polo, C. & Santín, D. Assessment of new methods for incorporating contextual variables into efficiency measures: a Monte Carlo simulation. Oper Res Int J 20, 2245–2265 (2020). https://doi.org/10.1007/s12351-018-0413-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12351-018-0413-2

Keywords