Skip to main content
Springer Nature Link
Log in

Modelling environmental inefficiency under a quota system

  • Original paper
  • Published:
Operational Research Aims and scope Submit manuscript

Abstract

This paper introduces the methodology necessary to evaluate inefficiency of regulated decision making units that operate under quotas through data envelopment analysis, accounting for both quotas restrictions and negative environmental externalities of production. Three technical inefficiency measures are proposed: inefficiency in the production of marketed output, environmental inefficiency, and inefficiency with quotas. It is then shown how to aggregate these measures in order to obtain indicators of overall performance. The new approach is illustrated through a numerical example that uses real data available for the European Union dairy sector. The results show that considerable differences in inefficiencies could be found when quotas restrictions are accounted for in the model than in the model without quota imposition, indicating that not accounting explicitly for quotas when measuring performance in regulated sectors may lead to a not accurate estimation of firms’ technical inefficiency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. Despite the recent removal of the quota system from the EU dairy sector, as soon as 2016 a new policy to regulate this market with an objective similar to quotas—to reduce the quantity of milk available on the market was introduced. This policy is called ‘milk production reduction scheme’ (European Commission 2016).

  2. The quantities of quotas were divided among producers in each EU member country. The quota transfers and exchanges were allowed with trading rules differing across member countries leading to a large heterogeneity in the implementation of quotas between countries (Ang and Oude Lansink 2016). If the quantities of milk exceeded the quota at country level, the levy needed to be paid by the member country responsible for producing the surplus.

  3. The review of different approaches to modeling environmental efficiency in the agriculture sector is made by Oude Lansink and Wall (2014).

  4. The literature on modeling efficiency of dairy farms without taking into account environmental factors is more extensive including the studies by Mbaga et al. (2003), Alvarez and del Corral (2010), Emvalomatis et al. (2011) or Sauer and Latacz-Lohmann (2015).

  5. Ayres and Kneese (1969) proposed these two same groups when introducing the materials balance to economists.

  6. Bad outputs are introduced as “inputs” in sub-technology T2, something that was criticized in the previous literature on environmental efficiency measurement, as we pointed out in this section. However, Murty and Russell (2018) have recently defended the by-production approach, indicating that there are a lower bound and an upper bound on emission generation for given amounts of emission-generating inputs. The existence of an upper and lower boundary for emissions complicates the modeling of an emission-generating technology, particularly in the study of its disposability and the implied monotonicity properties. Fortunately, as they treat emissions as undesirable by-products, efficiency requires minimization of the production of emissions, conditional on input quantities. Therefore, the attention can be restricted to the study of the properties of the lower bounds on emission generation, which is what is really estimated by the specification of T2.

  7. The reason why we select this particular orientation is twofold. First, from a methodological point of view, it seems natural to resort to the same orientation as used by Murty et al. (2012) since our approach is, in part, an extension of that model. Second, from an empirical point of view, it makes sense to investigate the direct effect of the quota on the inefficiency measure through an output-oriented framework since quota limits the output production and affects it directly.

  8. In model (3) we could substitute \( \theta_{j} \le 1 \) by \( \theta_{j} \) free in the presence of quotas in order to avoid the possibility of infeasibilities when the assessed DMU exceeds the quota constraints. However, if we use that modified model to evaluate a unit that satisfies the quotas, then it is not possible to assure that \( \theta_{j} \le 1 \) for all \( j \) at optimum, which allows to apply the Pareto dominance notion. In this sense, the model that we propose in this paper may be seen as more natural for dealing with this type of context since we do not need to adapt it for units satisfying the quotas and for units exceeding them.

  9. We assume that data observed from the DMUs, inputs and outputs, are affected by the quota restrictions because it is reasonable to think that farms have accounted for quotas in their production plans before producing. Consequently, quotas affect the input mix and thereby influence the pollutant inputs and, implicitly, the bad outputs. However, in our mathematical approach, the constraint associated with the quota appears exclusively in the model related to the standard technology (T1) since good outputs, which are in this case the type of outputs that are regulated, are the only part of the model for measuring standard technical efficiency. Note that, in fact, following Murty et al. (2012), good outputs are not a part of the model associated with the environmental technology T2.

  10. Brännlund et al. (1995) is related to our approach. Brännlund et al. (1995) analyzed the impact of environmental regulation in the Swedish pulp and paper industry on firms’ profit. On one hand, a common feature of Brännlund et al. (1995) and our approach is the way in which regulation is introduced in the model: an upper bound for good outputs. On the other hand, there are two main differences between our model and Brännlund et al. (1995). Firstly, Brännlund et al. (1995) focused on profit inefficiency while our approach focuses on technical inefficiency. In particular, we selected the directional distance function (DDF) for measuring environmental technical inefficiency and defined a suitable DDF to work in the context of by-production (Murty et al., 2012). Secondly, Brännlund et al. (1995) introduced the bad outputs in their model as inputs in one step without distinguishing between non-pollution causing inputs and pollution-generating inputs. In our approach, which is based on the recent by-production model (Murty et al., 2012), the bad outputs are exclusively introduced in sub-technology T2, distinguishing between the two mentioned types of inputs.

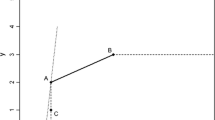
  11. A negative value in the traditional output-oriented directional distance function reflects that the evaluated output bundle is not feasible, i.e. the inputs are not sufficient to produce the output. However, in our approach this interpretation changes and a negative value is associated with producing beyond the quota (see Fig. 1 below).

  12. The data for quotas and milk production is available for the periods 2004/2005, 2006/2007, 2009/2010 and 2012/2013, which corresponds to the years 2005, 2007, 2010 and 2013, respectively, for which the rest of variables is presented.

  13. For Poland and Slovenia the period 2005/2006 was the first year of the application of the quota system, Bulgaria and Romania entered EU in 2007 and their first period of quota data was 2007/2008, while Croatia became EU member in 2013 and its first period of quota data is 2013/2014. So there is no relevant data of quotas for these countries for some of the years of the period analyzed in this paper, hence these countries were excluded from our sample.

  14. The aggregated data concerns specialist dairy farms and cattle-dairying, rearing and fattening combined farms.

  15. Full time corresponds to 1800 annual working hours.

  16. The main environmental issues of dairy sector concern water and air pollution, with the latter being mainly from manure management and enteric fermentation (OECD 2004). Due to the absence of data for water pollution of dairy sector, we restrict our analysis to bad outputs related with greenhouse gas emissions.

  17. As it was mentioned before, our analysis focuses on the delivery quotas. Hence, the variable of milk production is equivalent to quantities of milk delivered to dairies and quota is equivalent to available quota for deliveries.

  18. Usually in the literature concerning agricultural efficiency, the production technology is modeled also including general production costs or purchased feed (see for example, Emvalomatis et al. 2011). However, such data was missing in the datasets used in this study, while in other datasets such data would not be comparable to the remaining variables in our sample.

  19. We apply this test using the data for all analyzed years together instead of performing it year by year to have a large enough sample size. In particular, Li (1996) shows in Monte Carlo simulations that the test performs well for moderate sample sizes. Also, Simar and Zelenyuk (2006) show through Monte Carlo simulations that the test is a reliable tool for moderate dimensions of the DEA model (as measured by the number of inputs and outputs) relative to the sample size. In particular, they concluded that the power of the test is fairly good for the DEA model of two or three inputs and one output for as many as 50 observations in each group. And, for example, for five inputs and one output for 20 observations in each group, they show that the power of the test is quite low. Given the maximum of five dimensions of the DEA model that we have (to estimate good outputs technology we have three inputs and two outputs) and 23 observations of countries in each year, the application of the test on a yearly basis would result in the low power of the test. Hence, we decide to apply the S-Z test for all years together, which results in a considerably larger sample size given the dimensions of the DEA model.

  20. We estimated frontiers separately for each year, which means that we are not able to interpret the results of inefficiency changes over time as improving or worsening with certainty. To interpret the results of inefficiency changes over time with more certainty we would need, for example, to compute inefficiency for all years together (hence, assuming that technology and frontier is not changing over time).

  21. The test (presented in Table 6 and then also in Table 8) was performed for values of inefficiencies for each DMU and not for average values of inefficiencies. The average values of inefficiencies were computed to give an additional glance on countries’ performance over the entire period analyzed.

References

  • Alpay E, Buccola S, Kerkvliet J (2002) Productivity growth and environmental regulation in Mexican and US food manufacturing. Am J Agric Econ 84:887–901

    Google Scholar 

  • Alston J (1981) A note on the effect of non-transferable quotas on supply functions. Rev Mark Agric Econ 49:189–197

    Google Scholar 

  • Alvarez A, del Corral J (2010) Identifying different technologies using a latent class model: extensive versus intensive dairy farms. Eur Rev Agric Econ 37:231–250

    Google Scholar 

  • Alvarez A, Arias C, Orea L (2006) Explaining differences in milk quota values: the role of economic efficiency. Am J Agric Econ 88:182–193

    Google Scholar 

  • Ang F, Oude Lansink A (2016) Decomposing dynamic profit inefficiency of Belgian dairy farms. Working paper

  • Aparicio J, Pastor JT, Ray SC (2013) An overall measure of technical inefficiency at the firm and at the industry level: the ‘lost profit on outlay’. Eur J Oper Res 226:154–162

    Google Scholar 

  • Aparicio J, Kapelko M, Ortiz L, Pastor JT (2017a) Production under a quota system: an extension of the weighted additive model to assess technical efficiency. INFOR: Inf Syst Oper Res 55:227–242

    Google Scholar 

  • Aparicio J, Barbero J, Kapelko M, Pastor JT, Zofío JL (2017b) Testing the consistency and feasibility of the standard Malmquist–Luenberger index: environmental productivity in world air emissions. J Environ Manage 196:148–160

    Google Scholar 

  • Areal FJ, Tiffin R, Balcombe KG (2012a) Farm technical efficiency under a tradable milk quota system. J Dairy Sci 95:50–62

    Google Scholar 

  • Areal FJ, Tiffin R, Balcombe KG (2012b) Provision of environmental output within a multi-output distance function approach. Ecol Econ 78:47–54

    Google Scholar 

  • Ayres RU, Kneese AV (1969) Production, consumption and externalities. Am Econ Rev 59(7):282–297

    Google Scholar 

  • Boots M, Oude Lansink A, Peerlings J (1997) Efficiency loss due to distortions in Dutch milk quota trade. Eur Rev Agric Econ 24:31–46

    Google Scholar 

  • Bouamra-Mechemache Z, Jongeneel R, Réquillart V (2008) Impact of a gradual increase in milk quotas on the EU dairy sector. Eur Rev Agric Econ 35:461–491

    Google Scholar 

  • Brännlund R, Färe R, Grosskopf S (1995) Environmental regulation and profitability: an application to Swedish pulp and paper mills. Environ Resour Econ 6(1):23–36

    Google Scholar 

  • Burrell A (1985) Price uncertainty under EC milk quotas. Eur Rev Agric Econ 12:335–350

    Google Scholar 

  • Cazals C, Florens JP, Simar L (2002) Nonparametric frontier estimation: a robust approach. J Econ 106:1–25

    Google Scholar 

  • Chambers RG, Serra T, Oude Lansink A (2014) On the pricing of undesirable state-contingent outputs. Eur Rev Agric Econ 41:485–509

    Google Scholar 

  • Colman D (2000) Inefficiencies in the UK milk quota system. Food Policy 25:1–16

    Google Scholar 

  • Dakpo KH, Jeanneaux P, Latruffe L (2016) Modeling pollution-generating technologies in performance benchmarking: recent developments, limits and future prospects in the nonparametric framework. Eur J Oper Res 250:347–359

    Google Scholar 

  • Dakpo KH, Jeanneaux P, Latruffe L (2017) Greenhouse gas emissions and efficiency in French sheep meat farming: a nonparametric framework of pollution adjusted technologies. Eur Rev Agric Econ 44:33–65

    Google Scholar 

  • Dyson RG, Allen R, Camanho AS, Podinovski VV, Sarrico CS, Shale EA (2001) Pitfalls and protocols in DEA. Eur J Oper Res 132(2):245–259

    Google Scholar 

  • Emvalomatis G, Stefanou SE, Oude Lansink A (2011) A reduced-form model for dynamic efficiency measurement: application to dairy farms in Germany and the Netherlands. Am J Agric Econ 93:161–174

    Google Scholar 

  • European Commission (2016) Policy instruments for the dairy sector. https://ec.europa.eu/agriculture/milk/policy-instruments_en. Accessed 15 Aug 2017

  • European Commission (2017) EU Milk Market Observatory. EU milk quota figures. https://ec.europa.eu/agriculture/market-observatory/milk/latest-statistics/productions-stocks_en. Accessed 10 July 2017

  • European Parliament (2016) Precision agriculture and the future of farming in Europe. http://www.europarl.europa.eu/RegData/etudes/STUD/2016/581892/EPRS_STU(2016)581892_EN.pdf. Accessed 4 Jan 2018

  • Eurostat (2017) Agricultural Statistics. http://ec.europa.eu/eurostat/web/agriculture. Accessed 10 July 2017

  • Färe R, Grosskopf S (2003) Nonparametric productivity analysis with undesirable outputs: comment. Am J Agric Econ 85:1070–1074

    Google Scholar 

  • Färe R, Grosskopf S (2004) Modeling undesirable factors in efficiency evaluation: comment. Eur J Oper Res 157:242–245

    Google Scholar 

  • Färe R, Grosskopf S, Lovell CAK (1985) The measurement of efficiency of production. Kluwer-Nijhoff, Boston

    Google Scholar 

  • Färe R, Grosskopf S, Pasurka C (1986) Effects on relative efficiency in electric power generation due to environmental controls. Resour Energy 8:167–184

    Google Scholar 

  • Färe R, Grosskopf S, Hernandez-Sancho F (2004) Environmental performance: an index number approach. Resour Energy Econ 26:343–352

    Google Scholar 

  • Ferjani A (2011) Environmental regulation and productivity: a data envelopment analysis for Swiss dairy farms. Agric Econ Rev 12:45–55

    Google Scholar 

  • Førsund FR (2009) Good modeling of bad outputs: pollution and multiple-output production. Int Rev Environ Resour Econ 3:1–38

    Google Scholar 

  • Førsund FR (2018) Multi-equation modelling of desirable and undesirable outputs satisfying the materials balance. Empir Econ 54(1):67–99

    Google Scholar 

  • Frahan De, Baudry A, de Blander R, Polome P, Howitt R (2011) Dairy farms without quotas in Belgium: estimation and simulation with a flexible cost function. Eur Rev Agric Econ 38:469–495

    Google Scholar 

  • Frisch R (1965) Theory of production. D. Reidel Publishing Company, Dordrecht

    Google Scholar 

  • Fulginiti L, Perrin R (1993) The theory and measurement of producer response under quotas. Rev Econ Stat 75:97–106

    Google Scholar 

  • Hailu A (2003) Nonparametric productivity analysis with undesirable outputs: reply. Am J Agric Econ 85:1075–1077

    Google Scholar 

  • Hailu A, Veeman TS (2000) Environmentally sensitive productivity analysis of the Canadian pulp and paper industry, 1959–1994: an input distance function approach. J Environ Econ Manag 40:251–274

    Google Scholar 

  • Hampf B, Rødseth KL (2015) Carbon dioxide emission standards for US power plants: an efficiency analysis perspective. Energy Econ 50:140–153

    Google Scholar 

  • Huettel S, Jongeneel R (2011) How has the EU milk quota affected patterns of herd-size change? Eur Rev Agric Econ 38:497–527

    Google Scholar 

  • Jaraitė J, di Maria C (2012) Efficiency, productivity and environmental policy: a case study of power generation in the EU. Energy Econ 34:1557–1568

    Google Scholar 

  • Kapelko M, Oude Lansink A, Stefanou S (2015) Effect of food regulation on the Spanish food processing industry: a dynamic productivity analysis. PLoS ONE 10(6):e0128217. https://doi.org/10.1371/journal.pone.0128217

    Article  Google Scholar 

  • Li Q (1996) Nonparametric testing of closeness between two unknown distribution functions. Econ Rev 15:261–274

    Google Scholar 

  • Lozano S (2015) A joint-inputs network DEA approach to production and pollution-generating technologies. Expert Syst Appl 42:7960–7968

    Google Scholar 

  • Mahlberg B, Sahoo BK (2011) Radial and non-radial decomposition of Luenberger productivity indicator with an illustrative application. Int J Prod Econ 131:721–726

    Google Scholar 

  • Mbaga MD, Romain R, Larue B, Lebel L (2003) Assessing technical efficiency of Québec dairy farms. Can J Agric Econ 51:121–137

    Google Scholar 

  • Murty S (2010) Externalities and fundamental nonconvexities: a reconciliation of approaches to general equilibrium externality modeling and implications for decentralization. J Econ Theory 145:331–353

    Google Scholar 

  • Murty S, Russell RR (2002) On modeling pollution generating technologies. Discussion Papers Series. Riverside: University of California, Department of Economics

  • Murty S, Russell RR (2018) Modeling emission-generating technologies: reconciliation of axiomatic and by-production approaches. Empir Econ 54(1):7–30

    Google Scholar 

  • Murty S, Russell RR, Levkoff SB (2012) On modeling pollution-generating technologies. J Environ Econ Manag 64:117–135

    Google Scholar 

  • Naylor EL (1987) EEC milk quotas. Agric Adm Ext 24:177–185

    Google Scholar 

  • OECD (2004) Agriculture, Trade and the Environment: The Dairy Sector. http://www.oecd.org/tad/sustainable-agriculture/agriculturetradeandtheenvironmentthedairysector.htm. Accessed 15 Aug 2017

  • Orea L, Wall A (2017) A parametric approach to estimating eco-efficiency. J Agric Econ 68(3):901–907

    Google Scholar 

  • Oude Lansink A, Wall A (2014) Frontier models for evaluating environmental efficiency: an overview. Econ Bus Lett 3:43–50

    Google Scholar 

  • Pérez Urdiales M, Oude Lansink A, Wall A (2016) Eco-efficiency among dairy farmers: the importance of socio-economic characteristics and farmer attitudes. Environ Resour Econ 64:559–574

    Google Scholar 

  • Reinhard S, Lovell CAK, Thijssen GJ (1999) Econometric estimation of technical and environmental efficiency: an application to Dutch dairy farms. Am J Agric Econ 81:44–60

    Google Scholar 

  • Reinhard S, Lovell CAK, Thijssen GJ (2000) Environmental efficiency with multiple environmentally detrimental variables; estimated with SFA and DEA. Eur J Oper Res 121:287–303

    Google Scholar 

  • Sauer J (2010) Deregulation and dairy production systems: a Bayesian distance function approach. J Prod Anal 34:213–237

    Google Scholar 

  • Sauer J, Latacz-Lohmann U (2015) Investment, technical change and efficiency: empirical evidence from German dairy production. Eur Rev Agric Econ 42:151–175

    Google Scholar 

  • Seiford LM, Zhu J (2002) Modeling undesirable factors in efficiency evaluation. Eur J Oper Res 142:16–20

    Google Scholar 

  • Seiford LM, Zhu J (2005) A response to comments on modeling undesirable factors in efficiency evaluation. Eur J Oper Res 161:579–581

    Google Scholar 

  • Serra T, Chambers RG, Oude Lansink A (2014) Measuring technical and environmental efficiency in a state-contingent technology. Eur J Oper Res 236:706–717

    Google Scholar 

  • Shortall OK, Barnes AP (2013) Greenhouse gas emissions and the technical efficiency of dairy farmers. Ecol Ind 29:478–488

    Google Scholar 

  • Simar L, Zelenyuk V (2006) On testing equality of distributions of technical efficiency scores. Econ Rev 25(4):497–522

    Google Scholar 

  • Simar L, Vanhems A, Wilson PW (2012) Statistical inference for DEA estimators of directional distances. Eur J Oper Res 220:853–864

    Google Scholar 

  • Steeneveld W, Tauer LW, Hogeveen H, Oude Lansink A (2012) Comparing technical efficiency of farms with an automatic milking system and a conventional milking system. J Dairy Sci 95:7391–7398

    Google Scholar 

  • Vlontzos G, Niavis S, Manos B (2014) A DEA approach for estimating the agricultural energy and environmental efficiency of EU countries. Renew Sustain Energy Rev 40:91–96

    Google Scholar 

  • Zhao Z (2017) Measurement of production efficiency and environmental efficiency in China’s province level: a by-production approach. Environ Econ Policy Stud 19:735–759

    Google Scholar 

  • Zofío JL, Prieto AM (2001) Environmental efficiency and regulatory standards: the case of CO2 emissions from OECD industries. Resour Energy Econ 23:63–83

    Google Scholar 

Download references

Acknowledgements

The authors are grateful to the National Science Centre in Poland (grant number 2016/23/B/HS4/03398) and the Spanish Ministry for Economy and Competitiveness (Ministerio de Economia, Industria y Competitividad), the State Research Agency (Agencia Estatal de Investigacion) and the European Regional Development Fund (Fondo Europeo de Desarrollo Regional) under grant MTM2016-79765-P (AEI/FEDER, UE) for providing financial support for this article. The calculations of adapted Li test were made at the Wroclaw Centre for Networking and Supercomputing (www.wcss.wroc.pl), Grant No. 286.

Author information

Authors and Affiliations

  1. Center of Operations Research (CIO), Miguel Hernandez University of Elche (UMH), Avda. de la Universidad s/n, 03202, Elche, Alicante, Spain

    Juan Aparicio & Lidia Ortiz

  2. Institute of Applied Mathematics, Department of Logistics, Wrocław University of Economics, Wrocław, Poland

    Magdalena Kapelko

Authors
  1. Juan Aparicio
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Magdalena Kapelko
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Lidia Ortiz
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Juan Aparicio.

Ethics declarations

Conflict of interest

The authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aparicio, J., Kapelko, M. & Ortiz, L. Modelling environmental inefficiency under a quota system. Oper Res Int J 21, 1097–1124 (2021). https://doi.org/10.1007/s12351-019-00487-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12351-019-00487-z

Keywords