Skip to main content
Springer Nature Link
Log in

A new repair model and its optimization for cold standby system

  • Original paper
  • Published:
Operational Research Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

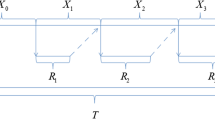
In this paper, we propose a new repair model for a cold standby system, which consists of two components and one repairman. It is assumed that the consecutive working time follows decreasing geometric process after repair, and the repair time interval is a constant for component 1. For component 2 (standby component), the failure process during working time follows Generalized Polya Process, which is a generalized version of the nonhomogeneous Poisson process. Component 2 is rectified by Generalized Polya Process repair when it fails. The repair time of component 2 is assumed to be negligible. Component 1 is assumed to have priority in use. The long-run average cost rate function of the system is deduced based on the failure number of component 1. Moreover, the optimal replacement policy of model is established by minimizing the long-run average cost rate function theoretically, which proves the existence and uniqueness of the optimal replacement policy. Numerical examples are provided to verify the effectiveness of the proposed approaches. Sensitivity analysis are conducted to illustrate the influence of parameters under the optimal replacement policy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Avenab T (2008) A minimal repair replacement model with two types of failure and a safety constraint. Eur J Oper Res 188(2):506–515

    Article  Google Scholar 

  • Barlow R, Hunter L (1960) Optimum preventive maintenance policies. Oper Res 8(1):90–100

    Article  Google Scholar 

  • Braun WJ, Li W, Zhao YQ (2005) Properties of the geometric and related processes. Naval Res Logist (NRL) 52(7):607–616

    Article  Google Scholar 

  • Brown M, Proschan F (1983) Imperfect repair. J Appl Probab 20(4):851–859

    Article  Google Scholar 

  • Berrade M, Scarf PA, Cavalcante CAV (2017) A study of postponed replacement in a delay time model. Reliab Eng Syst Saf 168:70–79

    Article  Google Scholar 

  • Cha JH (2014) Characterization of the generalized polya process and its applications. Adv Appl Probab 46(4):1148–1171

    Article  Google Scholar 

  • Cha JH, Finkelstein M (2009) On a terminating shock process with independent wear increments. J Appl Probab 46(2):353–362

    Article  Google Scholar 

  • Cha JH, Finkelstein M (2011) On new classes of extreme shock models and some generalizations. J Appl Probab 48(1):258–270

    Article  Google Scholar 

  • Cha JH, Finkelstein M (2018) On information-based residual lifetime in survival models with delayed failures. Stat Probab Lett 137:209–216

    Article  Google Scholar 

  • Chan JS, Yu PL, Lam Y, Ho AP (2006) Modelling SARS data using threshold geometric process. Stat Med 25(11):1826–1839

    Article  Google Scholar 

  • Chen M, Zhao XF, Nakagawa T (2019) Replacement policies with general models. Ann Oper Res 277(1):47–61

    Article  Google Scholar 

  • Finkelstein MS (1993) A scale model of general repair. Microelectron Reliab 33(1):41–44

    Article  Google Scholar 

  • Ito K, Zhao XF, Nakagawa T (2017) Random number of units for k-out-of-n systems. Appl Math Model 45:563–572

    Article  Google Scholar 

  • Jaturonnateeaba J (2006) Optimal preventive maintenance of leased equipment with corrective minimal repairs. Eur J Oper Res 174(1):201–215

    Article  Google Scholar 

  • Lam Y (1988a) Geometric processes and replacement problem. Acta Math Appl Sin 4:366–377

    Article  Google Scholar 

  • Lam Y (1988b) A note on the optimal replacement problem. Adv Appl Probab 20(2):479–482

    Article  Google Scholar 

  • Lam Y (2007) The geometric process and its applications. World Scientific, Singapore

    Book  Google Scholar 

  • Lee H, Cha JH (2016) New stochastic models for preventive maintenance and maintenance optimization. Eur J Oper Res 255(1):80–90

    Article  Google Scholar 

  • Levitin G, Finkelstein M (2019) Optimal loading of elements in series systems exposed to external shocks. Reliab Eng Syst Saf. https://doi.org/10.1016/j.ress.2017.08.009

    Article  Google Scholar 

  • Levitin G, Finkelstein M, Dai Y (2018) Optimizing availability of heterogeneous standby systems exposed to shocks. Reliab Eng Syst Saf 170:137–145

    Article  Google Scholar 

  • Lim JH, Qu J, Zuo MJ, Soares CG (2016) Age replacement policy based on imperfect repair with random probability. Reliab Eng Syst Saf 149:24–33

    Article  Google Scholar 

  • Nakagawa T (1986) Periodic and sequential preventive maintenance policies. J Appl Probab 23(2):536–542

    Article  Google Scholar 

  • Ross SM (1996) Stochastic processes, 2nd edn. Wiley, New York

    Google Scholar 

  • Sheu SH, Li SH (2012) A generalised maintenance policy with age-dependent minimal repair cost for a system subject to shocks under periodic overhaul. Int J Syst Sci 43(6):1007–1013

    Article  Google Scholar 

  • Sheu SH, Chen YL, Chang CC, Zhang ZG (2016) A note on a two variable block replacement policy for a system subject to non-homogeneous pure birth shocks. Appl Math Model 40:3703–3712

    Article  Google Scholar 

  • Smith WL, Leadbetter MR (1963) On the renewal function for the Weibull distribution. Technometrics 5(3):393–396

    Article  Google Scholar 

  • Stadje W, Zuckerman D (1990) Optimal strategies for some repair replacement models. Adv Appl Probab 22(3):641–656

    Article  Google Scholar 

  • Tsai HN, Sheu SH, Zhang ZG (2017) A trivariate optimal replacement policy for a deteriorating system based on cumulative damage and inspections. Reliab Eng Syst Saf 160:74–88

    Article  Google Scholar 

  • Wang GJ, Zhang YL (2011) A bivariate optimal replacement policy for a cold standby repairable system with preventive repair. Appl Math Comput 218(7):3158–3165

    Google Scholar 

  • Wang GJ, Zhang YL (2016) Optimal replacement policy for a two-dissimilar-component cold standby system with different repair actions. Int J Syst Sci 47(5):1021–1031

    Article  Google Scholar 

  • Wu S (2018) Doubly geometric processes and applications. J Oper Res Soc 69(1):66–77

    Article  Google Scholar 

  • Wu S, Wang G (2017) The semi-geometric process and some properties. IMA J Manag Math 29(2):229–245

    Article  Google Scholar 

  • Zhang YL (1994) A bivariate optimal replacement policy for a repairable system. J Appl Probab 31(4):1123–1127

    Article  Google Scholar 

  • Zhang YL, Wang GJ (2007) A deteriorating cold standby repairable system with priority in use. Eur J Oper Res 183(1):278–295

    Article  Google Scholar 

  • Zhang YL, Wang GJ (2009) A geometric process repair model for a repairable cold standby system with priority in use and repair. Reliab Eng Syst Saf 94(11):1782–1787

    Article  Google Scholar 

  • Zhang YL, Wang GJ (2016) An extended geometric process repair model for a cold standby repairable system with imperfect delayed repair. Int J Syst Sci Oper Logist 3(3):163–175

    Google Scholar 

  • Zhao XF, Nakagawa T (2012) Optimization problems of replacement first or last in reliability theory. Eur J Oper Res 223:141–149

    Article  Google Scholar 

  • Zhao XF, Al-Khalifa KN, Nakagawa T (2015) Approximate methods for optimal replacement, maintenance, and inspection policies. Reliab Eng Syst Saf 144:68–73

    Article  Google Scholar 

  • Zhao XF, Al-Khalifa KN, Hamouda AM, Nakagawa T (2017a) Age replacement models: a summary with new perspectives and methods. Reliab Eng Syst Saf 161:95–105

    Article  Google Scholar 

  • Zhao XF, Qian CH, Nakagawa T (2017b) Comparisons of replacement policies with periodic times and repair numbers. Reliab Eng Syst Saf 168:161–170

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by National Natural Science Foundation of China under Grant number [61573014] and the Fundamental Research Funds for the Central Universities of China under Grant number [JB180702]. The authors would like to thank the editor and the anonymous referees for the valuable suggestions that improved the quality of this paper.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xidian University, Xi’an, 710071, China

    Junyuan Wang & Jimin Ye

Authors
  1. Junyuan Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jimin Ye
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jimin Ye.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by National Natural Science Foundation of China [Grant number 61573014] and the Fundamental Research Funds for the Central Universities of China [Grant Number JB180702].

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, J., Ye, J. A new repair model and its optimization for cold standby system. Oper Res Int J 22, 105–122 (2022). https://doi.org/10.1007/s12351-020-00545-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12351-020-00545-x

Keywords