Appendix 1
$$\begin{aligned} B_0 & = {} \left( {\begin{array}{*{20}c} O &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {I \otimes D_1^{(A)} } &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad \ddots &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {I \otimes D_1^{(A)} } \\ \end{array}} \right) ,\\ B_2 & = {} \left( {\begin{array}{*{20}c} O &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {T^0 \otimes I} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {\gamma \otimes T^0 \otimes I} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad \ddots &{}\quad {\ddots } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {\gamma \otimes T^0 \otimes I} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\mathcal {U}} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\mathcal {V}} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \ddots &{}\quad {\ddots } &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\mathcal {V}} &{}\quad {O} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {V}}_0 } &{}\quad {O} &{}\quad {O} \\ \end{array}} \right) ,\\ B_{10} & = {} \left( {\begin{array}{*{20}c} O &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {T^0 \otimes I} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {T^0 \otimes I} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad \ddots &{}\quad {\ddots } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad { T^0 \otimes I} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \tilde{\mathcal{U}} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \tilde{\mathcal{V}} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \ddots &{}\quad {\ddots } &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \tilde{\mathcal{V}} &{}\quad {O} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{\mathcal{V}}_0 } &{}\quad {O} &{}\quad {O} \\ \end{array}} \right) ,\\ B_1 & = {} \left( {\begin{array}{*{20}c} {{\mathcal {G}}_0 } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}'_0 } \\ {{\mathcal {F}}_0 } &{}\quad {{\mathcal {G}}_1 } &{}\quad {{\mathcal {H}}_{S - 1} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}^* } \\ \vdots &{}\quad {} &{}\quad \ddots &{}\quad \ddots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \vdots \\ {{\mathcal {F}}_0 } &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}_s } &{}\quad {{\mathcal {H}}_{S - s} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}^* } \\ {{\mathcal {F}} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}_{s + 1} } &{}\quad {{\mathcal {H}}_{S - (s + 1)} } &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}^{**} } \\ \vdots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \ddots &{}\quad \ddots &{}\quad {} &{}\quad \vdots \\ {{\mathcal {F}} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}_{S - 1} } &{}\quad {{\mathcal {H}}_1 } &{}\quad {{\mathcal {G}}^{**} } \\ {{\mathcal {F}} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}_S } &{}\quad {{\mathcal {G}}^{**} } \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}_{S^* } } \\ \end{array}} \right) , \\ \end{aligned}$$
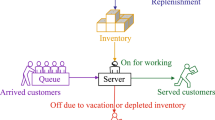
with \(B_0, B_1, B_2\) represent the arrival of customers, transitions within the states and service completion of customers respectively. In \(B_0\), the system has n customers move to \(n+1\) customers without change of inventory level, for \(n \ge 1\). Each matrices is of order \([(2S-s+1)r+1]m_2m_1\).
$$\begin{aligned} B_{00} & = {} \left( {\begin{array}{*{20}c} {{\mathcal {G}}_0 } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}'_0 } \\ {{\mathcal {F}}_0 } &{}\quad {\tilde{\mathcal{G}}_1 } &{}\quad {{\mathcal {H}}_{S - 1} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}^* } \\ \vdots &{}\quad {} &{}\quad \ddots &{}\quad \ddots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \vdots \\ {{\mathcal {F}}_0 } &{}\quad {} &{}\quad {} &{}\quad {\tilde{\mathcal{G}}_s } &{}\quad {{\mathcal {H}}_{S - s} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}^* } \\ {{\mathcal {F}} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{\mathcal{G}}_{s + 1} } &{}\quad {{\mathcal {H}}_{S - (s + 1)} } &{}\quad {} &{}\quad {} &{}\quad {{\mathcal {G}}^{**} } \\ \vdots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \ddots &{}\quad \ddots &{}\quad {} &{}\quad \vdots \\ {{\mathcal {F}} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{\mathcal{G}}_{S - 1} } &{}\quad {{\mathcal {H}}_1 } &{}\quad {{\mathcal {G}}^{**} } \\ {{\mathcal {F}} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{\mathcal{G}}_S } &{}\quad {{\mathcal {G}}^{**} } \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{\mathcal{G}}_{S^* } } \\ \end{array}} \right) , \\ B_{01} & = {} \left( {\begin{array}{*{20}c} O &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {\gamma \otimes I \otimes D_1^{(A)} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad \ddots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {\gamma \otimes I \otimes D_1^{(A)} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad L &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \ddots &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad L &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\gamma \otimes I \otimes D_1^{(A)} } \\ \end{array}} \right) \end{aligned}$$
(sub-matrices are given in “Appendix 2”).
Appendix 2
$$\begin{aligned} {\mathcal {U}} & = {} \left( \begin{array}{l} \gamma \otimes T^0 \otimes I \\ \gamma \otimes T^0 \otimes I \\ \end{array} \right) ,{\mathcal {V}} = \left( {\begin{array}{*{20}c} {\gamma \otimes T^0 \otimes I} &{}\quad \\ &{}\quad {\gamma \otimes T^0 \otimes I} \\ \end{array}} \right) ,{\mathcal {V}}_0 = \left( {\begin{array}{*{20}c} {\gamma \otimes T^0 \otimes I} &{}\quad O \\ \end{array}} \right) \\ \tilde{\mathcal{U}} & = {} \left( \begin{array}{l} T^0 \otimes I \\ T^0 \otimes I \\ \end{array} \right) ,\tilde{\mathcal{V}} = \left( {\begin{array}{*{20}c} { T^0 \otimes I} &{}\quad \\ &{}\quad { T^0 \otimes I} \\ \end{array}} \right) ,\tilde{\mathcal{V}}_0 = \left( {\begin{array}{*{20}c} { T^0 \otimes I} &{}\quad O \\ \end{array}} \right) \\ {\mathcal {F}}_0 & = {} \alpha e \otimes I, {\mathcal {F}} = \left( \begin{array}{l} \alpha e \otimes I \\ \alpha e \otimes I \\ \end{array} \right) , {\mathcal {G}}_0 = D_0^{(R)} \oplus D^{(A)} ,{\mathcal {G}}'_0 = \gamma \otimes D_1^{(R)} \otimes I,\\ {\mathcal {H}}_i & = {} i\beta I,\text { for } S - s + 1 \le i \le S - 1,{\mathcal {H}}_{S-s} = \left( {\begin{array}{*{20}c} O &{} {(S-s)\beta I} \\ \end{array}} \right) , \\ {\mathcal {H}}_i & = {} \left( {\begin{array}{*{20}c} {i\beta I} &{}\quad {} \\ {} &{}\quad {i\beta I} \\ \end{array}} \right) ,\text { for }1 \le i \le S - s - 1, {\mathcal {G}}^* = I \otimes D_1^{(R)} \otimes I,{\mathcal {G}}^{**} = \left( \begin{array}{l} O \\ I \otimes D_1^{(R)} \otimes I \\ \end{array} \right) , \\ {\mathcal {G}}_i & = {} T \oplus D_0^{(R)} \oplus D_0^{(A)} - (\alpha + (S - i)\beta )I, \text { for }1 \le i \le s, \\ {\mathcal {G}}_i & = {} \left( {\begin{array}{*{20}c} {{\mathcal {G}}_i^0 } &{}\quad {} \\ {} &{}\quad {{\mathcal {G}}_i^1 } \\ \end{array}} \right) , \text { for }s + 1 \le i \le S \\ {\mathcal {G}}_i^0 & = {} T \oplus D_{}^{(R)} \oplus D_0^{(A)} - (\alpha + (S - i)\beta )I, \\ {\mathcal {G}}_i^1 & = {} T \oplus D_0^{(R)} \oplus D_0^{(A)} - (\alpha + (S - i)\beta )I, \\ {\mathcal {G}}_{S^*} & = {} T \oplus D^{(R)} \oplus D_0^{(A)},\\ \tilde{\mathcal{G}}_i & = {} D_0^{(R)} \oplus D_0^{(A)} - (\alpha + (S - i)\beta )I, \text { for }1 \le i \le s, \\ \tilde{\mathcal{G}}_i & = {} \left( {\begin{array}{*{20}c} {\tilde{\mathcal{G}}_i^0 } &{} {} \\ {} &{} {\tilde{\mathcal{G}}_i^1 } \\ \end{array}} \right) , \text { for }s + 1 \le i \le S \\ \tilde{\mathcal{G}}_i^0 & = {} D_{}^{(R)} \oplus D_0^{(A)} - (\alpha + (S - i)\beta )I, \\ \tilde{\mathcal{G}}_i^1 & = {} D_0^{(R)} \oplus D_0^{(A)} - (\alpha + (S - i)\beta )I, \\ \tilde{\mathcal{G}}_{S^*} & = {} D^{(R)} \oplus D_0^{(A)},\\ L & = {} \left( {\begin{array}{*{20}c} {\gamma \otimes I \otimes D_1^{(A)} } &{}\quad {} \\ {} &{}\quad {\gamma \otimes I \otimes D_1^{(A)} } \\ \end{array}} \right) . \end{aligned}$$
Appendix 3
$$\begin{aligned} A_0 & = {} \left( {\begin{array}{*{20}c} O &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {\lambda I } &{}\quad {} &{}\quad {} \\ {} &{}\quad {} &{}\quad \ddots &{}\quad {} \\ {} &{}\quad {} &{}\quad {} &{}\quad {\lambda I } \\ \end{array}} \right) , A_2 = \left( {\begin{array}{*{20}c} O &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} {} \\ {\mu I} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} \\ {} &{}\quad {} \ddots &{}\quad {\ddots } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} {} \\ {} &{}\quad {} {} &{}\quad {\mu I} &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} {} \\ {} &{}\quad {} &{}\quad {} {} &{}\quad U &{}\quad {O} &{}\quad {} &{}\quad {} &{}\quad {} {} \\ {} &{}\quad {} &{}\quad {} {} &{}\quad {} &{}\quad V &{}\quad {O} &{}\quad {} {} {} \\ {} &{}\quad {} &{}\quad {} {} &{}\quad {} &{}\quad {} &{}\quad \ddots &{}\quad {\ddots } {} {} \\ {} &{}\quad {} &{}\quad {} {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad V &{}\quad {O} &{}\quad {} \\ {} &{}\quad {} &{}\quad {} {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad V_0 &{}\quad {O} &{}\quad {O} \\ \end{array}} \right) ,\\ A_1 & = {} \left( {\begin{array}{*{20}c} {D_0^{(R)} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {D_1^{(R)} } \\ {\alpha I } &{}\quad {G_1 } &{}\quad {H_{S - 1} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {D_1^{(R)} } \\ \vdots &{}\quad {} &{}\quad \ddots &{}\quad \ddots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \vdots \\ {\alpha I } &{}\quad {} &{}\quad {} &{}\quad {G_s } &{}\quad {H_{S - s} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {D_1^{(R)} } \\ {F } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {G_{s + 1} } &{}\quad {H_{S - (s + 1)} } &{}\quad {} &{}\quad {} &{}\quad {G^{*} } \\ \vdots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \ddots &{}\quad \ddots &{}\quad {} &{}\quad \vdots \\ {F} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {G_{S - 1} } &{}\quad {H_1 } &{}\quad {G^{*} } \\ {F} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {G_S } &{}\quad {G^{*} } \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {G_{S^* } } \\ \end{array}} \right) , \\ A_{00} & = {} \left( {\begin{array}{*{20}c} {D_0^{(R)} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {D_1^{(R)} } \\ {\alpha I } &{}\quad {\tilde{G}_1 } &{}\quad {H_{S - 1} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {D_1^{(R)} } \\ \vdots &{}\quad {} &{}\quad \ddots &{}\quad \ddots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \vdots \\ {\alpha I } &{}\quad {} &{}\quad {} &{}\quad {\tilde{G}_s } &{}\quad {H_{S - s} } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {D_1^{(R)} } \\ {F } &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{G}_{s + 1} } &{}\quad {H_{S - (s + 1)} } &{}\quad {} &{}\quad {} &{}\quad {G^{*} } \\ \vdots &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad \ddots &{}\quad \ddots &{}\quad {} &{}\quad \vdots \\ {F} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{G}_{S - 1} } &{}\quad {H_1 } &{}\quad {G^{*} } \\ {F} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{G}_S } &{}\quad {G^{*} } \\ {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {} &{}\quad {\tilde{G}_{S^* } } \\ \end{array}} \right) \end{aligned}$$
(sub-matrices are given “Appendix 4”).
Appendix 4
$$\begin{aligned} U & = {} \left( \begin{array}{l} \mu I \\ \mu I \\ \end{array} \right) ,V = \left( {\begin{array}{*{20}c} {\mu I} &{} \\ &{} {\mu I} \\ \end{array}} \right) ,V_0 = \left( {\begin{array}{*{20}c} {\mu I} &{} O \\ \end{array}} \right) ,\\ F & = {} \left( \begin{array}{l} \alpha I \\ \alpha I \\ \end{array} \right) , H_i = i\beta I,\text { for } S - s + 1 \le i \le S - 1, H_{S-s} = \left( {\begin{array}{*{20}c} O &{} {(S-s)\beta I} \\ \end{array}} \right) , \\ H_i & = {} \left( {\begin{array}{*{20}c} {i\beta I} &{}\quad {} \\ {} &{}\quad {i\beta I} \\ \end{array}} \right) ,\text { for }1 \le i \le S - s - 1,\\ G^{*} & = {} \left( \begin{array}{l} O \\ D_1^{(R)} \\ \end{array} \right) , G_i = D_0^{(R)} - (\lambda +\mu +\alpha + (S - i)\beta )I, \text { for }1 \le i \le s, \\ G_i & = {} \left( {\begin{array}{*{20}c} {G_i^0 } &{}\quad {} \\ {} &{}\quad {G_i^1 } \\ \end{array}} \right) , \text { for } s + 1 \le i \le S, G_i^0 = D^{(R)} - (\lambda +\mu +\alpha + (S - i)\beta )I,\\ G_i^1 & = {} D_0^{(R)} - (\lambda +\mu +\alpha + (S - i)\beta )I, G_{S^*} = D^{(R)} - (\lambda +\mu ) I,\\ \tilde{G}_i & = {} D_0^{(R)} - (\lambda +\alpha + (S - i)\beta )I, \text { for }1 \le i \le s, \\ \tilde{G}_i & = {} \left( {\begin{array}{*{20}c} {\tilde{G}_i^0 } &{} {} \\ {} &{} {\tilde{G}_i^1 } \\ \end{array}} \right) , \text { for } s + 1 \le i \le S, \tilde{G}_i^0 = D^{(R)} - (\lambda +\alpha + (S - i)\beta )I, \\ \tilde{G}_i^1 & = {} D_0^{(R)} - (\lambda +\alpha + (S - i)\beta )I, \tilde{G}_{S^*} = D^{(R)} - \lambda I. \end{aligned}$$
Each matrix \(A_{00}, A_0, A_1, A_2\) is a square matrix of order \(m(2S-s+2)\).