A qualitative, patient-centered perspective toward plasma products supply chain network design with risk controlling

Abstract

Motivated by a real issue in Iran blood transfusion organization and hemophilia community, this paper aims to design and plan an integrated plasma and plasma-derived medicines supply chain network to improve efficiency and timely access to high-quality services. This paper contributes to the existing literature by incorporating four factors, namely (1) quality, (2) efficiency, (3) type-differentiated demand, and (4) risk controlling into the model. To better manage the quality of plasma, we categorize fresh frozen plasma into two classes based on plasma freezing time interval. Moreover, since the number of available donors and centers accessibility affects the supply chain performance, the ideal candidate locations of plasma donation centers are evaluated through several pivotal criteria via a data envelopment analysis approach. We propose a mathematical model, based on a tactical-strategic decision in a real case. Furthermore, the robustness manages the inherent uncertainty in input data and controls the risk of probable disruption in the model, simultaneously. We consider a real case study according to hemophilia community issues in Tehran. The outcomes assist the practitioners in managing how plasma products should be manufactured to minimize the shortages and also control the robustness against uncertainty and disruption risks.

Appendices

Appendix 1

Here are the data parameters for the problem investigation under the case study of Tehran. Noteworthy, transportation costs are provided based on the distance between the facilities which are obtained by Google map.

See Tables 9, 10, 11, 12 and 13.

Table 9 An estimated quantity of SPs and RPs donation in each period

Table 10 Cost (Million Rials/unit) and capacity (in liter) parameters of each PLS collection center

Table 11 Cost of transferring FFP units from the main blood center to each hospital (Million Rials/unit)

Table 12 Cost parameters of production and inventory (Million Rials/unit)

Table 13 Capacity parameter (in liter)

Appendix 2

2.1 Notation

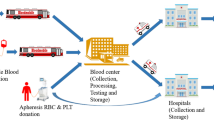
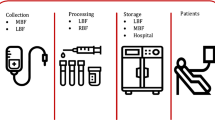
As mentioned in the study, the paper tries to solve some issues in IBTO and Hemophilia Community. Noteworthy, all these centers work under the supervision of IBTO (Cheraghali 2012), and the authors formulated and modeled the problem based on IBTO viewpoints. The notations of the proposed model are as follows:

Sets
N	Set of main blood centers, $n = 1, \ldots ,N$
h	Set of hospitals, $h = 1, \ldots , H$
$o$	Set of plasma collection centers, $o = 1, \ldots ,O$
$i$	Set of blood research and fractionation company, $i = 1, \ldots ,I$
$e$	Set of distribution centers, $e = 1, \ldots ,E$
$j$	Set of pharmacy demand points, $j = 1, \ldots ,J$
$d$	Set of FFP units age, $d = 1,..,D$
$v$	Set of types of FFP, $v = 1, \ldots ,V$
$p$	Set of PDMPs age, $p = 1, \ldots ,P$
$l$	Set of types of PDMPs, l $= 1, \ldots ,L$
$t$	Set of time periods, $t = 1, \ldots ,T$
Parameters
$C_{o}^{f}$	Establishment cost of locating plasma collection centers $o$
$CC_{h }$	Cost of inventory level of FFP units in main blood center $n$
$HC_{h }$	Cost of inventory level of FFP units in hospital $h$
$OC_{o }$	Cost of inventory level of FFP units in PLS collection center $o$
$DC_{e }$	Cost of inventory level of PDMPs in distribution center $e$
$LC_{j }$	Cost of inventory level of PDMPs in specialty pharmacy $j$
$TC^{tr}_{n,o }$	Unit cost of FFP units shipped from the main blood center $n$ to PLS collection center $o$
$MC ^{tr}_{n,h }$	Unit cost of FFP units shipped from the main blood center $n$ to hospital $h$
$BC^{tr}_{o,i }$	Unit cost of FFP units shipped from PLS collection center $o$ to BRF $i$
$KC^{tr}_{i,e }$	Unit cost of PDMPs shipped from BRF $i$ to distribution center $e$
$GC^{tr}_{e,j }$	Unit cost of PDMPs shipped from distribution center $e$ to specialty pharmacy j
$AC^{sa}_{n }$	Unit cost of the whole blood centrifuge in the main blood center $n$
$ZC^{pr}_{n }$	Unit cost of FFP units provided in the main blood center $n$
$RC^{aph}_{o }$	Unit cost of apheresis process in PLS collection center $o$
$UC^{pr}_{o }$	Unit cost of FFP units provided in PLS collection center $o$
$C^{w}_{n }$	Wastage cost of FFP units in the main blood center $n$
$CC^{w}_{h }$	Wastage cost of FFP units in hospital $h$
$EC^{w}_{e }$	Wastage cost of PDMPs in distribution center $e$
$JC^{w}_{j }$	Wastage cost of PDMPs in specialty pharmacy $j$
$SC^{sh}_{h }$	Shortage cost of FFP units in hospital $h$
$JC^{sh}_{j}$	Shortage cost of PDMPs in specialty pharmacy $j$
$wl_{n}$	Overall capacity of collecting FFP units in the main blood center $n$
$kl_{n}$	Capacity of collecting FFP units in the main blood center $n$
$ss_{o}^{'}$	Capacity of maintenance FFP units in PLS collection center $o$
$k_{i,l}$	Supply capacity of PDMPs $l$ in BRF $i$
$w_{e,l }$	Capacity of storage PDMPs $l$ in distribution center $e$
$\phi_{n}$	Maximum rate of plasma extracted from whole blood in blood center $n$
$\zeta_{\text{o}}$	Maximum rate of FFP units extracted from PLS in PLS collection center $o$.
$qa_{n,t }$	Maximum blood donation (available donor) in blood center $n$ in period $t$
$eh_{o,t }$	Maximum plasma donation in PLS collection center $o$ in period $t$
$dd_{h,d,t }$	Demand of FFP units with age $d$ in hospitals $h$ in period $t$
$db_{j,p,l,t }$	Demand of PDMPs type $l$ with age $p$ in specialty pharmacy $j$ in period t
$sf_{j,l,t}$	Safety stock level of PDMPs $l$ in specialty pharmacy $j$ in period $t$
$z_{l }$	The proportion of producing each PDMPs
$M$	A very large number
Binary variables
$\varPsi_{o }$	$1$; if the PLS collection center located in candidate location $o$; $0$ otherwise
$\beta_{n,t }$	1; if the freezers has enough capacity to freeze PLS in 2–4 h in period $t$; 0 otherwise
$\theta_{v,t }$	1; if FFP units produced with type $v$ allocated to hospital in period $t;$ 0 otherwise
$y_{j,l,t }$	1; if the specialty pharmacy is compelled to use safety stock in period $t;$ 0 otherwise
${{\Omega }}_{n,t }$	1; if PLS is extracted at the main blood center n in period t; 0 otherwise
Positive variables
$x_{n,o,v,d,t }$	Quantity of FFP units with age $d$ and type $v$ shipped from blood center $n$ to PLS collection center $o$ in period $t$
$q^{\prime\prime}_{{n,h,{\text{d}},v,t }}$	Quantity of FFP units with age $d$ and type $v$ shipped from the main blood center $n$ to hospital $h$ in period $t$
$gq_{o,i,t}$	Quantity of FFP units shipped from PLS collection center $o$ to BRF company $i$ in period $t$
$u_{i,e,l,t }$	Quantity of PDMPs $l$ shipped from BRF company $i$ to distribution center $e$ in period $t$
$v_{e,j,l,p,t }$	Quantity of PDMPs $l$ with age $p$ shipped from distribution center $e$ to specialty pharmacy $j$ in period $t$
$Nv^{ }_{n,d,v,t}$	Inventory level of FFP units with age $d$ and with type $v$ in blood center $n$ in period $t$
$Hv _{h,v,d,t}$	Inventory level of FFP units with age $d$ and type $v$ in hospital $h$ in period $t$
$Pv _{{{\text{o}},{\text{t}}}}$	Inventory level of FFP units in PLS collection center $o$ in period $t$
$Ev_{l,p,e,t}$	Inventory level of PDMPs $l$ with age $p$ in distribution center $e$ in period $t$
$Jv_{j,l,p,t }$	Inventory level of PDMPs $l$ with age $p$ in specialty pharmacy $j$ in period $t$
$hs_{h,t }$	Shortage level of FFP units in hospital $h$ in period $t$
$js_{j,l,t }$	Shortage level of PDMPs $l$ in specialty pharmacy $j$ in period $t$
$rw_{n,v,t }$	Wastage level of FFP units with type $v$ in blood center $n$ in period $t$
$hw_{h,v,t }$	Wastage level of FFP units with type $v$ in hospital $h$ in period $t$
$ew_{e,l,t }$	Wastage level of PDMPs $l$ in distribution center $e$ period $t$
$jw_{j,l,t }$	Wastage level of PDMPs $l$ in specialty pharmacy $j$ period $t$
$sq_{n,t }$	Quantity of blood donation in blood center $n$ in period $t$
$qq_{n,v,t }$	Quantity of plasma extracted from whole blood in the main blood center $n$ by considering type $v$ in period $t$
$q_{o,t }$	Quantity of plasmapheresis donation in PLS collection center o in period t
$q^{\prime}_{o,t }$	Quantity of FFP units in PLS collection center $o$ in period t

2.2 Robust optimization

In this study, based on different types of patients in hospitals as moderate and severe type, and specialty pharmacies (patients require Albumin, IVIG, or Factor VIII), two types of demand including FFP units and PDMPs $(\widetilde{dd}_{h,\varphi ,t } , \widetilde{db}_{j,p,l,t } )$ are considered as unknown parameters. Note that the transportation cost parameters ($\widetilde{MC}_{n,h }$, $\widetilde{TC}_{n,o }$, $\widetilde{BC}_{o,i }$, $\widetilde{KC}_{i,e }$ and $\widetilde{XC}_{e,j }$) are considered uncertain due to traffic risks. Moreover, $\eta_{n,h}^{n} , \eta_{n,o}^{ 'n} , \eta_{o,i}^{o} , \eta_{i,e}^{i} , \eta_{e,j}^{e}$ reflect described variables corresponding to the constraints of the robust-box linear optimization. The investigated deterministic model is extended to the robust optimization model as follows:

$$\hbox{min} \;w$$

(33)

Subject to:

$$\begin{aligned} & \mathop \sum \limits_{n,h,v,d,t} (\overline{MC}_{n,h}^{tr} \times q_{n,h,d,v,t}^{{\prime \prime }} + \eta_{n,h}^{n} ) + \mathop \sum \limits_{n,o,v,d,t} (\overline{TC}_{n,o}^{tr} \times x_{n,o,v,d,t } + \eta_{n,o}^{{{\prime }n}} ) \\ & \quad + \mathop \sum \limits_{o,i,t} (\overline{BC}_{o,i}^{tr} \times gq_{o,i,t} + \eta_{o,i}^{o} ) + \mathop \sum \limits_{i,e,l,p,t} (\overline{KC}_{i,e}^{tr} \times u_{i,e,l,t } + \eta_{i,e}^{i} ) \\ & \quad + \mathop \sum \limits_{e,j,l,p,t} \left( {\overline{GC}_{e,j}^{tr} \times v_{e,j,l,p,t } + \eta_{e,j}^{e} } \right) + \mathop \sum \limits_{o} C_{o}^{f} *\varPsi_{o } + \mathop \sum \limits_{n,v,d,t} CC_{n } \times Nv^{ }_{n,d,v,t} \\ & \quad + \mathop \sum \limits_{h,d,t} HC_{h } \times Hv _{h,v,d,t} + \mathop \sum \limits_{o,t} OC_{o } \times Pv _{o,t} + \mathop \sum \limits_{l,e,p,t} DC_{e } \times Ev_{l,p,e,t} \\ & \quad + \mathop \sum \limits_{n,t} AC^{sa}_{n } \times sq_{n,t } + \mathop \sum \limits_{n,t} \mu_{n,t } \times ZC^{pr}_{n } + \mathop \sum \limits_{o,t} RC^{aph}_{o } \times q_{o,t } \\ & \quad + \mathop \sum \limits_{o,t} UC^{pr}_{o } \times q_{o,t}^{{\prime }} + \mathop \sum \limits_{h,t} hs_{h,t } \times SC^{sh}_{h } + \mathop \sum \limits_{j,l,t} js_{j,l,t } \times JC^{sh}_{j} \\ & \quad + \mathop \sum \limits_{n,v,t} rw_{n,v,t } \times C^{w}_{n } + \mathop \sum \limits_{h,v,t} hw_{h,v,t } \times CC^{w}_{h } + \mathop \sum \limits_{e,l,t} ew_{e,l,t } \times EC^{w}_{e } \\ & \quad + \mathop \sum \limits_{j,l,t} jw_{j,l,t } \times JC^{w}_{j } \le w \\ \end{aligned}$$

(34)

$$\rho \times MC ^{tr}_{n,h } \times q_{n,h,d,v,t}^{{\prime \prime }} \le \eta_{n,h}^{n} \quad \forall \;n,h,v,t,d$$

(35)

$$\rho \times MC ^{tr}_{n,h } \times q_{n,h,d,v,t}^{{\prime \prime }} \ge - \eta_{n,h}^{n} \quad \forall \;n,h,v,t,d$$

(36)

$$\rho \times TC^{tr}_{n,o } \times x_{n,o,v,d,t } \le \eta_{n,o}^{{{\prime }n}} \quad \forall \;n,o,v,t,d$$

(37)

$$\rho \times TC^{tr}_{n,o } \times x_{n,o,v,d,t } \ge - \eta_{n,o}^{{{\prime }n}} \quad \forall \;n,o,v,t,d$$

(38)

$$\rho \times BC^{tr}_{o,i } \times gq_{o,i,t} \le \eta_{o,i}^{o} \quad \forall \;o,i,t$$

(39)

$$\rho \times BC^{tr}_{o,i } \times gq_{o,i,t} \ge - \eta_{o,i}^{o} \quad \forall \;o,i,t$$

(40)

$$\rho \times KC^{tr}_{i,e } \times u_{i,e,l,t } \le \eta_{i,e}^{i} \quad \forall \;i,e,l,t$$

(41)

$$\rho \times KC^{tr}_{i,e } \times u_{i,e,l,t } \ge - \eta_{i,e}^{i} \quad \forall \;i,e,l,t$$

(42)

$$\rho \times GC^{tr}_{e,j } \times v_{e,j,l,p,t } \le \eta_{e,j}^{e} \quad \forall \;e,j,l,p,t$$

(43)

$$\rho \times GC^{tr}_{e,j } \times v_{e,j,l,p,t } \ge - \eta_{e,j}^{e} \quad \forall \;e,j,l,p,t$$

(44)

$$\mathop \sum \limits_{v,d} Hv _{{{\text{h}},v,d,t}} = \mathop \sum \limits_{v,d} Hv _{{{\text{h}},v,d - 1,t - 1}} + \mathop \sum \limits_{n,v,d} q_{n,h,d,v,t}^{{\prime \prime }} - \mathop \sum \limits_{d} {\text{dd}}_{{{\text{h}},d,t }} - \left( {\rho_{1} \times \mathop \sum \limits_{\text{d}} dd_{{{\text{h}},{\text{d}},{\text{t }}}} } \right) + hs_{h,t } \quad \forall \;h,t \ge 2$$

(45)

$$\mathop \sum \limits_{p} Jv_{j,l,p,t } = \mathop \sum \limits_{p} Jv_{j,l,p - 1,t - 1 } + \mathop \sum \limits_{e,p} v_{e,j,l,p,t } - \mathop \sum \limits_{p} db_{j,p,l,t } - \left( {\rho_{2} \times \mathop \sum \limits_{p} db_{j,p,l,t } } \right) + js_{j,l,t } \quad \forall \;j,l,t \ge 2$$

(46)

and constraints (3)–(11), (13)–(26), (28)–(31).

The objective function (1) is converted to (33), and constraints (34)–(46) are added based on the Box-uncertainty approach.

2.3 Reliable model

$$\begin{aligned} & \mathop \sum \limits_{o} C_{o}^{f} \times \varPsi_{o } + \mathop \sum \limits_{n,v,d,t} CC_{n } \times Nv_{n,d,v,t}^{0} + \mathop \sum \limits_{h,d,t} HC_{h } \times Hv_{{{\text{h}},v,d,t}}^{0} + \mathop \sum \limits_{o,t} OC_{o } \times Pv_{{{\text{o}},{\text{t}}}}^{0} \\ & \quad + \mathop \sum \limits_{l,e,p,t} DC_{e } \times Ev^{0}_{l,p,e,t} + \mathop \sum \limits_{j,l,p,t} Jv_{j,l,p,t}^{0} \times LC_{j } + \mathop \sum \limits_{n,h,v,d,t} (MC ^{tr}_{n,h } \times q_{n,h,d,v,t}^{{{\prime \prime }0}} + {{\upeta }}_{n,h}^{n0} ) \\ & \quad + \mathop \sum \limits_{n,o,v,d,t} (TC^{tr}_{n,o } \times x_{n,o,v,d,t}^{0} + {{\upeta }}_{n,o}^{n0} ) + \mathop \sum \limits_{o,i,t} (BC^{tr}_{o,i } \times gq_{o,i,t}^{0} + {{\upeta }}_{o,i}^{o0} ) \\ & \quad + \mathop \sum \limits_{i,e,l,p,t} (KC^{tr}_{i,e } \times u_{i,e,l,t}^{0} + {{\upeta }}_{i,e}^{i0} ) + \mathop \sum \limits_{e,j,l,p,t} GC^{tr}_{e,j } \times v_{e,j,l,p,t}^{0} + {{\upeta }}_{e,j}^{e0} ) \\ & \quad + \mathop \sum \limits_{n,t} A{\text{C}}^{sa}_{\text{n }} \times {\text{sq}}_{{{\text{n}},{\text{t }}}}^{0} + \mathop \sum \limits_{n,t} {{\Omega }}_{n,t}^{0} \times ZC^{pr}_{n } + \mathop \sum \limits_{o,t} RC^{aph}_{o } \times {\text{q}}_{{{\text{o}},{\text{t }}}}^{0} \\ & \quad + \mathop \sum \limits_{o,t} UC^{pr}_{o } \times q^{{{\prime }0}}_{o,t } + \mathop \sum \limits_{h,t} hs_{h,t}^{0} \times SC^{sh}_{h } + \mathop \sum \limits_{j,l,t} js_{j,l,t}^{0} \times JC^{sh} + \mathop \sum \limits_{n,v,t} rw_{n,v,t}^{0} \times C^{w}_{n } \\ & \quad + \mathop \sum \limits_{h,v,t} hw_{h,v,t}^{0} \times CC^{w}_{h } + \mathop \sum \limits_{e,l,t} ew_{e,l,t}^{0} \times EC^{w}_{e } + \mathop \sum \limits_{j,l,t} JC^{w}_{j } \times jw_{j,l,t}^{0} \\ \end{aligned}$$

(47)

Subject to:

$$\begin{aligned} &\mathop \sum \limits_{o} C_{o}^{f} \times \varPsi_{o } + \mathop \sum \limits_{n,h,v,d,t} (MC ^{tr}_{n,h } \times q_{n,h,\varphi ,v,t}^{{ \prime\prime {\text{s}}}} + {{\upeta }}_{n,h}^{ns} ) + \mathop \sum \limits_{n,o,v,d,t} (TC^{tr}_{n,o } \times x_{n,o,v,d,t}^{s} + {{\upeta }}_{n,o}^{ns} ) \hfill \\& + \mathop \sum \limits_{o,i,t} (BC^{tr}_{o,i } *gq_{o,i,t}^{s} + {{\upeta }}_{o,i}^{os} ) + \mathop \sum \limits_{i,e,l,p,t} (KC^{tr}_{i,e } \times u_{i,e,l,t}^{s} + {{\upeta }}_{i,e}^{is} ) \hfill \\& + \mathop \sum \limits_{e,j,l,p,t} (GC^{tr}_{e,j } \times v_{e,j,l,p,t}^{s} + {{\upeta }}_{e,j}^{es} ) + \mathop \sum \limits_{n,t} A{\text{C}}^{sa}_{\text{n }} \times {\text{sq}}_{{{\text{n}},{\text{t }}}}^{s} \hfill \\& { + }\mathop \sum \limits_{n,t} {{\Omega }}_{n,t}^{s} \times ZC^{pr}_{n } + \mathop \sum \limits_{o,t} RC^{aph}_{o } \times {\text{q}}_{{{\text{o}},{\text{t }}}}^{s} + \mathop \sum \limits_{o,t} UC^{pr}_{o } \times q^{{ \prime {\text{s}}}}_{o,t } \hfill \\& + \mathop \sum \limits_{h,t} hs_{h,t}^{s} \times SC^{sh}_{h } + \mathop \sum \limits_{j,l,t} js_{j,l,t}^{s} \times JC^{sh} + \mathop \sum \limits_{n,v,t} rw_{n,v,t}^{s} \times C^{w}_{n } + \mathop \sum \limits_{h,v,t} hw_{h,v,t}^{s} \times CC^{w}_{h } \hfill \\& + \mathop \sum \limits_{e,l,t} ew_{e,l,t}^{s} \times EC^{w}_{e } + \mathop \sum \limits_{j,l,t} JC^{w}_{j } \times jw_{j,l,t}^{s} \le K_{s}^{*} \times \left( {1 + p} \right), \forall s \in S/\left\{ 0 \right\}. \hfill \\ \end{aligned}$$

(48)

$${\text{sq}}_{{{\text{n}},{\text{t }}}}^{s} \le {\text{qa}}_{{{\text{n}},{\text{t }}}} \quad \forall \;n,t,s$$

(49)

$$\mathop \sum \limits_{v} qq_{n,v,t}^{s} = \phi_{n} \times {\text{sq}}_{{{\text{n}},{\text{t }}}}^{s} \quad \forall \;n,t,s$$

(50)

$$\mathop \sum \limits_{v} qq_{n,v,t}^{s} \le wl_{n} \times {{\Omega }}_{n,t}^{s} \quad \forall \;n,t,s$$

(51)

$$qq_{n,v,t}^{s} \le kl_{n} \quad \forall \;n,t,v = 1,s$$

(52)

$$\beta_{n,t}^{s} \le 1 - \left( {\frac{{kl_{n} - qq_{n,v,t}^{s} }}{{kl_{n} }}} \right) \quad \forall \;n,t,v = 1,s$$

(53)

$$qq_{n,v,t}^{s} \le \beta_{n,t}^{s} \times M \quad \forall \;n,t,v = 2,s$$

(54)

$$Nnv_{n,d,v,t}^{s} = qq_{n,v,t}^{s} - \mathop \sum \limits_{h} q_{n,h,d,v,t}^{{ \prime\prime {\text{s}}}} - \mathop \sum \limits_{o} x_{n,o,v,d,t}^{s} \quad \forall \;n,v,d = 1,t \ge 2,s$$

(55)

$$\mathop \sum \limits_{d > 1} Nv_{n,d,v,t}^{s} = \mathop \sum \limits_{d > 1} Nv_{n,d - 1,v,t - 1}^{s} - \mathop \sum \limits_{h,d > 1} q_{n,h,d,v,t}^{{ \prime\prime {\text{s}}}} - \mathop \sum \limits_{o,d > 1} x_{n,o,v,d,t}^{s} \quad \forall \;n,v,t \ge 2,s$$

(56)

$$rw_{n,v,t}^{s} = Nv_{n,d,v,t}^{s} \quad \forall \;n,v,d = 12,t,s$$

(57)

$$\mathop \sum \limits_{v,d} Hv_{{{\text{h}},v,d,t}}^{s} = \mathop \sum \limits_{v,d} Hv_{{{\text{h}},v,d - 1,t - 1}}^{s} + \mathop \sum \limits_{n,v,d} q_{n,h,d,v,t}^{{ \prime\prime {\text{s}}}} - \mathop \sum \limits_{d} {\text{dd}}_{{{\text{h}},d,t }} - (\rho_{1} \times\mathop \sum \limits_{d} {\text{dd}}_{{{\text{h}},d,t }} ) + hs_{h,t}^{s} \quad \forall \;h,t \ge 2,{\text{s}}$$

(58)

$$\theta_{v - 1,t}^{s} \ge \theta_{v,t}^{s} \quad \forall \;t,v \ge 2,s$$

(59)

$$q_{n,h,d,v,t}^{{ \prime\prime {\text{s}}}} \le \theta_{v,t}^{s} \times M \quad \forall \;n,h,v,d,t,s$$

(60)

$$Hv_{{{\text{h}},v,d,t}}^{s} \le M \times \left( {1 - \theta_{v,t}^{s} } \right) \quad \forall \;h,v,d,t,s$$

(61)

$$hw_{h,v,t}^{s} = Hv_{{{\text{h}},v,d,t}}^{s} \quad \forall \;h,v,t,s,d = 12$$

(62)

$${\text{q}}_{{{\text{o}},{\text{t }}}}^{s} \le {\text{eh}}_{{{\text{o}},{\text{t }}}} \quad \forall \;o,t,s$$

(63)

$${\text{q}}_{{{\text{o}},{\text{t }}}}^{s} \le M \left( {1 - \pi_{o}^{s} } \right){{\Psi }}_{\text{o }} \quad \forall \;o,t,s$$

(64)

$${\text{q}}_{{{\text{o}},{\text{t }}}}^{s} \times \zeta_{\text{o}} = {\text{q}}_{{{\text{o}},{\text{t}}}}^{{{\prime }s}} \quad \forall \;o,t,s$$

(65)

$$\mathop \sum \limits_{n,v,d} x_{n,o,v,d,t}^{s} + {\text{q}}_{{{\text{o}},{\text{t}}}}^{{{\prime }s}} \le \left( {1 - \pi_{o}^{s} } \right) \times ss_{o}^{{\prime }} \times {{\Psi }}_{\text{o }} \quad \forall \;o,t,s$$

(66)

$$Pv_{{{\text{o}},{\text{t}}}}^{s} = Pv_{{{\text{o}},{\text{t}} - 1}}^{s} - \mathop \sum \limits_{i} gq_{o,i,t}^{s} + \mathop \sum \limits_{n,v,d} x_{n,o,v,d,t}^{s} + {\text{q}}_{{{\text{o}},{\text{t}}}}^{{{\prime }s}} \quad \forall \;o,t \ge 2,s$$

(67)

$$\mathop \sum \limits_{e} u_{i,e,l,t}^{s} \le {\text{k}}_{{{\text{i}},{\text{l}}}} \quad \forall \;i,l,t, s$$

(68)

$$\mathop \sum \limits_{i} gq_{o,i,t}^{s} \times z_{l } \ge \mathop \sum \limits_{e} u_{i,e,l,t}^{s} \quad \forall i,l,t,s$$

(69)

$$\mathop \sum \limits_{p,j} v_{e,j,l,p,t}^{s} \le w_{e,l } \quad \forall \;e,l,t,s$$

(70)

$$Ev^{\text{s}}_{l,p,e,t} = \mathop \sum \limits_{i} u_{i,e,l,t}^{s} - \mathop \sum \limits_{j} v_{e,j,l,p,t}^{s} \quad \forall \;e,l,p = 1,t \ge 2,s$$

(71)

$$Ev^{\text{s}}_{l,p,e,t} = Ev^{\text{s}}_{l,p - 1,e,t - 1} - \mathop \sum \limits_{j} v_{e,j,l,p,t}^{s} \quad \forall \;e,l,p \ge 2,t \ge 2,s$$

(72)

$$ew_{e,l,t}^{s} = Ev^{\text{s}}_{l,p,e,t} \quad \forall \;e,l,t,p = 12,s$$

(73)

$$\mathop \sum \limits_{p} Jv_{j,l,p,t}^{s} = \mathop \sum \limits_{p} Jv_{j,l,p - 1,t - 1}^{s} + \mathop \sum \limits_{e,p} v_{e,j,l,p,t}^{s} - \mathop \sum \limits_{p} db_{j,p,l,t } - (\rho_{2} \mathop \sum \limits_{p} db_{j,p,l,t } ) + js_{j,l,t}^{s} \quad \forall \;j,l,t \ge 2$$

(74)

$$jw_{j,l,t}^{s} = Jv_{j,l,p,t}^{s} \quad \forall \;j,l,t,p = 12,s$$

(75)

$$\mathop \sum \limits_{p < 12} Jv_{j,l,p,t}^{s} \ge \left( {1 - y_{j,l,t}^{s} } \right) \times sf_{j,l,t} \quad \forall \;j,l,t,s$$

(76)

$$y_{j,l,t}^{s} \le M \times js_{j,l,t}^{s} \quad \forall \;j,l,t \ge 2,s$$

(77)

$$\rho *MC^{tr}_{n,h } \times q^{{ \prime\prime {\text{s}}}}_{n,h,d,v,t } \le {{\upeta }}_{n,h}^{ns} \quad \forall \;n,h,v,t,d,s$$

(78)

$$\rho *MC^{tr}_{n,h } \times q^{{ \prime\prime {\text{s}}}}_{n,h,d,v,t } \ge - {{\upeta }}_{n,h}^{ns} \quad \forall \;n,h,v,t,d,s$$

(79)

$$\rho \times TC^{tr}_{n,o } \times x_{n,o,v,d,t}^{s} \le {{\upeta }}_{n,o}^{ns} \quad \forall \;n,o,v,t,d,s$$

(80)

$$\rho \times TC^{tr}_{n,o } \times x_{n,o,v,d,t}^{s} \ge - {{\upeta }}_{n,o}^{ns} \quad \forall \;n,o,v,t,d,s$$

(81)

$$\rho \times BC^{tr}_{o,i } \times gq_{o,i,t}^{s} \le {{\upeta }}_{o,i}^{os} \quad \forall \;o,i,t,s$$

(82)

$$\rho \times BC^{tr}_{o,i } \times gq_{o,i,t}^{s} \ge -{{ \upeta }}_{o,i}^{os} \quad \forall \;o,i,t,s$$

(83)

$$\rho \times KC^{tr}_{i,e } \times u_{i,e,l,t}^{s} \le {{\upeta }}_{i,e}^{is} \quad \forall \;i,e,l,t,s$$

(84)

$$\rho \times KC^{tr}_{i,e } \times u_{i,e,l,t}^{s} \ge - {{\upeta }}_{i,e}^{is} \quad \forall \;i,e,l,t,s$$

(85)

$$\rho \times GC^{tr}_{e,j } \times v_{e,j,l,p,t}^{s} \le {{\upeta }}_{e,j}^{es} \quad \forall e,j,l,p,t,s$$

(86)

$$\rho \times GC^{tr}_{e,j } \times v_{e,j,l,p,t}^{s} \ge - {{\upeta }}_{e,j}^{es} \quad \forall e,j,l,p,t,s$$

(87)

$$\begin{aligned} {\text{sq}}_{{{\text{n}},{\text{t }}}}^{s} ,qq_{n,v,t}^{s} , q_{n,h,d,v,t}^{{ \prime\prime {\text{s}}}} , x_{n,o,v,d,t}^{s} , Nv_{n,d,v,t}^{s} , rw_{n,v,t}^{s} , Hv_{{{\text{h}},v,d,t}}^{s} ,Pv_{{{\text{o}},{\text{t}}}}^{s} ,hs_{h,t}^{s} , hw_{h,v,t}^{s} ,{\text{q}}_{{{\text{o}},{\text{t }}}}^{s} , {\text{q}}_{{{\text{o}},{\text{t}}}}^{'s} , gq_{o,i,t}^{s} ,u_{i,e,l,t}^{s} , v_{e,j,l,p,t}^{s} , Ev^{\text{s}}_{l,p,e,t} , ew_{e,v,t}^{s} ,Jv_{j,l,p,t}^{s} ,js_{j,l,t}^{s} \ge 0\;\forall \;j,l,t,n,v,p,d,o ,e, h, s \end{aligned}$$

(88)

$$\mu_{n,t}^{s} ,\beta_{n,t}^{s} ,\theta_{v,t}^{s} ,y_{j,l,t}^{s} ,{{\Psi }}_{\text{o }} \in \left\{ {0,1} \right\}$$

(89)