Abstract
In the case of the proportional output reduction strategy with a single output, the Variable-Returns-to-Scale (VRS) Zero-Sum Gains Data Envelopment Analysis (ZSG-DEA) efficiency scores can be obtained from the VRS conventional DEA efficiency scores by means of the Target’s Assessment Theorem (TAT). Using TAT as a departure point, two relations for computing the ZSG-DEA efficiency scores appear in the literature. Our objective in this note is to compare, contrast and challenge them on both theoretical and empirical grounds. For the latter, three different data sets are used.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
Lins et al. (2003) estimated the ZSG-DEA efficiency scores of countries in the Olympic Games by using as a single output the a priori fixed number of their total (gold, silver and bronze) medals won.
Gomes and Lins (2008) coined the names TAT and BCET since these are respectively referred to as Theorem and Corollary in Lins et al. (2003).
For this reason, Bi et al. (2014) wrote the ZSG-DEA model by excluding the DMU under evaluation from the reference set.
If \({\widehat{h}}^{k}>{1}\), then \({\lambda }_{k}^{k}={0}\) and thus (3) is the same as the model in Bi et al.’s (2014) Eq. (3).
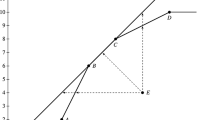
The left-hand side term in (4) is equal to \({x}^{k}c{^{\prime}}\) in Fig. 1, the first right-hand side term in (4) is equal to \({x}^{k}c\), and thus \({RC}^{k}=\frac{{x}^{k}c{^{\prime}}}{{x}^{k}c}\) corresponds to the vertical distance between TDEA and TZSG-DEA at \({x}^{k}\).
In terms of Fig. 1, this means that DMUs \(a\) and \(b\) are on both the conventional DEA and the ZSG-DEA frontiers while DMU \(k\) is inefficient with respect to both frontiers.
References
Andersen P, Petersen NC (1993) A procedure for ranking efficient units in data envelopment analysis. Manag. Sci. 39:1261–1264
Bi G, Feng C, Ding J, Liang L, Chu F (2014) The linear formulation of the ZSG-DEA models with different production technologies. J. Oper. Res. Soc. 65:1202–1211
Churilov L, Flitman A (2006) Towards fair ranking of Olympics achievements: the case of Sydney 2000. Comput. Oper. Res. 33:2057–2082
Collier T, Johnson AL, Ruggiero J (2011) Measuring technical efficiency in sports. J. Sports Econ. 12:579–598
Gomes EG, Lins MPE (2008) Modelling undesirable outputs with zero sum gains data envelopment analysis models. J. Oper. Res. Soc. 59:616–623
Hu J-L, Fang C-Y (2010) Do market share and efficiency matter for each other? An application of the zero-sum gains data envelopment analysis. J. Oper. Res. Soc. 61:647–657
Lins MPE, Gomes EG, Soares de Mello JCCB, Soares de Mello AJR (2003) Olympic ranking based on a zero sum gains DEA model. Eur. J. Oper. Res. 148:312–322
Yang F, Wu DD, Liang L, O’Neill L (2011) Competition strategy and efficiency evaluation for decision making units with fixed-sum outputs. Eur. J. Oper. Res. 212:560–569
Acknowledgments
The first author acknowledges the financial support of the State Scholarships Foundation of Greece (IKY). We want to thank three anonymous referees for the useful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Bouzidis, T., Karagiannis, G. A note on the zero-sum gains data envelopment analysis model. Oper Res Int J 22, 1737–1758 (2022). https://doi.org/10.1007/s12351-021-00631-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12351-021-00631-8