Abstract
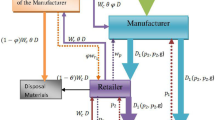
This study investigates reverse channel choice for a bi-level closed-loop supply chain consisting of a manufacturer and a retailer. In the forward channel, the manufacturer sells the products through the retailer. We consider three collection channels to collect end-of-use products for the reverse channel: (1) retailer collection (R model), (2) manufacturer and retailer hybrid collection (MRH model), and (3) manufacturer and retailer competitive collection (MRC model). This study considers both manufacturer leadership and retailer leadership for all these three models. After obtaining the members' optimal decisions in the different models using backward induction, the models were applied to a vacuum cleaner company's data in Iran. A comparison of these models shows that the retailer leadership was better than the manufacturer leadership. From the manufacturer leadership perspective, the MRH model is the best one. From the retailer leadership perspective, the prices, the retailer collection rate, and the retail profit are the same in the R and MRH models, while the total collection rate and the total yield are more extensive in the MRH model than in the R model. The MRH model is better than the MRC model at any competition intensity. Moreover, this study indicates that the range of competition intensity between two collection channels in which the MRC model outperforms the R model is different under the retailer leadership and the manufacturer leadership. The results of this study can be used as a reference for reverse channel selection. Finally, we perform a sensitivity analysis for the model parameters.







Similar content being viewed by others
References
Alamdar S, Rabbani M, Heydari J (2019) Optimal decision problem in a three-level closed-loop supply chain with risk-averse players under demand uncertainty. Uncertain Supply Chain Manag 7(2):351–368
Choi TM, Li Y, Xu L (2013) Channel leadership, performance and coordination in closed loop supply chains. Int J Prod Econ 146(1):371–380
European Remanufacturing Network, 2015. Remanufacturing market study (645984). Accessed: 15th Feb. 2015. http://www.remanufacturing.eu/europeanremanufacturingindustry-esimated-at-e30bn-with-potential-to-triple-by-2030/
Gao J, Han H, Hou L, Wang H (2016) Pricing and effort decisions in a closed-loop supply chain under different channel power structures. J Clean Prod 112:2043–2057
Giri BC, Chakraborty A, Maiti T (2017) Pricing and return product collection decisions in a closed-loop supply chain with dual-channel in both forward and reverse logistics. J Manuf Syst 42:104–123
Hong X, Wang Z, Wang D, Zhang H (2013) Decision models of closed-loop supply chain with remanufacturing under hybrid dual-channel collection. Int J Adv Manuf Technol 68(5–8):1851–1865
Hong X, Xu L, Du P, Wang W (2015) Joint advertising, pricing and collection decisions in a closed-loop supply chain. Int J Prod Econ 167:12–22
Hong X, Zhang H, Zhong Q, Liu L (2016) Optimal decisions of a hybrid manufacturing-remanufacturing system within a closed-loop supply chain. Eur J Ind Eng 10(1):21–50
Huang Y, Wang Z (2017) Dual-recycling channel decision in a closed-loop supply chain with cost disruptions. Sustainability 9(11):2004
Huang M, Song M, Lee LH, Ching WK (2013) Analysis for strategy of closed-loop supply chain with dual recycling channel. Int J Prod Econ 144(2):510–520
Jensen JP, Prendeville SM, Bocken NM, Peck D (2019) Creating sustainable value through remanufacturing: Three industry cases. J Clean Prod 218:304–314
Jung KS, Hwang H (2011) Competition and cooperation in a remanufacturing system with take-back requirement. J Intell Manuf 22(3):427–433
Liu L, Wang Z, Xu L, Hong X, Govindan K (2017) Collection effort and reverse channel choices in a closed-loop supply chain. J Clean Prod 144:492–500
Maiti T, Giri BC (2015) A closed loop supply chain under retail price and product quality dependent demand. J Manuf Syst 37:624–637
Modak NM, Modak N, Panda S, Sana SS (2018) Analyzing structure of two-echelon closed-loop supply chain for pricing, quality and recycling management. J Clean Prod 171:512–528
Moslehi MS, Sahebi H, Teymouri A (2020) A multi-objective stochastic model for a reverse logistics supply chain design with environmental considerations. J Ambient Intell Hum Comput 1–24. https://doi.org/10.1007/s12652-020-02538-2
Ranjbar Y, Sahebi H, Ashayeri J, Teymouri A (2020) A competitive dual recycling channel in a three-level closed loop supply chain under different power structures: pricing and collecting decisions. J Clean Prod 272:122623
Sadjadi SJ, Asadi H, Sadeghian R, Sahebi H (2018) Retailer Stackelberg game in a supply chain with pricing and service decisions and simple price discount contract. PLoS ONE 13(4):e0195109
Sahebi H, Nickel S, Ashayeri J (2014) Environmentally conscious design of upstream crude oil supply chain. Ind Eng Chem Res 53(28):11501–11511
Sahebi H, Nickel S, Ashayeri J (2015) Joint venture formation and partner selection in upstream crude oil section: goal programming application. Int J Prod Res 53(10):3047–3061
Savaskan RC, Van Wassenhove LN (2006) Reverse channel design: the case of competing retailers. Manage Sci 52(1):1–14
Savaskan RC, Bhattacharya S, Van Wassenhove LN (2004) Closed-loop supply chain models with product remanufacturing. Manage Sci 50(2):239–252
SeyedEsfahani MM, Biazaran M, Gharakhani M (2011) A game theoretic approach to coordinate pricing and vertical co-op advertising in manufacturer–retailer supply chains. Eur J Oper Res 211(2):263–273
Shi Y, Nie J, Qu T, Chu LK, Sculli D (2015) Choosing reverse channels under collection responsibility sharing in a closed-loop supply chain with remanufacturing. J Intell Manuf 26(2):387–402
Taleizadeh AA, Moshtagh MS, Moon I (2017) Optimal decisions of price, quality, effort level and return policy in a three-level closed-loop supply chain based on different game theory approaches. Eur J Ind Eng 11(4):486–525
Tao F, Fan T, Jia X, Lai KK (2019). Optimal production strategy for a manufacturing and remanufacturing system with return policy. Oper Res 21:1–21.
U.S. International Trade Commission, 2012. Remanufactured goods: an overview of the U.S. And global industries, markets, and trade .https://www.usitc.gov/publications/332/pub4356.pdf. (Accessed 8 November 2016).
Wang W, Zhang Y, Zhang K, Bai T, Shang J (2015) Reward–penalty mechanism for closed-loop supply chains under responsibility-sharing and different power structures. Int J Prod Econ 170:178–190
Wang N, He Q, Jiang B (2018) Hybrid closed-loop supply chains with competition in recycling and product markets. Int J Prod Econ 217:246–258
Wei J, Govindan K, Li Y, Zhao J (2015) Pricing and collecting decisions in a closed-loop supply chain with symmetric and asymmetric information. Comput Oper Res 54:257–265
Wei J, Wang Y, Zhao J, Gonzalez ED (2019) Analyzing the performance of a two-period remanufacturing supply chain with dual collecting channels. Comput Ind Eng 1(135):1188–1202
Wu X, Zhou Y (2017) The optimal reverse channel choice under supply chain competition. Eur J Oper Res 259(1):63–66
Wu X, Zhou Y (2019) Buyer-specific versus uniform pricing in a closed-loop supply chain with third-party remanufacturing. Eur J Oper Res 273(2):548–560
Xu J, Liu N (2017) Research on closed loop supply chain with reference price effect. J Intell Manuf 28(1):51–64
Yao WX, Chen MM (2007) Comparison among closed-loop supply chain models. Commer Res 1:51–53
Zerang ES, Taleizadeh AA, Razmi J (2018) Analytical comparisons in a three-echelon closed-loop supply chain with price and marketing effort-dependent demand: game theory approaches. Environ Dev Sustain 20(1):451–478
Zhang Z, Liu S, Niu B (2020) Coordination mechanism of dual-channel closed-loop supply chains considering product quality and return. J Clean Prod 248:119273
Zheng B, Yang C, Yang J, Zhang M (2017) Dual-channel closed loop supply chains: Forward channel competition, power structures and coordination. Int J Prod Res 55(12):3510–3527
Zheng Y, Shu T, Wang S, Chen S, Lai KK, Gan L (2018) Analysis of product return rate and price competition in two supply chains. Oper Res Int J 18(2):469–496
Zied H, Sofiene D, Nidhal R (2014) Joint optimisation of maintenance and production policies with subcontracting and product returns. J Intell Manuf 25(3):589–602
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
Appendix A
R-M Model, retailer collection-manufacturer Stackelberg
-
Problem of retailer
To investigate the concavity of retailer profit function, its Hessian matrix has to be formed as,
For the retailer profit function to be concave, the determinants of the above Hessian matrix are required to be negative and positive decussate—i.e. \(\left| {H_{1} } \right| < 0, \, \left| {H_{2} } \right| > 0\)- in which case, if \(4C_{L} > \beta (b - A)^{2}\), the retailer profit function is concave compared to \(p^{R - M} , \, \tau_{R}^{R - M}\) and it has a unique optimal solution as,
-
Problem of manufacturer
replacing (A-4) and (A-5) in the manufacturer profit function and considering \(Y = 4C_{L} - \beta (b - A)^{2}\) and \(S = (b - A)(\Delta - b)\), we will have,
To investigate the concavity of the manufacturer profit function, the second derivative of the above equation should be calculated due to the wholesale price \(W^{R - M}\) as,
Considering \(\frac{{\partial^{2} \hat{\Pi }_{M}^{R - M} }}{{\partial (W^{R - M} )^{2} }} < 0\), the manufacturer profit function is concave. Now, the wholesale price is obtained as,
Replacing (9) in the manufacturer profit function gives
Since the above equation is always incremental to b, b equals to its upper limit and we have,
Now the wholesale price is obtained as
Replacing \(W^{R - M*}\) in \(\hat{p}^{R - M} , \, \hat{\tau }_{R}^{R - M}\) equations gives the optimal wholesale prices and retailer collection rate as,
Limitation \(0 \le \tau_{R}^{R - M*} < 1\) completes this section.
R-R Model, retailer collection-retailer Stackelberg
-
Problem of manufacturer
Since the manufacturer’s profit increases as W increases and given limitation \(w < p\), let us assume the manufacturer’s profit to be the average of the retailer’s profit margin and wholesale price as,
The above inference is similar to the approach assumption employed in Taleizadeh et al. (2017), Maiti and Giri (2015), Giri et al. (2017), and SeyedEsfahani et al. (2011) to solve the retailer Stackelberg model.
-
Problem of retailer
replacing \(\hat{W}^{R - R}\) in the retailer profit function gives,
Let us investigate the concavity of the retailer profit function as,
For the retailer profit function to be concave, its Hessian matrix is required to be negative definite. Thus, the retailer profit function will be concave with a unique optimal solution if the following condition is satisfied,
Now, the retailer’s best reactions will be as follows using the first-order condition,
Replacing \(\hat{p}^{R - R}\) in \(\hat{W}^{R - R}\) equation gives the wholesale price as,
Now, the following equation is obtained by replacing (A-24) in the manufacturer profit function as,
According to Savaskan et al. (2004) and Hong et al. (2013), the manufacturer transfers the entire saving resulted from remanufacturing to the retailer because of the retailer’s collection rate increases as b increases, resulting in the reduced manufacturing cost \(\overline{C} = C_{m} - \Delta \tau\). Also, an increase in the transfer price makes the retailer reduce the retail price. Thus, the increased demand and reduced manufacturing cost increases the profit, and thus \(b = \Delta\).
The lower the transfer price (b) is than the net saved costs resulted from remanufacturing (\(\Delta\)) compared to when \(b = \Delta\), the prices decline and the collection rate rises lower due to the double marginalization and thus the profit rises lower. Of course, it can be observed in equations \(\hat{\rm p}^{{\rm R - R}} ,\,\hat{\uptau }_{\rm R}^{{{\rm R} - {\rm R}}} ,{\text{ }}\hat{\rm W}^{{{\rm R} - {\rm R}}} \) that an increase in transfer price b, retail price decreases, and the collection rate increases. Demand (\(\phi - \beta p\)) can be increased via a reduction in the retail price and an increase in the collection rate reduces the manufacturing cost. Thus, \(\frac{{\partial \hat{\Pi }_{M}^{R - R} }}{\partial b} > 0\) and \(b = \Delta\).
Now, the optimal wholesale price, retail price, and retailer’s collection rate are obtained as,
Limitation \(0 \le \tau_{R}^{R - R*} < 1\) completes this section.
Appendix B
MR-M Model, manufacturer, and retailer hybrid collection: manufacturer Stackelberg
-
Problem of retailer
First, let’s investigate the concavity of the retailer profit function.
For the retailer profit function to be concave, the determinants of the above Hessian matrix have to be positive and negative decussate—i.e. \(\left| {H_{1} } \right| < 0, \, \left| {H_{2} } \right| > 0\). In this case, the retailer profit function will be concave compared to \(p^{MR - M} , \, \tau_{R}^{MR - M}\) with a unique optimal solution if \(4C_{L} > \beta (b - A)^{2}\). Now, the retailer’s optimal decisions are obtained by solving the following equations using the first-order condition.
The retailer’s optimal decisions will be as follows:
-
Problem of manufacturer
considering the retailer solutions and, \(Y = 4C_{L} - \beta (b - A)^{2}\) and \(S = (b - A)(\Delta - b)\), the manufacturer profit function will be as follows:
Now let us investigate the concavity of the manufacturer profit function,
For the manufacturer profit function to be concave compared to \(W^{MR - M} , \, \tau_{M}^{MR - M}\), the determinants of the minor of the hessian matrix are required to be negative and positive decussate. In this case, the Hessian matrix and manufacturer profit function will be negative and concave, respectively, if
The same as with the previous model, \(\frac{{\partial \Pi_{M}^{MR - R} }}{\partial b} > 0\) and \(b = \Delta\) in this model.
If \(8C_{L} > \beta \left[ {2(b - A)^{2} + 2(b - A)(\Delta - b) + (\Delta - A)^{2} } \right]\), the optimal wholesale price and manufacturer’s collection rate will be as follows,
Replacing \(W^{MR - M*}\) in \(\hat{p}^{MR - M}\) and \(\hat{\tau }_{M}^{MR - M}\) equations give the optimal wholesale price and retailer’s collection rate as,
Limitation \(0 \le \tau_{M}^{MR - M*} + \tau_{R}^{MR - M*} < 1\) completes this section.
MR-R Model, manufacturer, and retailer hybrid collection: retailer Stackelberg
-
Problem of manufacturer
given that the manufacturer profit function is incremental to the wholesale price, the wholesale price in this model will be as follows, which is the same as with the R-R Model (explained in “Appendix A” No. 2),
For the manufacturer’s collection rate, the second derivative of the manufacturer profit function is calculated due to the manufacturer’s collection rate as,
Given that \(\frac{{\partial^{2} \Pi_{M}^{MR - R} }}{{\partial (\tau_{M}^{MR - R} )^{2} }} < 0\), the manufacturer profit function will be concave, and the manufacturer’s collection rate is as follows,
-
Problem of retailer
Considering the manufacturer’s solutions, the retailer profit function is
Now, to investigate the concavity of the retailer profit function due to the wholesale price and retailer’s collection rate, its Hessian matrix is formed as,
If the above Hessian matrix is negative, the retailer profit function is concave. Thus, the retailer profit function will be concave with a unique optimal solution if
Now, let us obtain the retailer’s best reactions using the first-order condition as,
Replacing \(\hat{p}^{MR - R}\) in \(\hat{W}^{MR - R}\) and \(\hat{\tau }_{M}^{MR - R}\) equations give the wholesale price and manufacturer’s collection rate as,
The same as with the R-R Model in “Appendix A” and increase in b increases both the manufacturer’s collection rate and retailer’s collection rate and reduces both the retail price and wholesale price. The increased collection rates reduce manufacturing cost \(\overline{C} = C_{m} - \Delta \tau\) and the reduced cost increases the demand for the product. The increased demand and reduced manufacturing cost increase profit. Thus, the manufacturer gives the entire saving resulted from the manufacturing to the retailer. Hence, \(\frac{{\partial \Pi_{M}^{MR - R} }}{\partial b} > 0\) and \(b = \Delta\).
Now, the optimal decisions of the manufacturer and retailer will be,
Limitation \(0 \le \tau_{M}^{MR - R*} + \tau_{R}^{MR - R*} < 1\) completes this section.
Appendix C
M&R-M Model, manufacturer and retailer competitive collection: manufacturer Stackelberg
-
Problem of retailer
We need to first investigate the retailer profit function concavity to obtain equilibrium retailer decisions. Thus, we have
To investigate the retailer profit function concavity, we need to form its Hessian matrix as,
For the retailer profit function to be concave, the Hessian matrix should be negative: i.e. its determinants should be negative and positive decussate and \(\left| {H_{1} } \right| < 0, \, \left| {H_{2} } \right| > 0\). In this case, the retailer profit function will be concave compared to \(p^{M\& R - M} , \, \tau_{R}^{M\& R - M}\) with a unique optimal solution if \(4C_{L} > \beta (b - A)^{2} (1 - \alpha^{2} )\). Now, the retailer’s optimal decisions are obtained by using the first-order condition as,
-
Problem of manufacturer
Replacing \(\hat{p}^{M\& R - M}\) and \(\hat{\tau }_{M}^{M\& R - M}\) in the retailer profit function and considering \(Y = 4C_{L} - \beta (b - A)^{2} (1 - \alpha^{2} )\) and \(S = (b - A)(\Delta - b)\) gives the manufacturer profit function as
For the manufacturer problem to have a unique optimal solution, the manufacturer profit function has to be concave due to the wholesale price and manufacturer’s collection rate. Thus, we form the Hessian matrix of the manufacturer’s profit as,
If the Hessian matrix is negative and the manufacturer profit function is concave, then If \(8C_{L} > \beta (1 - \alpha^{2} )\left[ {2S + (b - A)^{2} (2 - \alpha ) + (\Delta - A)^{2} } \right]\), the manufacturer’s optimal decisions will be as follows,
As same as with the previous explanations, \(\frac{{\partial \Pi_{M}^{M\& R - R} }}{\partial b} > 0\) and \(b = \Delta\).
Replacing \(W^{MR - M*}\) in \(\hat{p}^{M\& R - M}\) and \(\hat{\tau }_{M}^{M\& R - M}\) equations give the optimal retail price and retailer’s collection rate as,
Limitation \(0 \le \tau_{M}^{M\& R - M*} + \tau_{R}^{M\& R - M*} < 1\) completes this section.
M&R-R Model, manufacturer, and retailer competitive collection: retailer Stackelberg
-
Problem of manufacturer
The same approach as with the previous retailer Stackelberg models is employed in this model. The wholesale price is as follows
Since concavity plays an important role in obtaining optimal decisions, the manufacturer profit function concavity according to the manufacturer’s collection rate is investigated.
\(\frac{{\partial^{2} \Pi_{M}^{M\& R - R} }}{{\partial (\tau_{M}^{M\& R - R} )^{2} }} < 0\) shows that the manufacturer profit function is concave due to the manufacturer’s collection rate. The manufacturer’s collection rate is,
-
Problem of retailer
given the manufacturer solutions, the retailer profit function will be as follows,
Since concavity plays an important role in obtaining optimal decisions, its Hessian matrix is formed as follows to investigate the retailer profit function concavity due to the retail price and retailer’s collection rate:
If the determinants of the Hessian matrix are negative and positive decussate (i.e.\(\left| {H_{1} } \right| < 0, \, \left| {H_{2} } \right| > 0\)), the retailer profit function is concave. Thus, the retailer profit function will be concave with a unique optimal solution if
Now, the following equations are solved using the first-order condition, obtaining the retailer’s best reactions.
Replacing \(p^{M\& R - R*}\) in \(\hat{W}^{M\& R - R}\) and \(\hat{\tau }_{M}^{M\& R - R}\) equations give the optimal wholesale price and manufacturer’s collection rate as
The same with the previous models, this model gives the entire saving resulted from remanufacturing \(\Delta\) to the retailer, and thus \(\frac{{\partial \Pi_{M}^{M\& R - R} }}{\partial b} > 0\) and \(b = \Delta\).
Limitation \(0 \le \tau_{M}^{M\& R - R*} + \tau_{R}^{M\& R - R*} < 1\) completes the proof of this section.
Rights and permissions
About this article
Cite this article
Sahebi, H., Ranjbar, S. & Teymouri, A. Investigating different reverse channels in a closed-loop supply chain: a power perspective. Oper Res Int J 22, 1939–1985 (2022). https://doi.org/10.1007/s12351-021-00645-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12351-021-00645-2