Skip to main content

Advertisement

Springer Nature Link
Log in

A variable neighborhood search for the budget-constrained maximal covering location problem with customer preference ordering

  • Original Paper
  • Published:
Operational Research Aims and scope Submit manuscript

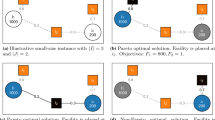
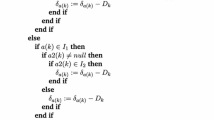Abstract

This paper introduces a variant of Maximal Covering Location Problem (MCLP) with customer preference ordering and limited budget for establishing facilities. It is assumed that a set of facilities belonging to competitors are already present at the market. Customers are free to choose among facilities located within a given coverage radius, according to their preferences. Instead of fixed number of facilities to be located, the new problem assumes limited budget for establishing the network of facilities of the considered firm. The goal is to choose optimal locations for opening facilities and find optimal allocations of customers to opened facilities, such that the covered demand of customers is maximized. The newly introduced variant of MCLP is formulated as an integer linear program. As we are dealing with an NP-hard optimization problem, an efficient Variable Neighborhood Search (VNS) is proposed as solution approach. In addition, the effects of incorporating strategies of accepting a worse solution or exploring neighborhood of an infeasible solution in the VNS framework were investigated. Computational results on modified MCLP instances from the literature show that VNS quickly reaches optimal solutions or improves lower bounds obtained by exact Gurobi solver. The advantages of VNS over Gurobi solver are more obvious on newly generated large-scale MCLP instances, especially in cases when Gurobi fails to provide a feasible solution. The proposed VNS is additionally tested on modified real-world MCLP instances, and the obtained results clearly indicate its capacity to solve realistic-sized test examples in short running times.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Aksen D, Piyade N, Aras N (2010) The budget constrained r-interdiction median problem with capacity expansion. Cent Eur J Oper Res 18(3):269–291

    Article  Google Scholar 

  • Alekseeva E, Kochetov Y (2007) Genetic local search for the p-median problem with clients’ preferences. Diskret Anal Issled Oper 14:3–31

    Google Scholar 

  • Berman O, Krass D (2002) The generalized maximal covering location problem. Comput Oper Res 29(6):563–581

    Article  Google Scholar 

  • Camacho-Vallejo J, Cordero-Franco A, González-Ramírez R (2014) Solving the bilevel facility location problem under preferences by a Stackelberg-evolutionary algorithm. Math Probl Eng. https://doi.org/10.1155/2014/430243

    Article  Google Scholar 

  • Cánovas L, García S, Labbé M, Marín A (2007) A strengthened formulation for the simple plant location problem with order. Oper Res Lett 35(2):141–150

    Article  Google Scholar 

  • Casas-Ramírez M, Camacho-Vallejo J (2017) Solving the p-median bilevel problem with order through a hybrid heuristic. Appl Soft Comput 60:73–86

    Article  Google Scholar 

  • Casas-Ramírez MS, Camacho-Vallejo JF, Díaz JA, Luna DE (2017) A bi-level maximal covering location problem. Oper Res Int J 20:827–855

    Article  Google Scholar 

  • Chekuri C, Kumar A (2004) Maximum coverage problem with group budget constraints and applications. Algorithms and techniques. In: Jansen K, Khanna S, Rolim JDP, Ron D (eds) Approximation, randomization, and combinatorial optimization. Springer, Heidelberg, pp 72–83

    Chapter  Google Scholar 

  • Church R (1984) The planar maximal covering location problem. J Reg Sci 24(2):185–201

    Article  Google Scholar 

  • Church R, ReVelle C (1974) The maximal covering location problem. Pap Reg Sci 32(1):101–118

    Article  Google Scholar 

  • Cohen R, Katzir L (2008) The generalized maximum coverage problem. Inform Process Lett 108(1):15–22

    Article  Google Scholar 

  • Colombo F, Cordone R, Lulli G (2015) A variable neighborhood search algorithm for the multimode set covering problem. J Global Optim 63(3):461–480

    Article  Google Scholar 

  • Colombo F, Cordone R, Lulli G (2016) The multimode covering location problem. Comput Oper Res 67:25–33

    Article  Google Scholar 

  • Davari S, Zarandi MHF, Turksen IB (2013) A greedy variable neighborhood search heuristic for the maximal covering location problem with fuzzy coverage radii. Knowl Based Syst 41:68–76

    Article  Google Scholar 

  • Díaz JA, Luna DE, Camacho-Vallejo JF, Casas-Ramírez MS (2017) GRASP and hybrid GRASP-Tabu heuristics to solve a maximal covering location problem with customer preference ordering. Expert Syst Appl 82:67–76

    Article  Google Scholar 

  • Drakulić D, Takači A, Marić M (2016) New model of maximal covering location problem with fuzzy conditions. Comput Inform 35(3):635–652

    Google Scholar 

  • Duque PAM, Coene S, Goos P, Sörensen K, Spieksma F (2013) The accessibility arc upgrading problem. Eur J Oper Res 224(3):458–465

    Article  Google Scholar 

  • Farahani RZ, Asgari N, Heidari N, Hosseininia M, Goh M (2012) Covering problems in facility location: a review. Comput Ind Eng 62(1):368–407

    Article  Google Scholar 

  • Glover F, Hao JK (2011) The case for strategic oscillation. Ann Oper Res 183(1):163–173

    Article  Google Scholar 

  • Gorbachevskaya L (1998) Polynomially solvable and NP-hard bilevel standardization problems. PhD Thesis (in Russian), Sobolev Institute of Mathematics, Novosibirsk

  • Hanjoul P, Peeters D (1987) A facility location problem with clients’ preference ordering. Reg Sci Urb Econ 17:451–473

    Article  Google Scholar 

  • Hansen H, Kochetov Y, Mladenović N (2004) Lower bounds for the uncapacitated facility location problem with user preferences. Preprint G-2004-24, GERAD-HEC, Montreal

  • Hansen P, Mladenović N (2014) Variable neighborhood search. In: Burke EK, Graham RD (eds) Search methodologies: introductory tutorials in optimization and decision support techniques. Springer, New York, pp 313–337

    Chapter  Google Scholar 

  • Hansen P, Mladenović N, Pérez JAM (2010) Variable neighbourhood search: methods and applications. Ann Oper Res 175(1):367–407

    Article  Google Scholar 

  • Hansen P, Mladenović N, Todosijević R, Hanafi S (2017) Variable neighborhood search: basics and variants. EURO J Comput Optim 5(3):423–454

    Article  Google Scholar 

  • Hansen P, Mladenović N, Brimberg J, Pérez JAM (2019) Variable neighborhood search. In: Potvin JY, Gendreau M (eds) Handbook of metaheuristics. Springer, Berlin, pp 57–97

    Chapter  Google Scholar 

  • Ishii H, Lee YL, Yeh KY (2007) Fuzzy facility location problem with preference of candidate sites. Fuzzy Sets Syst 158(17):1922–1930

    Article  Google Scholar 

  • Janković O, Mišković S, Stanimirović Z, Todosijević R (2017) Novel formulations and VNS-based heuristics for single and multiple allocation p-hub maximal covering problems. Ann Oper Res 259(1–2):191–216

    Article  Google Scholar 

  • Jia H, Ordóñez F, Dessouky MM (2007) Solution approaches for facility location of medical supplies for large-scale emergencies. Comput Ind Eng 52(2):257–276

    Article  Google Scholar 

  • Khuller S, Moss A, Naor JS (1999) The budgeted maximum coverage problem. Inform Process Lett 70(1):39–45

    Article  Google Scholar 

  • Lee JM, Lee YH (2012) Facility location and scale decision problem with customer preference. Comput Ind Eng 63(1):184–191

    Article  Google Scholar 

  • Lust T, Tuyttens D (2014) Variable and large neighborhood search to solve the multiobjective set covering problem. J Heuristics 20(2):165–188

    Article  Google Scholar 

  • Macedo R, Alves C, Hanafi S, Jarboui B, Mladenović N, Ramos B, de Carvalho JV (2015) Skewed general variable neighborhood search for the location routing scheduling problem. Comput Oper Res 61:143–152

    Article  Google Scholar 

  • Marić M, Stanimirović Z, Milenković N, Djenić A (2015) Metaheuristic approaches to solving large-scale bilevel uncapacitated facility location problem with clients’ preferences. Yugosl J Oper Res 25(3):361–368

    Article  Google Scholar 

  • Máximo VR, Nascimento MC, Carvalho AC (2017) Intelligent-guided adaptive search for the maximum covering location problem. Comput Oper Res 78:129–137

    Article  Google Scholar 

  • Megiddo N, Zemel E, Hakimi SL (1983) The maximum coverage location problem. SIAM J Algebra Discrete 4(2):253–261

    Article  Google Scholar 

  • Mišković S (2017) A VNS-LP algorithm for the robust dynamic maximal covering location problem. OR Spectr 39(4):1011–1033

    Article  Google Scholar 

  • Mladenović N, Hansen P (1997) Variable neighborhood search. Comput Oper Res 24(11):1097–1100

    Article  Google Scholar 

  • Mrkela L, Stanimirović Z (2018) VNS-based solution approaches to the maximal covering location problem with customer preference ordering. In: Urošević D, Vidović M, Makajić-Nikolić D (eds) Proceedings of the XIII Balkan conference on operational research, BALCOR 2018, The Mathematical Institute of the Serbian Academy of Sciences and Arts (SANU), Belgrade, Serbia, pp. 133–140

  • Rajagopalan HK, Saydam C, Xiao J (2008) A multiperiod set covering location model for dynamic redeployment of ambulances. Comput Oper Res 35(3):814–826

    Article  Google Scholar 

  • ReVelle C, Hogan K (1989) The maximum availability location problem. Transp Sci 23(3):192–200

    Article  Google Scholar 

  • ReVelle C, Schweitzer J, Snyder S (1996) The maximal conditional covering problem. INFOR 34(2):77–91

    Google Scholar 

  • Salari M (2014) An iterated local search for the budget constrained generalized maximal covering location problem. J Math Model Algorithm Oper Res 13(3):301–313

    Article  Google Scholar 

  • Schmid V, Doerner KF (2010) Ambulance location and relocation problems with time-dependent travel times. Eur J Oper Res 207(3):1293–1303

    Article  Google Scholar 

  • Snyder LV (2011) Covering problems. In: Eiselt HA, Marianov V (eds) Foundations of location analysis. International series in operations research and management science. Springer, Boston, pp 109–135

    Google Scholar 

  • Stanimirović Z, Mišković S, Trifunović D, Veljović V (2017) A two-phase optimization method for solving the multi-type maximal covering location problem in emergency service networks. Inf Technol Control 46(1):100–117

    Google Scholar 

  • Vasilyev I, Klimentova X, Kochetov Y (2009) New lower bounds for the facility location problem with clients’ preferences. Comp Math Math Phys 49:1010–1020

    Article  Google Scholar 

  • Vasilyev I, Klimentova X, Maurizio B (2013) Polyhedral study of simple plant location problem with order. Oper Res Lett 41(2):153–158

    Article  Google Scholar 

  • Watson-Gandy C (1982) Heuristic procedures for the m-partial cover problem on a plane. Eur J Oper Res 11(2):149–157

    Article  Google Scholar 

  • White JA, Case KE (1974) On covering problems and the central facilities location problem. Geogr Anal 6(3):281–294

    Article  Google Scholar 

  • Zarandi MHF, Davari S, Sisakht SAH (2013) The large-scale dynamic maximal covering location problem. Math Comput Model 57(3–4):710–719

    Article  Google Scholar 

Download references

Funding

The authors state that the research conducted in this paper was partially supported by Serbian Ministry of Education, Science and Technological Development under the Grant No. 174010.

Author information

Authors and Affiliations

  1. Faculty of Information Technology, Belgrade Metropolitan University, Tadeuša Košćuška 63, 11000, Belgrade, Serbia

    Lazar Mrkela

  2. Faculty of Mathematics, University of Belgrade, Studentski trg 16/IV, 11 000, Belgrade, Serbia

    Zorica Stanimirović

Authors
  1. Lazar Mrkela
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zorica Stanimirović
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Lazar Mrkela.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mrkela, L., Stanimirović, Z. A variable neighborhood search for the budget-constrained maximal covering location problem with customer preference ordering. Oper Res Int J 22, 5913–5951 (2022). https://doi.org/10.1007/s12351-021-00652-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12351-021-00652-3

Keywords

Mathematics Subject Classification