Vehicle routing problem under safe separation distance for multiple unmanned aerial vehicle operation

Abstract

In this work, we present a variant of the vehicle routing problem for multiple unmanned aerial vehicle operation. The problem was described as a multi-depot vehicle routing problem with separation distance constraints, and two mathematical models were developed to find the best routes under capacity, maximum traveling time, and intervehicle separation constraints. In the first model, the separation distance constraint was proposed using a discrete time window based on previous studies, while the second model restricts the relative difference of departure time between every two arcs within the safety distance. Although the second model was designed using the mixed-integer linear programming model, finding acceptable solutions within a limited computation time was a challenge. Therefore, a decomposition heuristic, which divides the second model into a routing step followed by a scheduling step, and a hybrid tabu search algorithm with constructive initial solution generation were suggested. The performance of the suggested algorithms was evaluated for randomly generated graphs in two-dimensional space, and computational experiments showed that the proposed algorithms can be applied to practical cases with enhanced computational efficiency.

Appendix

1.1 Proof: ${{\varvec{H}}}_{{\varvec{i}}{\varvec{j}}{{\varvec{i}}}^{\boldsymbol{^{\prime}}}{{\varvec{j}}}^{\boldsymbol{^{\prime}}}}$ is a convex set in ${\mathbb{R}}^{+}$

Let $\delta$ be the departure time difference between arcs $\left(i,j\right)$ and $\left({i}{^{\prime}},{j}{^{\prime}}\right)$, which is assumed to be in ${\mathbb{R}}^{+}$. Also, we assume that the departure time of arc $\left(i,j\right)$ is 0.

• 1) Time range

  Let ${T}_{ij{i}{^{\prime}}{j}{^{\prime}}}\left(\delta \right)\in T$ be the time range in which both vehicles exist on the arcs concurrently when the vehicle on arc $\left({i}{^{\prime}},{j}{^{\prime}}\right)$ depart from node ${i}{^{\prime}}$ at $\delta$. If one vehicle on arc $\left(i,j\right)$ departs from node $i$ at time $0$, it completes the service at node $j$ at time $\left({C}_{ij}+{S}_{j}\right)$, and the other vehicle on arc $\left({i}{^{\prime}},{j}{^{\prime}}\right)$ starts and finishes at time $\delta$ and $\left({C}_{{i}{^{\prime}}{j}{^{\prime}}}+{S}_{{j}{^{\prime}}}+\delta \right)$, respectively. Equation (A1) is the definition of ${T}_{ij{i}{^{\prime}}{j}{^{\prime}}}\left(\delta \right)$ for every $\left\{\left(i,j\right),\left({i}{^{\prime}},{j}{^{\prime}}\right)\right\}\in P$.

  $${T}_{ij{i}{^{\prime}}{j}{^{\prime}}}\left(\delta \right)=\left\{t |t\in T, \delta \le t\le \mathrm{min}\left({C}_{ij}+{S}_{j},{C}_{{i}{^{\prime}}{j}{^{\prime}}}+{S}_{{j}{^{\prime}}}+\delta \right)\right\}$$

  (A1)

• 2) Euclidean distance

  The 2D locations of the vehicles on arcs $\left(i,j\right)$ and $\left({i}{^{\prime}},{j}{^{\prime}}\right)$ at time $t\in {T}_{ij{i}{^{\prime}}{j}{^{\prime}}}\left(\delta \right)$ are suggested to be (${L}_{ij}^{X}\left(\delta ,t\right),{L}_{ij}^{Y}\left(\delta ,t\right),{L}_{ij}^{Z}\left(\delta ,t\right)$) and (${L}_{{i}{^{\prime}}{j}{^{\prime}}}^{X}\left(\delta ,t\right),{L}_{{i}{^{\prime}}{j}{^{\prime}}}^{Y}\left(\delta ,t\right),{L}_{{i}{^{\prime}}{j}{^{\prime}}}^{Z}\left(\delta ,t\right)$) in Eqs. (A2) and (A3), respectively. Each location function is divided into two cases since it is assumed that every vehicle stays at the customer node during its service time.

  $$\left({L}_{ij}^{X}\left(\delta ,t\right),{L}_{ij}^{Y}\left(\delta ,t\right),{L}_{ij}^{Z}\left(\delta ,t\right)\right)=\left\{\begin{array}{cc}\left({L}_{i}^{X}+{V}_{ij}^{X}t,{L}_{i}^{Y}+{V}_{ij}^{Y}t,{L}_{i}^{Z}+{V}_{ij}^{Z}t\right)& if \, t\le {C}_{ij}\\ \left({L}_{j}^{X}, {L}_{j}^{Y}, {L}_{j}^{Z}\right)& o.w.\end{array}\right.$$

  (A2)
  $$\left({L}_{{i}{^{\prime}}{j}{^{\prime}}}^{X}\left(\delta ,t\right),{L}_{{i}{^{\prime}}{j}{^{\prime}}}^{Y}\left(\delta ,t\right),{L}_{{i}{^{\prime}}{j}{^{\prime}}}^{Z}\left(\delta ,t\right)\right)=\left\{\begin{array}{cc}\left({L}_{{i}{^{\prime}}}^{X}+{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{X}\left(t-\delta \right),{L}_{{i}{^{\prime}}}^{Y}+{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{Y}\left(t-\delta \right),{L}_{{i}{^{\prime}}}^{Z}+{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{Z}\left(t-\delta \right)\right)& if \, t-\delta \le {C}_{{i}{^{\prime}}{j}{^{\prime}}}\\ \left({L}_{{j}{^{\prime}}}^{X}, {L}_{{j}{^{\prime}}}^{Y}, {L}_{{j}{^{\prime}}}^{Z}\right)& o.w.\end{array}\right.$$

  (A3)

  The Euclidean distance between two vehicles at every time $t\in {T}_{ij{i}{^{\prime}}{j}{^{\prime}}}\left(\delta \right)$ is denoted by ${E}_{ij{i}{^{\prime}}{j}{^{\prime}}}\left(\delta ,t\right)={\Vert \left({L}_{ij}^{X}\left(\delta ,t\right),{L}_{ij}^{Y}\left(\delta ,t\right),{L}_{ij}^{Z}\left(\delta ,t\right)\right)-\left({L}_{{i}{^{\prime}}{j}{^{\prime}}}^{X}\left(\delta ,t\right),{L}_{{i}{^{\prime}}{j}{^{\prime}}}^{Y}\left(\delta ,t\right),{L}_{{i}^{{\prime}}{j}{^{\prime}}}^{Z}\left(\delta ,t\right)\right)\Vert }_{2}$, and Eq. (A4) shows the details of ${E}_{ij{i}{^{\prime}}{j}{^{\prime}}}\left(\delta ,t\right)$ under the consideration of staying for service at the end node on each arc.

  $${E}_{ij{i}{^{\prime}}{j}{^{\prime}}}{\left(\delta ,t\right)}^{2}= \left\{\begin{array}{l}\begin{array}{ll}{\left\{{L}_{i}^{X}+{V}_{ij}^{X}t-{L}_{{i}{^{\prime}}}^{X}-{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{X}\left(t-\delta \right)\right\}}^{2}+{\left\{{L}_{i}^{Y}+{V}_{ij}^{Y}t-{L}_{{i}{^{\prime}}}^{Y}-{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{Y}\left(t-\delta \right)\right\}}^{2}\\ \quad+{\left\{{L}_{i}^{Z}+{V}_{ij}^{Z}t-{L}_{{i}{^{\prime}}}^{Z}-{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{Z}\left(t-\delta \right)\right\}}^{2}\quad \mathrm{if} \, t < \mathrm{min}\left({C}_{ij},{C}_{{i}{^{\prime}}{j}{^{\prime}}}+\delta \right)\\ {\left\{{L}_{j}^{X}-{L}_{{i}{^{\prime}}}^{X}-{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{X}\left(t-\delta \right)\right\}}^{2}+{\left\{{L}_{j}^{Y}-{L}_{{i}{^{\prime}}}^{Y}-{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{Y}\left(t-\delta \right)\right\}}^{2}\\ \quad+{\left\{{L}_{j}^{Z}-{L}_{{i}{^{\prime}}}^{Z}-{V}_{{i}{^{\prime}}{j}{^{\prime}}}^{Z}\left(t-\delta \right)\right\}}^{2}\quad \mathrm{if} \, {C}_{ij}\le t < {C}_{{i}{^{\prime}}{j}{^{\prime}}}+\delta \end{array}\\ \begin{array}{ll}{\left\{{L}_{i}^{X}+{V}_{ij}^{X}t-{L}_{{j}{^{\prime}}}^{X}\right\}}^{2}+{\left\{{L}_{i}^{Y}+{V}_{ij}^{Y}t-{L}_{{j}{^{\prime}}}^{Y}\right\}}^{2}\\ \quad+{\left\{{L}_{i}^{Z}+{V}_{ij}^{Z}t-{L}_{{j}{^{\prime}}}^{Z}\right\}}^{2}\quad \mathrm{if} \, {C}_{{i}{^{\prime}}{j}{^{\prime}}}+\delta \le t<{C}_{ij}\\ {\left\{{L}_{J}^{X}-{L}_{{j}{^{\prime}}}^{X}\right\}}^{2}+{\left\{{L}_{j}^{Y}-{L}_{{j}{^{\prime}}}^{Y}\right\}}^{2}\\ \quad+{\left\{{L}_{j}^{Z}-{L}_{{j}{^{\prime}}}^{Z}\right\}}^{2}\quad \mathrm{if} \mathrm{max}\left({C}_{ij},{C}_{{i}{^{\prime}}{j}{^{\prime}}}+\delta \right)\le t\end{array}\end{array}\right.$$

  (A4)

• 3) Infeasible range of the departure time difference

  The departure time difference $\delta$ is in ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}$ if there exists a time $t\in {T}_{ij{i}{^{\prime}}{j}^{{\prime}}}\left(\delta \right)$ where ${E}_{ij{i}{^{\prime}}{j}{^{\prime}}}\left(\delta ,t\right)$ is less than the safety distance, $B$. Equation (A5) below is the definition of ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}$, which is the union of partial infeasible ranges:

  $${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}=\left\{\delta | {E}_{ij{i}{^{\prime}}{j}{^{\prime}}}{\left(\delta ,*\right)}^{2}=\underset{t\in {T}_{\mathit{ij}{i}{^{\prime}}{j}{^{\prime}}}\left(\delta \right)}{\mathrm{min}}\left\{{E}_{ijij}{\left(\delta ,t\right)}^{2}\right\}<{B}^{2}\right\}$$
  $$={H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}\cup {H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(2\right)}\cup {H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(3\right)}\cup {H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(4\right)}$$

  (A5)
  $${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}=\left\{\delta | {E}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}{\left(\delta ,*\right)}^{2}=\underset{\delta \le t<\mathrm{min}\left({C}_{\mathit{ij}},{C}_{{i}{^{\prime}}{j}{^{\prime}}}+\delta \right)}{\mathrm{min}}\left\{{E}_{ijij}{\left(\delta ,t\right)}^{2}\right\}<{B}^{2}\right\}$$

  (A6)
  $${H}_{ij{i}^{{\prime}}{j}{^{\prime}}}^{\left(2\right)}=\left\{\delta | {E}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(2\right)}{\left(\delta ,*\right)}^{2}=\underset{{C}_{\mathit{ij}}\le t<{C}_{{i}{^{\prime}}{j}{^{\prime}}}+\delta }{\mathrm{min}}\left\{{E}_{ijij}{\left(\delta ,t\right)}^{2}\right\}<{B}^{2}\right\}$$

  (A7)
  $${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(3\right)}=\left\{\delta |{E}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(3\right)}{\left(\delta ,*\right)}^{2}=\underset{{C}_{{i}{^{\prime}}{j}{^{\prime}}}+\delta \le t<{C}_{\mathit{ij}}}{\mathrm{min}}\left\{{E}_{ijij}{\left(\delta ,t\right)}^{2}\right\}<{B}^{2}\right\}$$

  (A8)
  $${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(4\right)}=\left\{\delta | {E}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(4\right)}{\left(\delta ,*\right)}^{2}=\underset{\mathrm{max}\left({C}_{\mathit{ij}},{C}_{{i}{^{\prime}}{j}{^{\prime}}}+\delta \right)\le t<\mathrm{min}\left({C}_{\mathit{ij}}+{S}_{j},{C}_{{i}{^{\prime}}{j}{^{\prime}}}+{S}_{{j}{^{\prime}}}+\delta \right)}{\mathrm{min}}\left\{{E}_{ijij}{\left(\delta ,t\right)}^{2}\right\}<{B}^{2}\right\}$$

  (A9)

• 4) Convexity of the infeasible range

Since ${E}_{ijij}^{\left(n\right)}{\left(\delta ,t\right)}^{2}$ for every $n\in \left\{\mathrm{1,2},\mathrm{3,4}\right\}$ in equations (A6)–(A9) is the polynomial function of $\delta$ and $t$, all partial infeasible ranges are a convex set of $\delta$, denoted as ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}=\left({F}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)},{G}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}\right)$ for every $n\in \left\{\mathrm{1,2},\mathrm{3,4}\right\}$.

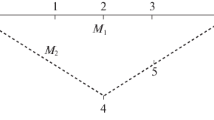
Let ${\Delta }_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}$ be the subset of ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}$ with a minimum value of the Euclidean distance function, ${\Delta }_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}=\underset{\delta }{\mathrm{argmin}}\left\{{E}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}{\left(\delta ,*\right)}^{2} | \delta \in {H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}\right\}$, and ${\delta }_{\mathrm{min}}^{\left(n\right)}$ be the minimum value of $\delta$ in ${\Delta }_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}$, ${\delta }_{\mathrm{min}}^{\left(n\right)}=\mathrm{min}\left\{{\Delta }_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(n\right)}\right\},\mathrm{ for every }n\in \left\{\mathrm{1,2},\mathrm{3,4}\right\}$. Below Fig. A1, which is an illustration of ${\delta }_{\mathrm{min}}^{\left(2\right)}$, ensures that ${\delta }_{\mathrm{min}}^{\left(2\right)}$ is in ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}$ if both ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}$ and ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(2\right)}$ are not empty sets. Since both ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}$ and ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(2\right)}$ are convex sets, ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}\cup {H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(2\right)}$ is also a convex set. It can be affirmed similarly that ${\delta }_{\mathrm{min}}^{\left(3\right)}$ and ${\delta }_{\mathrm{min}}^{\left(4\right)}$ are in ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}$; therefore, ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}={H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}\cup {H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(2\right)}\cup {H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(3\right)}\cup {H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(4\right)}$ is a convex set of $\delta$ in ${\mathbb{R}}^{+}$. ■

Fig. A1

A brief illustration that ${\delta }_{\mathrm{min}}^{\left(2\right)}$ is in ${H}_{ij{i}{^{\prime}}{j}{^{\prime}}}^{\left(1\right)}$