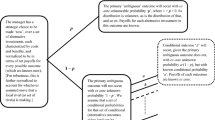
Abstract
Strategic decision-making is one of the most important functions of the manager. These decision problems, however, are made much more challenging when they are plagued by ambiguity and interdependencies with rivals. In fact, irreducible ambiguity makes traditional optimization techniques inapplicable, leaving a manager to struggle to identify an approach to use to generate higher payoffs. While a literature on addressing ambiguity exists in the behavioral realm and when it is converted to the equivalent of risk under subjective beliefs, a gap remains when ambiguity is left as unknowable. We address that gap here by considering these problems in a game-theoretical structure in order to address three related and relevant research questions: When does ambiguity matter in such problems? How much does that ambiguity matter (i.e., how costly is it)? What kind of approach or heuristic might help improve payoffs in such problems? We use computational simulation to provide the answers. We discuss the implications.


Similar content being viewed by others
Data Availability
code for the Excel simulation and data made available as per Journal requirements [or by request].
Code Availability
code for the Excel simulation and data made available as per Journal requirements [or by request].
Notes
We note that the Ellsberg (1961) version of ambiguity is not the only characterization, but it is the simplest and most standard and tested. We provide our Ellsberg-consistent basic model as a benchmark that cannot only provide new insights but also can be built on in a straightforward manner in the future. That said, we also acknowledge that the term ‘ambiguity’ has been defined differently in other literature, specifically that involving communications issues, where it refers to an outcome of linguistic confusion on the part of the receiver of a message (i.e., where there is some equivocality in at least two possible interpretations of that message). However, in the context of the uncertainty literature – the context of this study – we consider its definition to be clear, in that it refers to Ellsberg’s (1961) conceptualization (i.e., where probabilities of possible outcome states are unknown). We are comfortable in this assertion because much of the recent SDMUA research also applies this definition to the term (e.g., Dequech 2011; Etner et al. 2012; Holm et al. 2013; Packard et al. 2017; and, Townsend et al. 2018).
Two points on these assertions. First, it is possible that ambiguity can matter in terms of a rational decision choice for one player but not for the other [player 1 can be locked into U, but player 2 will differ in choice between L and R depending on the value of p]. Second, the payoff variance in cases where ambiguity does not matter to decisions is about 20-percent lower to a player than where ambiguity does matter to both players and, in terms of relative variance [i.e., variance divided by average payoff] it is about one-sixth [of the ratio of when ambiguity does matter to both players]. Such sizable differences in those payoff variance measures provide one way to assess the relative cost of ambiguity. Ambiguity appears to be quite costly in terms of adding to the relative noise of the payoffs (in both absolute and relative terms) and, given most decision-makers are variance-averse, that translates into decreased utility.
In such cases, the asymmetry can have a significant positive effect on average payoff. One reason is that the payoff structure is biased towards the player with the consistently dominant strategy (a bias that makes it consistently dominant). The other reason comes from our simulated playing of such cases across their hybrids. While, due to the ambiguity, we cannot predict the rival’s choice, when we assume a reasonable heuristic – like maximin – then we can calculate the average payoffs across the hybrids for the cases for each player and compare. Doing so reveals that the player not confronting the ambiguity can expect over twice the average payoff as her rival. (Given the distribution of p is unknowable for any case while such a calculation assumes a uniform distribution, this comparison should be taken with caution.)
The problem of justifying what to assume the other player is using as a heuristic is not obvious in such cases. That is why tournaments of computer algorithms and across human subjects are valuable (e.g., to identify tit-for-tat as a best strategy for the repeated prisoner’s dilemma game). Given this is not the paper for that kind of extended analysis, we choose the simplest approach to that problem – i.e., by assuming symmetry of choice of the heuristic.
All references to statistically significance refer to a two-tailed t-test of the means of the two measures, assuming unequal variance, where significance is at the 5-percent level. The average payoff comparisons were based on computing and recording the average payoff per case for each approach, then running means tests of one approach versus another based on that recorded payoff data (and then comparing relative mean levels when the means were the same sign). Cases were also categorized by the number of Nash equilibrium variants existed so that those means comparison tests could also be run by category.
These computations involved comparing average payoff levels per case. When the risk-equivalent payoff level for a case was lower than that of another approach, it was recorded. Then those events were divided by the total applicable cases to compute the percentages reported.
Comparing the cases when the coin-flip strategy did best (i.e., scored the highest average payoff in a case) to when the other heuristics did best reveals that these were not only substantially fewer in number but also the winning margin was about a third of the others.
We assume that parties cannot alter the game payoffs or affect the unknowability or bounds of p directly. If either is possible, however, then the attraction and possibility of those alternatives need to be considered as well. For example, if a third-party is affected by the game’s outcome, it may choose to affect a player’s payoff level (e.g., through subsidy or penalty/taxation, as Brander and Spencer [1985] depict in strategic trade policy).
If possible, the manager could also appeal to any affected third-party to try to alter the game to decrease the ambiguity for the manager’s benefit. Similarly, for policy-makers who are responsible for, or otherwise representative of, such third-parties, they could offer assistance to the managers that request (or should request) such intervention when feasible, legal and beneficial (e.g., when the manager’s firm’s payoffs from the game have positive social spillovers, like employment opportunities, technological knowledge sharing, and community-building). For example, if the game represents competitive pre-commitments when facing two future possible worlds (e.g., of a standards war or a new regulation) where ambiguity over that outcome is unknowable ex ante, then the manager might appeal to suppliers involved in each standard to offer more flexible contracts to diffuse the costs of her own ambiguous decision.
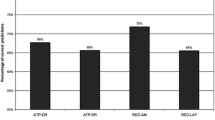
While it is difficult to repeat this simulated study in the real world, we can share some supporting but limited experimental results based on human subjects playing three SDMUA games (i.e., ones structured as this paper illustrates). We provide such results to begin to address some of the application limitations of simulations described above, and in an initial attempt to bolster our assertion that simulations are useful in analyzing SDMUA problems and testing some possible approaches to them. We recorded the play of real participants through a survey who were filtered for minimum expertise in relevant game-play. Participants were asked to choose their best options in three different SDMUA games (i.e., with option choices of U, D, or Mix of U and D), and to identify the rationale for each choice (from a limited list that included maximin). Three of the preliminary results are relevant here: First, one the SDMUA games in the survey was of the non-true SDMUA type – i.e., where the future state was ambiguous but not the dominant strategy. A majority of participants recognized this, but still a non-trivial minority (i.e., over a tenth) did not. This supports the insight of this present paper that such SDMUA types can catch decision-makers off-guard, and so the idea of training managers to identify such situations and choose the best strategy is valuable. Second, the two true SDMUA games used in the survey differed in complexity (i.e., in the number of transitions of Nash equilibria across the p-values), and the participants showed increased confusion over picking a preferred strategy as that complexity increased. This result supports the idea that increased ambiguity entails increased costs (at least of effort to get to a choice and to finding a consistent rationale to support that choice), and that ambiguity matters in presence and in level. In other words, the SDMUA problem comes in different variants, as the simulation showed, and those variants affect behaviors. Third, the second of the two true SDMUA games entailed a clear maximin choice. In the simulation that was referred to as strategic maximin, and participants chose this rationale – with the correct option – nearly a fifth of the time. This supports the analysis of this strategy in our simulation as one of the possible and interesting approaches to SDMUA games. (Further, it appears that playing that strategy against the ‘average’ rival would have been effective. When averaging the choices across all participants for that game, playing the maximin strategy would have hypothetically beaten the average choice in terms of relative payoffs.) This result helps put the example strategy analysis done in the simulation in a clearer perspective.
That is not to suggest that there are not rigorous ways to deal with the some of the challenges that ambiguity generates otherwise. For example, work in fuzzy sets (e.g., Zadeh 1978), in information gap analysis (e.g., Ben-Haim 2006), and in identifying the variance of the possible outcomes of ambiguous decisions (e.g., Machina 2014) are also very valuable.
References
Axelrod R (1984) The Evolution of Cooperation. Basic Books
Bajtelsmit V, Coats J, Thistle P (2015) The effect of ambiguity on risk management choices: An experimental study. J Risk & Uncertainty 50(3):249–280
Becker SW, Brownson F (1964) What price ambiguity? Or the role of ambiguity in decision making. J Pol Econ 72:62–73
Ben-Haim Y (2006) Info-gap decision theory: decisions under severe uncertainty. Elsevier
Bradbury MA, Hens T, Zeisberger S (2015) Improving investment decisions with simulated experience. Rev Finance 19(3):1019–1052
Brander JA, Spencer BJ (1985) Export subsidies and international market share rivalry. J Intl Econ 18(1–2):83–100
Casadesus MR, Zhu F (2013) Business model innovation and competitive imitation: The case of sponsor-based business models. Strat Man J 34(4):464–482
Cerreia-Vioglio S, Maccheroni F, Marinacci M, Montrucchio L (2013) Ambiguity and robust statistics. J Econ Theory 148(3):974–1049
Curley SP, Yates JF (1985) The center and range of the probability interval as factors affecting ambiguity preferences Org. Beh. Human Dec. Proc. 36:273–287
Dekel E, Lipman BL, Rustichini A (1998) Recent developments in modeling unforeseen contingencies. Eur Econ Rev 42(3–5):523–542
Dequech D (2011) Uncertainty: A typology and refinements of existing concepts. J Econ Issues 45:621–640
Dimov D (2018) Uncertainty under entrepreneurship. In: Fayolle A, Ramoglou S, Karatas-Ozkan M, Nicolopoulou K (eds) Philosophical reflexivity and entrepreneurship research. Routledge, pp 184–196
Einhorn HJ, Hogarth RM (1986) Decision making under ambiguity. The J Bus 59(4):S225–S250
Ellsberg D (1961) Risk, Ambiguity, and the Savage Axioms. Qtrly J Econ 75(4):643–669
Ellsberg D (1963) Reply Qrtly J Econ 77:336–342
Etner J, Jeleva M, Tallon JM (2012) Decision theory under ambiguity. J of Econ Surveys 26(2):234–270
Gardenfors P, Sahlin NE (1982) Unreliable probabilities, risk taking, and decision making Synthese 53:361–386
Ghemawat P (1991) Commitment. Simon and Schuster, New York
Ghirardato P (2001) Coping with ignorance: unforeseen contingencies and non-additive uncertainty. Econ Th 17(2):247–276
Gollier C (2014) Optimal insurance design of ambiguous risks. Econ Theory 57(3):555–576
Hahn T, Preuss L, Pinkse J, Figge F (2014) Cognitive frames in corporate sustainability: Managerial sensemaking with paradoxical and business case frames. Acad Man Rev 39(4):463–487
Hanany E, Klibanoff P, Mukerji S (2020) Incomplete information games with ambiguity averse players. Amer Econ J : Microecon 12(2):135–187
Hertwig R, Pleskac TJ, Pachur T (2019) Taming Uncertainty. MIT Press
Hodgson GM (2011) The eclipse of the uncertainty concept in mainstream economics. J of Econ Issues 45(1):159–176
Holm HJ, Opper S, Nee V (2013) Entrepreneurs under uncertainty: An economic experiment in China. Man Sci 59(7):1671–1687
Kahneman D, Tversky A (1979) Prospect theory: An analysis of decision under risk. Econometrica 47:263–291
Korhonen PJ, Wallenius J (2020) Making Better Decisions. Springer International Publishing
Machina MJ (2014) Ambiguity Aversion with Three or More Outcomes. Amer Econ Rev 104(12):3814–3840
Meyer RJ, Banks D (1997) Behavioral Theory and Naïve Strategic Reasoning. In: Day GS, Reibstein DJ, Gunther RE (eds) Wharton on Dynamic Competitive Strategy. John Wiley & Sons Inc, New York, NY)
Packard MD, Clark BB, Klein PG (2017) Uncertainty types and transitions in the entrepreneurial process. Org Sci 28(5):840–856
Paraschiv C, Shyti A (2016) Entrepreneurs Under Ambiguity: A Prospect Theory Perspective. Das TK, ed. Decision Making in Behavioral Strategy (Information Age Publishing, Charlotte, NC), 25–47
Petkova AP, Wadhwa A, Xin Y, Jain S (2014) Reputation and Decision Making Under Ambiguity: A Study of U.S. Venture Capital Firms’ Investments in the Emerging Clean Energy Sector. Acad Man J 57(2):422–448
Phillips ND, Hertwig R, Kareev Y, Avrahami J (2014) Rivals in the dark: How competition influences search in decisions under uncertainty. Cognition 133(1):104–119
Savage LJ (1954) The Foundations of Statistics. Wiley, New York
Sillince J, Jarzabkowski P, Shaw D (2012) Shaping Strategic Action Through the Rhetorical Construction and Exploitation of Ambiguity. Org Sci 23(3):630–650
Srivastava SB (2015) Intraorganizational Network Dynamics in Times of Ambiguity. Org Sci 26(5):1365–1380
Townsend DM, Hunt RA, McMullen JS, Sarasvathy SD (2018) Uncertainty, knowledge problems, and entrepreneurial action. Acad Man Annals 12(2):659–687
Tversky A, Kahneman D (1992) Advances in prospect theory: Cumulative representation of uncertainty. J Risk and Uncertainty 5(4):297–323
Yates JF, Zukowski LG (1976) Characterization of ambiguity in decision making. Beh Sci 21:19–25
Zadeh LA (1978) Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets & Sys 1:3–28
Funding
This study was not funded.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest/Competing interests
The author (Arend) declares he has no conflicts of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Arend, R.J. Strategic decision-making under ambiguity: insights from exploring a simple linked two-game model. Oper Res Int J 22, 5845–5861 (2022). https://doi.org/10.1007/s12351-022-00728-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12351-022-00728-8