Marginal rates in DEA using defining hyperplanes of PPS with CRS technology

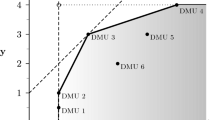
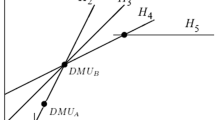
Abstract

Data envelopment analysis (DEA) was proposed in a highly influential paper by Charnes et al. (J Oper Res 2:429–444, 1978), who developed the Farrell seminal research (J R Stat Soc 120:253–290, 1957). The aim of the present research is calculating marginal rates for strong and weak efficient decision making units (DMUs) using the defining hyperplanes of the production possibility set (PPS). Toward this end, there are three essential objectives in the current study: (1) Implement Farrell’s idea to construct a new PPS called the Farrell PPS. In doing so, important relationships were discovered between the PPSs with constant returns to scale (CRS), non-increasing returns to scale, and non-decreasing returns to scale technologies. (2) Apply the newly constructed Farrell PPS as a catalyst to obtain strong and weak efficient DMUs and explicit form equations of strong and weak defining hyperplanes for the PPS with CRS technology. In order to do this task, a multiple objective linear programming problem is proposed whose structure for the decision space of the criterion space is similar to the proposed Farrell PPS. (3) Calculate the marginal rates for strong and weak efficient DMUs using the obtained explicit form equations of strong and weak defining hyperplanes for the PPS with CRS technology. Finally, an empirical study in the Iranian banking sector is used to show the applicability of the proposed methods.

Appendices

Appendix A

1.1 A.1 Original $T_C$ with two inputs and one output and iterations of constructing the Farrell PPS in two cases

See Figs. 5, 6, 7.

Fig. 5

$T_C$ in the three dimensional space with one output and two inputs

Fig. 6

Iterations of cutting $T_C$ using the hyperplane $y=k$

Fig. 7

Iterations of cutting $T_C$ using the hyperplane $x_2=k$

1.2 A.2 Original $T_C$ with one input and two outputs and iterations of constructing the Farrell PPS in two cases

See Figs. 8, 9, 10.

Fig. 8

$T_C$ in the three dimensional space with two outputs and one input

Fig. 9

Iterations of cutting $T_C$ using the hyperplane $y_1=k$

Fig. 10

Iterations of cutting $T_C$ using the hyperplane $x=k$

Appendix B

1.1 B.1 Proof of Theorem 2

Suppose $({x^\prime }^*,{y^\prime }^*,\lambda ^*)$ is a weak efficient solution of MOLP (20). It is proven that $({x^\prime }^*,{y^\prime }^*)$ is a weak or strong efficient unit in $T_F$. By contradiction, suppose $({x^\prime }^*,{y^\prime }^*)$ is not a weak efficient unit in $T_F$, and thus, it will not be strong efficient. Hence, there exists $(\widehat{x^\prime },\widehat{y^\prime })\in T_F$ whereas $(-\widehat{x^\prime },\widehat{y^\prime })>(-{x^\prime }^*,{y^\prime }^*)$. Because $(\widehat{x^\prime },\widehat{y^\prime })\in T_F$, there exists $\widehat{\lambda }\geqslant 0$ where

$$\begin{aligned} \begin{array}{rlll} &&\displaystyle \sum _{j=1}^n\widehat{\lambda }_j\overline{x}^\prime _{ij}\leqslant \widehat{x^\prime }_i,&i=1,\ldots ,m,\\ &&\displaystyle \sum _{j=1}^n\widehat{\lambda }_j\overline{y}^\prime _{rj}\geqslant \widehat{y^\prime }_r,&r=1,\ldots ,s-1,\\ &&\displaystyle \sum _{j=1}^n\widehat{\lambda }_j\geqslant 1. \end{array}\end{aligned}$$

(28)

Constraints (28) imply $(\widehat{x^\prime },\widehat{y^\prime },\widehat{\lambda })$ is a feasible solution of MOLP (20) whereas $(-\widehat{x^\prime },\widehat{y^\prime })>(-{x^\prime }^*,{y^\prime }^*)$, which is a contradiction.

Conversely, suppose $({x^\prime }^*,{y^\prime }^*)$ is a weak or strong efficient unit in $T_F$. It is proven that $({x^\prime }^*,{y^\prime }^*,\lambda ^*)$ is a weak efficient solution of MOLP (20). Because $({x^\prime }^*,{y^\prime }^*)\in T_F$, there exists $\lambda ^*\geqslant 0$ where

$$\begin{aligned} \begin{array}{rlll} &&\displaystyle \sum _{j=1}^n\lambda _j^*\overline{x}^\prime _{ij}\leqslant {x_i^\prime }^*,&i=1,\ldots ,m,\\ &&\displaystyle \sum _{j=1}^n\lambda _j^*\overline{y}^\prime _{rj}\geqslant {y_r^\prime }^*,&r=1,\ldots ,s-1,\\ &&\displaystyle \sum _{j=1}^n\lambda _j^*\geqslant 1.& \end{array}\end{aligned}$$

(29)

Constraints (29) imply $({x^\prime }^*,{y^\prime }^*,\lambda ^*)$ is a feasible solution of MOLP (20). Because $({x^\prime }^*,{y^\prime }^*)$ is a weak or strong efficient unit in $T_F$, there does not exist $(\widehat{x^\prime },\widehat{y^\prime })\in T_F$ whereas $(-\widehat{x^\prime },\widehat{y^\prime })>(-{x^\prime }^*,{y^\prime }^*)$. Hence, $({x^\prime }^*,{y^\prime }^*,\lambda ^*)$ is a weak efficient solution of MOLP (20). $\Box$

1.2 B.2 Proof of Theorem 3

Suppose $({x^\prime }^*,{y^\prime }^*,\lambda ^*)$ is an extreme weak efficient point in the feasible region of the decision space for MOLP (20). It is proven that $({x^\prime }^*,{y^\prime }^*)$ is a weak or strong efficient unit in $T_F$ which associates with $DMU_j$ $(j\in \{1,\ldots ,n\})$ in the original PPS. Theorem 2 implies that we only prove $({x^\prime }^*,{y^\prime }^*)$ is a unit in $T_F$ which associates with $DMU_j$ $(j\in \{1,\ldots ,n\})$ in the original PPS. With respect to Remarks 2 and 3, $({x^\prime }^*,{y^\prime }^*,\lambda ^*=e_j)$ $(j\in \{1,\ldots ,n\})$ is an extreme point in the feasible region of the decision space for MOLP (20) where all constraints of the MOLP problem are satisfied as equality:

$$\begin{aligned} \begin{array}{rlll} &&\displaystyle \sum _{j=1}^ne_j\overline{x}^\prime _{ij}={ x_i^\prime }^*,&i=1,\ldots ,m,\\ &&\displaystyle \sum _{j=1}^ne_j\overline{y}^\prime _{rj}={ y_r^\prime }^*,&r=1,\ldots ,s-1,\\ &&\displaystyle \sum _{j=1}^ne_j= 1. \end{array}\end{aligned}$$

(30)

Thus, constraints (30) imply $({x^\prime }^*,{y^\prime }^*)$ is one of the n units $(\overline{x}^\prime _j,\overline{y}^\prime _j)$ which associates with $DMU_j$ in the original PPS $(j\in \{1,\ldots ,n\})$.

Conversely, suppose $({x^\prime }^*,{y^\prime }^*)$ is a weak or strong efficient unit in $T_F$ which associates with $DMU_j$ $(j\in \{1,\ldots ,n\})$ in the original PPS. It is proven that $({x^\prime }^*,{y^\prime }^*,\lambda ^*)$ is an extreme weak efficient point in the feasible region of the decision space for MOLP (20). Since $({x^\prime }^*,{y^\prime }^*)$ is a unit which corresponds to one of the n DMUs in the original PPS, $\lambda ^*=e_j$ $(j\in \{1,\ldots ,n\})$ is satisfied in MOLP (20). Then, regarding Theorem 2, we only prove $({x^\prime }^*,{y^\prime }^*,\lambda ^*=e_j)$ $(j\in \{1,\ldots ,n\})$ is an extreme point in the feasible region of the decision space for MOLP (20). The definition of an extreme point implies that we must prove in the point $({x^\prime }^*,{y^\prime }^*,\lambda ^*=e_j)$ $(j\in \{1,\ldots ,n\})$, $n+m+s-1$ linearly independent constraints (along with non-negative variables) of the feasible region of the decision space for MOLP (20) are binding. Because $({x^\prime }^*,{y^\prime }^*)$ is associated with one of the n DMUs in the original PPS, without loss of generality, consider $({x^\prime }^*,{y^\prime }^*)=(\overline{x}^\prime _1,\overline{y}^\prime _1)$ i.e. $j=1$. Therefore, constraints of MOLP (20) which are binding in the point $({x^\prime }^*,{y^\prime }^*,\lambda ^*)=(\overline{x}^\prime _1,\overline{y}^\prime _1,e_1)$ are as follows:

$$\begin{aligned} \begin{array}{rlll} &&1\overline{x}^\prime _{11}+0\overline{x}^\prime _{12}+\cdots +0\overline{x}^\prime _{1n}-\overline{x}^\prime _{11}=0,\\ &&\vdots \\ &&1\overline{x}^\prime _{m1}+0\overline{x}^\prime _{m2}+\cdots +0\overline{x}^\prime _{mn}-\overline{x}^\prime _{m1}=0,\\ &&1\overline{y}^\prime _{11}+0\overline{y}^\prime _{12}+\cdots +0\overline{y}^\prime _{1n}-\overline{y}^\prime _{11}=0,\\ &&\vdots \\ &&1\overline{y}^\prime _{(s-1)1}+0\overline{y}^\prime _{(s-1)2}+\cdots +0\overline{y}^\prime _{(s-1)n}-\overline{y}^\prime _{(s-1)1}=0,\\ &&\lambda _1=1,\\ &&\lambda _2=0,\\ &&\vdots \\ &&\lambda _n=0. \end{array}\end{aligned}$$

(31)

On the other hand, (31) implies that all the input and output constraints of MOLP (20) in this point are binding. The coefficients matrix of MOLP (20) corresponding to the equations (31) is as follows:

$$\begin{aligned} \begin{array}{rlll} \Upsilon =\begin{bmatrix} \overline{x}^\prime _{11} & \overline{x}^\prime _{12} & \ldots & \overline{x}^\prime _{1n} && -1 & 0 & \ldots & 0\\ \vdots & \vdots & & \vdots & & 0 & -1 & & 0 \\ \vdots & \vdots & & \vdots & & \vdots & & \ddots & \vdots \\ \overline{y}^\prime _{(s-1)1}& \overline{y}^\prime _{(s-1)2} & \ldots & \overline{y}^\prime _{(s-1)n} & & 0 & \ldots & & -1\\ \\ 1 & 0 & \ldots & 0 & & 0 & \ldots & \ldots & 0\\ 0 & 1 & & 0 & & 0 & \ldots & \ldots & 0 \\ \vdots & & \ddots & \vdots & & 0 & \ldots & \ldots & 0 \\ 0 & \ldots & & 1 & & 0 & \ldots & \ldots & 0 \end{bmatrix} \end{array}\end{aligned}$$

(32)

Matrix $\Upsilon$ is a block diagonal matrix where its determinant is non-zero. It is noted that the rank of $\Upsilon$ is $m+s-1+n$. Therefore, $({x^\prime }^*,{y^\prime }^*,\lambda ^*=e_j)$ $(j\in \{1,\ldots ,n\})$ is an extreme point in the feasible region of the decision space for MOLP (20). $\Box$

1.3 B.3 Proof of Theorem 4

Suppose $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})$ is a unit in $T_F$. It is proven that $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ is a ray in $T_C$. $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})$ belongs to $T_F$, and thus, (15) implies

$$\begin{aligned} \begin{array}{rlll} & & x^\prime _i-\displaystyle \sum _{j=1}^n\lambda _j\frac{\overline{x}_{ij}}{\overline{y}_{sj}}\geqslant 0,& i=1,\ldots ,m,\\ & & \quad -y^\prime _r+\displaystyle \sum _{j=1}^n\lambda _j\frac{\overline{y}_{rj}}{\overline{y}_{sj}}\geqslant 0,& r=1,\ldots ,s-1,\\ & & \quad \displaystyle \sum _{j=1}^n\lambda _j\geqslant 1.& (*) \end{array}\end{aligned}$$

(33)

We can rewrite the constraint $(*)$ in (33) as $-1+\displaystyle \sum\nolimits _{j=1}^n\lambda _j\frac{\overline{y}_{sj}}{\overline{y}_{sj}}\geqslant 0$. Let $k_j=\frac{1}{\overline{y}_{sj}}>0$, then the constraints (33) convert to:

$$\begin{aligned} \begin{array}{rlll} & & x^\prime _i-\displaystyle \sum _{j=1}^n\lambda _j(k_j\overline{x}_{ij})\geqslant 0,& i=1,\ldots ,m,\\ & & \quad -y^\prime _r+\displaystyle \sum _{j=1}^n\lambda _j(k_j\overline{y}_{rj})\geqslant 0,& r=1,\ldots ,s-1,\\ & & \quad -1+\displaystyle \sum _{j=1}^n\lambda _j(k_j\overline{y}_{sj})\geqslant 0.& \end{array}\end{aligned}$$

(34)

By Changing variable $\lambda _j$ instead of $\lambda _jk_j$ $(j=1,\ldots ,n)$, the constraints (34) convert to:

$$\begin{aligned} \begin{array}{rlll} & & x^\prime _i-\displaystyle \sum _{j=1}^n\lambda _j\overline{x}_{ij}\geqslant 0,& i=1,\ldots ,m,\\ & & \quad -y^\prime _r+\displaystyle \sum _{j=1}^n\lambda _j\overline{y}_{rj}\geqslant 0,& r=1,\ldots ,s-1,\\ & & \quad -1+\displaystyle \sum _{j=1}^n\lambda _j\overline{y}_{sj}\geqslant 0.& \end{array}\end{aligned}$$

(35)

Constraints (35) imply $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ belongs to $T_C$. Because $T_C$ is a cone, $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ is a ray. Therefore, for each $\alpha >0$, $\frac{1}{\alpha }(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ belongs to $T_C$. Moreover, if $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})$ is an extreme unit in $T_F$, it is proven that $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ is an extreme ray in $T_C$. By contradiction, suppose $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ is not an extreme ray in $T_C$. Therefore, there exist scalars $\alpha _1,~\alpha _2>0$, and rays $(x^1_1,\ldots ,x^1_m,y^1_1,\ldots ,y^1_{s-1},1)$ and $(x^2_1,\ldots ,x^2_m,y^2_1,\ldots ,y^2_{s-1},1)$ in $T_C$ where

$$\begin{aligned} & (x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)=\alpha _1(x^1_1,\ldots ,x^1_m,y^1_1,\ldots ,y^1_{s-1},1) \\ & \quad + \alpha _2(x^2_1,\ldots ,x^2_m,y^2_1,\ldots ,y^2_{s-1},1). \end{aligned}$$

(36)

Since $\alpha _1,\alpha _2>0$, (36) implies $\alpha _1+\alpha _2=1$, and thus,

$$\begin{aligned} & (x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})=\alpha _1(x^1_1,\ldots ,x^1_m,y^1_1,\ldots ,y^1_{s-1}) \\ & \quad + (1-\alpha _1)(x^2_1,\ldots ,x^2_m,y^2_1,\ldots ,y^2_{s-1}), \end{aligned}$$

(37)

which is a contradiction.

Conversely, suppose $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ is a ray in $T_C$. It is proven that $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})$ is a unit in $T_F$. $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ belongs to $T_C$, and thus, (14) implies

$$\begin{aligned} \begin{array}{rlll} & & x^\prime _i-\displaystyle \sum _{j=1}^n\lambda _j\overline{x}_{ij}^\prime \geqslant 0,& i=1,\ldots ,m,\\ & & \quad -y^\prime _r+\displaystyle \sum _{j=1}^n\lambda _j\overline{y}_{rj}^\prime \geqslant 0,& r=1,\ldots ,s-1,\\ & & \quad -1+\displaystyle \sum _{j=1}^n\lambda _j\geqslant 0.& \end{array}\end{aligned}$$

(38)

Constraints (38) imply $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})$ belong to $T_F$. Moreover, if $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$ is an extreme ray in $T_C$, it is proven that $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})$ is an extreme point in $T_F$. By contradiction, suppose $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})\in T_F$ is not an extreme unit. Therefore, there are $(x^1_1,\ldots ,x^1_m,y^1_1,\ldots ,y^1_{s-1})$ and $(x^2_1,\ldots ,x^2_m,y^2_1,\ldots ,y^2_{s-1})$ belong to $T_F$ and for each $\gamma \in (0,1)$

$$\begin{aligned} & (x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})=\gamma (x^1_1,\ldots ,x^1_m,y^1_1,\ldots ,y^1_{s-1}) \\ & \quad + (1-\gamma )(x^2_1,\ldots ,x^2_m,y^2_1,\ldots ,y^2_{s-1}). \end{aligned}$$

(39)

Since $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1})$, $(x^1_1,\ldots ,x^1_m,y^1_1,\ldots ,y^1_{s-1})$ and $(x^2_1,\ldots ,x^2_m,y^2_1,\ldots ,y^2_{s-1})$ belong to $T_F$, $(x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)$, $(x^1_1,\ldots ,x^1_m,y^1_1,\ldots ,y^1_{s-1},1)$, and $(x^2_1,\ldots ,x^2_m,y^2_1,\ldots ,y^2_{s-1},1)$ belong to $T_C$. Therefore, (39) implies

$$\begin{aligned} & (x^\prime _1,\ldots ,x^\prime _m,y^\prime _1,\ldots ,y^\prime _{s-1},1)=\gamma (x^1_1,\ldots ,x^1_m,y^1_1,\ldots ,y^1_{s-1},1) \\ & \quad + (1-\gamma )(x^2_1,\ldots ,x^2_m,y^2_1,\ldots ,y^2_{s-1},1), \end{aligned}$$

(40)

is established in $T_C$, which is a contradiction. $\Box$

1.4 B.4 Proof of Theorem 6

Suppose S is an affine independent set in $\Re ^{m+s-1}$. It is proven that $\overline{S}$ is an affine independent set in $\Re ^{m+s}$. According to the concept of affine independency, suppose $T=\{(x^\prime _2-x^\prime _1,y^\prime _2-y^\prime _1),\ldots ,(x^\prime _k-x^\prime _1,y^\prime _k-y^\prime _1)\}$ is a linear independent set in $\Re ^{m+s-1}$. We prove $\overline{T}=\{(x^\prime _2-x^\prime _1,y^\prime _2-y^\prime _1,0),\ldots ,(x^\prime _k-x^\prime _1,y^\prime _k-y^\prime _1,0),(-x^\prime _1,-y^\prime _1,-1)\}$ is a linear independent set in $\Re ^{m+s}$. By contradiction, suppose $\overline{T}$ is not a linear independent set in $\Re ^{m+s}$. Therefore, there is a vector $(\alpha _1,\ldots ,\alpha _k)\ne 0$ where

$$\begin{aligned} & \alpha _1(x^\prime _2-x^\prime _1,y^\prime _2-y^\prime _1,0)+\cdots +\alpha _t(x^\prime _{t+1}-x^\prime _1,y^\prime _{t+1}-y^\prime _1,0) \\ & \quad + \cdots +\alpha _{k-1}(x^\prime _k-x^\prime _1,y^\prime _k-y^\prime _1,0)+\alpha _k(-x^\prime _1,-y^\prime _1,-1)=(0,0,0). \end{aligned}$$

(41)

(41) implies $\alpha _k=0$, so there is at least one index $t(\ne k)$ where $\alpha _t\ne 0$. Consequently, there exists $\alpha _t\ne 0$ where

$$\begin{aligned} & \alpha _1(x^\prime _2-x^\prime _1,y^\prime _2-y^\prime _1)+\cdots +\alpha _t(x^\prime _{t+1}-x^\prime _1,y^\prime _{t+1}-y^\prime _1) \\ & \quad + \cdots +\alpha _{k-1}(x^\prime _k-x^\prime _1,y^\prime _k-y^\prime _1)=(0,0), \end{aligned}$$

(42)

which is a contradiction.

Conversely, suppose $\overline{S}$ is an affine independent set in $\Re ^{m+s}$. It is proven that S is an affine independent set in $\Re ^{m+s-1}$. Likewise, suppose $\overline{T}$ is a linear independent set in $\Re ^{m+s}$. We prove T is a linear independent set in $\Re ^{m+s-1}$. By contradiction, suppose T is not a linear independent set in $\Re ^{m+s-1}$. Therefore, there is a vector $(\alpha _1,\ldots ,\alpha _{k-1})\ne 0$ where (42) is established. Moreover, (42) implies

$$\begin{aligned} & \alpha _1(x^\prime _2-x^\prime _1,y^\prime _2-y^\prime _1,0)+\cdots +\alpha _t(x^\prime _{t+1}-x^\prime _1,y^\prime _{t+1}-y^\prime _1,0) \\ & \quad + \cdots +\alpha _{k-1}(x^\prime _k-x^\prime _1,y^\prime _k-y^\prime _1,0)+0=(0,0,0). \end{aligned}$$

(43)

Assume $0=\alpha _k$, and thus, (43) implies (41). On the other hand, $(\alpha _1,\ldots ,\alpha _{k-1})\ne 0$ implies $(\alpha _1,\ldots ,\alpha _{k-1},0)\ne 0$, and thus, $\overline{T}$ is not a linear independent set, which is a contradiction. $\Box$

1.5 B.5 Proof of Theorem 7

Each point $(x,y,\lambda )=(\widehat{x},\widehat{y},\widehat{\lambda })$ which satisfies in the following constraints,

$$\begin{aligned} \begin{array}{rlll} & & \displaystyle \sum _{j=1}^n \lambda _j\overline{x}_{ij}\leqslant x_i,& i=1,\ldots ,m,\\ & & \displaystyle \sum _{j=1}^n \lambda _j\overline{y}_{rj}\geqslant y_r,& r=1,\ldots ,s,\\ & & \lambda _j\geqslant 0,& j=1,\ldots ,n,\\ & & x_i \geqslant 0,~y_r\geqslant 0,& i=1,\ldots ,m,~r=1,\ldots ,s, \end{array}\end{aligned}$$

(44)

results in

$$\begin{aligned} \begin{array}{rlll} & & \displaystyle \sum _{j=1}^n \omega \widehat{\lambda }_j\overline{x}_{ij}\leqslant \omega \widehat{x}_i,& i=1,\ldots ,m,\\ & & \displaystyle \sum _{j=1}^n \omega \widehat{\lambda }_j\overline{y}_{rj}\geqslant \omega \widehat{y}_r,& r=1,\ldots ,s,\\ & & \omega \widehat{\lambda }_j\geqslant 0,& j=1,\ldots ,n,\\ & & \omega \widehat{x}_i \geqslant 0,~\omega \widehat{y}_r\geqslant 0,& i=1,\ldots ,m,~r=1,\ldots ,s, \end{array}\end{aligned}$$

(45)

where $\omega \geqslant 0$, i.e., $(\omega \widehat{x},\omega \widehat{y},\omega \widehat{\lambda })$ belongs to the constraints (44). Therefore, the feasible region of the decision space for an MOLP problem by the constraints (44) is a cone. This cone includes the origin because $(x,y,\lambda )=(0,0,0) \in \Re ^{m+s+n}$ satisfies in (44). The feasible region of the decision space belongs to Quadrant I (all points in this quadrant have non-negative coordinates) and the origin is its extreme point because it lies on the $m+s+n$ linearly independent hyperplanes, including $x_i=0$ $(i=1,\ldots ,m)$, $y_r=0$ $(r=1,\ldots ,s)$, and $\lambda _j=0$ $(j=1,\ldots ,n)$. Since each cone has at last one extreme point, the origin is the only extreme point in the feasible region of the decision space formed by the constraints (44). $\Box$

Appendix C

Let $k^\prime$ and $l^\prime$ be respectively the number of extreme points and extreme directions (if any) in the feasible region of the decision space for MOLP (20). Then, regarding the representation theorem (Bazaraa et al. 2010, p. 77), each point $(x^\prime ,y^\prime ,\lambda )$ in the feasible region of the decision space can be represented as follows:

$$\begin{aligned} \begin{array}{rll} & & (x^\prime ,y^\prime ,\lambda )=\displaystyle \sum _{\jmath =1}^{k^\prime }\alpha _{\jmath } (\overline{x}^\prime _{\jmath },\overline{y}^\prime _{\jmath },e_{\jmath })+ \displaystyle \sum _{\imath =1}^{l^\prime }\beta _{\imath } (d^{x^\prime }_{\imath },d^{y^\prime }_{\imath },d^\lambda _{\imath }),\\ & & 1=\displaystyle \sum _{\jmath =1}^{k^\prime }\alpha _{\jmath },\\ & & \alpha _{\jmath }\geqslant 0,~~\beta _{\imath }\geqslant 0,~~\jmath =1,\ldots ,k^\prime ,~\imath =1,\ldots ,l^\prime , \end{array}\end{aligned}$$

(46)

where $(\overline{x}^\prime _{\jmath },\overline{y}^\prime _{\jmath },e_{\jmath })$ $( \jmath =1,\ldots ,k^\prime )$ and $(d^{x^\prime }_{\imath },d^{y^\prime }_{\imath },d^\lambda _{\imath })$ $(\imath =1,\ldots ,l^\prime )$ are respectively extreme points and extreme directions in the feasible region of the decision space for MOLP (20). Regarding the relation between the feasible region of the decision space for MOLP (20) and the PPS, the constraints (46) convert to:

$$\begin{aligned} \begin{array}{rll} & & (x^\prime ,y^\prime )=\displaystyle \sum _{\jmath =1}^{k^\prime }\alpha _{\jmath } (\overline{x}^\prime _{\jmath },\overline{y}^\prime _{\jmath })+ \displaystyle \sum _{\imath =1}^{l^\prime }\beta _{\imath } (d^{x^\prime }_{\imath },d^{y^\prime }_{\imath }),\\ & & 1=\displaystyle \sum _{\jmath =1}^{k^\prime }\alpha _{\jmath },\\ & & \alpha _{\jmath }\geqslant 0,~~\beta _{\imath }\geqslant 0,~~\jmath =1,\ldots ,k^\prime ,~\imath =1,\ldots ,l^\prime . \end{array}\end{aligned}$$

(47)

It is worth mentioning that $(\overline{x}^\prime _{\jmath },\overline{y}^\prime _{\jmath }) \in \Re ^{m+s-1}$ and $(d^{x^\prime }_{\imath },d^{y^\prime }_{\imath })\in \Re ^{m+s-1}$ may not be the extreme unit and the extreme direction in $T_F$.

In PPSs like $T_F$ there is no face which is not strict subset of a facet. Therefore, the proposed method in Sect. 3.2 determines all strong and weak efficient units and directions which lie on same strong and weak efficient facets. By developing these facets, strong (if any) and weak defining hyperplanes of the PPS on the basis of the constraints (47) are specified as follows:

$$\begin{aligned} \begin{array}{rll} H=\{(x^\prime ,y^\prime ) |(x^\prime ,y^\prime )=\displaystyle \sum _{\jmath =1}^{k^{\prime \prime }}\alpha _{\jmath } (\overline{x}^\prime _{\jmath },\overline{y}^\prime _{\jmath })+ \displaystyle \sum _{\imath =1}^{l^{\prime \prime }}\beta _{\imath } (d^{x^\prime }_{\imath },d^{y^\prime }_{\imath }),~~ 1=\displaystyle \sum _{\jmath =1}^{k^{\prime \prime }}\alpha _{\jmath }\}, \end{array}\end{aligned}$$

(48)

where $k^{\prime \prime }\leqslant k^{\prime }$ and $l^{\prime \prime }\leqslant l^{\prime }$, and also $\alpha _{\jmath }$, $\beta _{\imath }\in \Re$ $(\jmath =1,\ldots ,k^{\prime \prime }$, $\imath =1,\ldots ,l^{\prime \prime })$. In fact, H in (48) obtains a defining hyperplane of the PPS which passes on the specified $k^{\prime \prime }$ units and $l^{\prime \prime }$ directions that are on the same weak or strong efficient facet. Since $T_F$ is constructed in the $m+s-1$ dimensional space, $(k^{\prime \prime }+l^{\prime \prime })\geqslant (m+s-1)$. Therefore, arbitrarily select $m+s-1$ units and directions which belong to the same facet. Indeed, $k^{\prime \prime }+l^{\prime \prime }-m-s+1$ columns in (48) are redundant (if any). The parameter matrix for the constraints (48) is,

$$\begin{aligned} \begin{array}{rll} \Phi =\begin{bmatrix} x^\prime & \overline{x}^\prime _{\jmath } & d^{x^\prime }_{\imath } \\ y^\prime & \overline{y}^\prime _{\jmath } & d^{y^\prime }_{\imath } \\ 1 & 1 & 0 \end{bmatrix}. \end{array}\end{aligned}$$

(49)

The dimension for the matrix $\Phi$ is $(m+s)\times (m+s)$. That is, the number of columns belonging to all indexes of $\jmath$ and $\imath$ is $m+s-1$. The determinate of the matrix $\Phi$ obtains an explicit form equation of defining hyperplane which pass on units and directions (if any) which lie on the same facet in $T_F$. This method is applicable and holds to obtain explicit form equations of hyperplanes in high dimensions.

Appendix D

Numerical Example:

Consider a system of five DMUs, each consuming two inputs to produce one output. Table 6 lists the data.

Table 6 The data for the numerical example

Given the data in Table 6, the MOLP problem in the direct method leads to:

$$\begin{aligned} \begin{array}{rlll} & { Max}& \{-x_1,-x_2,y\}\\ & { s}.{ t}.& -2\lambda _1-9\lambda _2-5\lambda _3-8\lambda _4-24\lambda _5+x_1-s_1^-=0,\\ & & -10\lambda _1-9\lambda _2-2\lambda _3-8\lambda _4-12\lambda _5+x_2-s_2^-=0,\\ & & -2\lambda _1-3\lambda _2-\lambda _3-2\lambda _4-4\lambda _5+y+s^+=0,\\ & & \lambda _{j}\geqslant 0,~~~~~~j=1,\ldots ,5,\\ & & s_1^-\geqslant 0,~s_2^-\geqslant 0,~s^+\geqslant 0,\\ & & x_1\geqslant 0,~x_2\geqslant 0,~y\geqslant 0. \end{array}\end{aligned}$$

(50)

To obtain an initial weak efficient BFS for MOLP (50), the linear weighted-sum problem corresponding to this MOLP problem is constructed by considering a non-negative weighting vector, e.g. $\vartheta =(1,1,0)$,

$$\begin{aligned} \begin{array}{rlll} & { Max}& -x_1-x_2\\ & { s}.{ t}.& -2\lambda _1-9\lambda _2-5\lambda _3-8\lambda _4-24\lambda _5+x_1-s_1^-=0,\\ & & -10\lambda _1-9\lambda _2-2\lambda _3-8\lambda _4-12\lambda _5+x_2-s_2^-=0,\\ & & -2\lambda _1-3\lambda _2-\lambda _3-2\lambda _4-4\lambda _5+y+s^+=0,\\ & & \lambda _{j}\geqslant 0,~~~~~~j=1,\ldots ,5,\\ & & s_1^-\geqslant 0,~s_2^-\geqslant 0,~s^+\geqslant 0,\\ & & x_1\geqslant 0,~x_2\geqslant 0,~y\geqslant 0. \end{array}\end{aligned}$$

(51)

The problem (51) is solved by the simplex method. The optimal simplex table is as follows (Table 7):

Table 7 The optimal simplex table for the problem (51)

Then, using preliminary pivoting, the initial weak efficient multicriteria simplex table in the basic form is constructed (Murty 1983, p. 116), as shown in Table 8.

Table 8 The initial weak efficient multicriteria simplex table for MOLP (50)

The initial weak efficient BFS is $\chi ^0=(0,0,\ldots ,0) \in \Re ^{11}$ with the objective value $Z(\chi ^0)=(0,0,0) \in \Re ^3$, which corresponds to the origin in $T_C$. It is obvious that with each nonbasic variable entering the basis, $\chi ^0$ is obtained, which is degenerate.

Consider $\{ 1,2,\ldots ,11 \}$ as the index set of variables $\lambda _1$, $\ldots$, $\lambda _5$, $x_1$, $x_2$, y, $s_1^-$, $s_2^-$, and $s^+$. By applying the Isermann subproblem (4) for Table 8, the maximal index sets are $\{1,2\}$, $\{2,3\}$, $\{1,10\}$, and $\{3,9\}$. Therefore, the explicit form equations of the defining hyperplanes for $T_C$ are as follows:

$$\begin{aligned} \begin{array}{rlll} & & H_1=\{(x_1,x_2,y)\mid 6y-x_1-x_2=0\},\\ & & H_2=\{(x_1,x_2,y)\mid 9y-x_1-2x_2=0\},\\ & & H_3=\{(x_1,x_2,y)\mid y-x_1=0\},\\ & & H_4=\{(x_1,x_2,y)\mid 2y-x_2=0\}. \end{array}\end{aligned}$$

(52)