Optimal strategies of social commerce platforms in the context of forwarding and bargaining

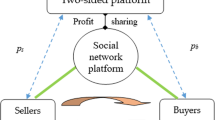
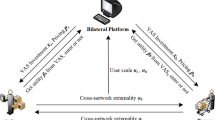
Abstract

“Forwarding and bargaining” is a new marketing pattern in social commerce that fully utilizes consumers’ social relationships and offers an alternative for enterprises struggling with traditional e-commerce platforms. In this paper, we assume a Stackelberg game model between a social commerce platform and an e-commerce enterprise to investigate their strategy changes in four scenarios under the forwarding and bargaining context. Our results show that (1) platforms in the early-mid stage tend to adopt a subsidy strategy to obtain massive user and traffic benefits; (2) for enterprises operating high-quality but low-added-value products, it is unnecessary to join a developed social commerce platform; (3) platforms as direct beneficiaries can always gain more profits than can enterprises from increased traffic benefits; and (4) platforms desire to reduce the forwarding cost, whereas enterprises favour maintaining a higher one.

Appendix

1. Stackelberg stage-one solution

(1) When $dm\ge 1-\frac{n}{N}$, the decision model of the enterprise is

$$\left\{ {\begin{array}{*{20}l} {p^{*} ,m^{*} = {\text{argmax}}_{p,m} Nd\left( {p - c - s} \right)} \hfill \\ {{\text{s.t.}}\,\,dm \ge 1 - \frac{n}{N},0 \le d \le 1,m \ge 0} \hfill \\ \end{array} } \right..$$

Then, we can compute the partial derivatives of $q$ and $m$ as

$$\left\{ {\begin{array}{*{20}l} {\frac{{\partial R_{M} }}{\partial p} = \frac{N}{q}\left( {q + c + s - mt - 2p} \right)} \hfill \\ {\frac{{\partial R_{M} }}{\partial m} = - \frac{{Nt\left( {p - c - s} \right)}}{q} < 0} \hfill \\ \end{array} } \right..$$

Therefore, the optimal solution is at $dm=1-\frac{n}{N}$; thus, we obtain

$$\left\{ {\begin{array}{*{20}l} {p^{*} = \frac{q + c + s}{2} - \frac{{2qt\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill \\ {m^{*} = \frac{{2q\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill \\ {R_{M}^{*} = \frac{{N(q - c - s)^{2} }}{4q} - \left( {N - n} \right)t} \hfill \\ \end{array} } \right..$$

(2) When $dm<1-\frac{n}{N}$, the decision model is

$$\left\{ {\begin{array}{*{20}l} {p^{*} ,m^{*} = {\text{argmax}}_{p,m} \frac{n}{1 - dm}d\left( {p - c - s} \right)} \hfill \\ {{\text{s.t.}}\,\,dm < 1 - \frac{n}{N},0 \le d \le 1,m \ge 0} \hfill \\ \end{array} } \right..$$

Let $\frac{\partial {R}_{M}}{\partial p}=0$ and $\frac{\partial {R}_{M}}{\partial m}=0$; we then have

$$\left\{ {\begin{array}{*{20}l} {p = q - mt - \sqrt {qt} } \hfill \\ {p = \frac{q + c + s}{2} - mt} \hfill \\ \end{array} } \right..$$

These equations have no solution. Therefore, the optimal solution is at $m = 0$, and we can obtain

$$\left\{ {\begin{array}{*{20}l} {p^{*} = \frac{q + c + s}{2}} \\ {m^{*} = 0} \\ {R_{M}^{*} = \frac{{n(q - c - s)^{2} }}{4q}} \\ \end{array} } \right..$$

In summary, the optimal strategy of the enterprise is as follows.

$$\left\{ {\begin{array}{*{20}l} {m^{*} = 0,p^{*} = \frac{q + c + s}{2}} \hfill & {(q - c - s)^{2} < 4qt} \hfill \\ {m^{*} = \frac{{2q\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}},p^{*} = \frac{q + c + s}{2} - \frac{{2qt\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill & {(q - c - s)^{2} \ge 4qt} \hfill \\ \end{array} } \right.$$

2. Stackelberg stage-two solution

We plug the enterprise’s optimal strategy into Eq. (5), and we can obtain the decision model of the platform as

$$\left\{ {\begin{array}{*{20}l} {s^{*} = {\text{argmax}}_{s} R_{W} \left( s \right)} \hfill \\ {{\text{ s}}{\text{.t}}{.}\,\,s + v \ge 0,0 \le d \le 1} \hfill \\ \end{array} } \right.$$

where

$$R_{W} \left( s \right) = \left\{ {\begin{array}{*{20}l} {n\frac{q - c - s}{{2q}}\left( {s + v} \right),} \hfill & {(q - c - s)^{2} < 4qt} \hfill \\ {N\frac{q - c - s}{{2q}}\left( {s + v} \right),} \hfill & {(q - c - s)^{2} \ge 4qt} \hfill \\ \end{array} } \right..$$

KKT conditions can be utilized to find a closed-form solution for this optimization task. The Lagrange dual function can be written as $L(s,{\lambda }_{1},{\lambda }_{2},{\lambda }_{3})=-{R}_{W}(s)+{\lambda }_{1}(-s-v)+{\lambda }_{2}(d-1)+{\lambda }_{3}(-d)$, where ${\lambda }_{\mathrm{1,2},3}\ge 0$. By obtaining the partial derivatives of the Lagrange dual function, the KKT conditions are utilized, and the optimal task assignment coefficients should satisfy the following conditions:

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial L}{{\partial s}} = 0} \hfill \\ {\frac{\partial L}{{\partial \lambda_{i} }} = 0,\quad i = 1,2,3} \hfill \\ {\lambda_{i} \ge 0,\quad i = 1,2,3} \hfill \\ \end{array} } \right..$$

Based on these conditions, the optimal solution to this problem can be divided into the following four scenarios, and each scenario contains proof of the corresponding proposition.

(1) Scenario 1 (Proof of Proposition 1)

When$\left\{\begin{array}{l}\frac{\partial {R}_{W}}{\partial s}<0\\ (q-c-s{)}^{2}\ge 4qt\\ d=1\end{array}\right.$, the KKT conditions are satisfied. Therefore, the optimal solution for the platform is ${s}^{*}=-q-c$ if $v>3q+c$ holds. We plug this solution into $\left\{ {\begin{array}{*{20}l} {p^{*} = \frac{q + c + s}{2} - \frac{{2qt\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill \\ {m^{*} = \frac{{2q\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill \\ {D^{*} = N\frac{q - c - s}{{2q}}} \hfill \\ {R_{M}^{*} = D^{*} \left( {p - s - c} \right)} \hfill \\ {R_{W}^{*} = D^{*} \left( {s + v} \right)} \hfill \\ \end{array} } \right.$ and obtain $\left\{ {\begin{array}{*{20}l} { p^{*} = - \frac{N - n}{N}t} \hfill \\ {m^{*} = \frac{N - n}{N}} \hfill \\ {D^{*} = N} \hfill \\ {R_{M}^{*} = Nq - \left( {N - n} \right)t} \hfill \\ {R_{W}^{*} = N\left( {v - q - c} \right)} \hfill \\ \end{array} } \right.$ immediately.

(2) Scenario 2 (Proof of Proposition 2)

When $\left\{ {\begin{array}{*{20}l} {\frac{{\partial R_{W} }}{\partial s} = 0} \hfill \\ {(q - c - s)^{2} \ge 4qt} \hfill \\ {0 \le d \le 1} \hfill \\ \end{array} } \right.$, the KKT conditions are satisfied. Therefore, the optimal solution for the platform is ${s}^{*}=\frac{q-c-v}{2}$ if $v\le 3q+c\text{ and }t\le \frac{(q-c+v{)}^{2}}{16q}$ hold. We plug this solution into $\left\{ {\begin{array}{*{20}l} {p^{*} = \frac{q + c + s}{2} - \frac{{2qt\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill \\ {m^{*} = \frac{{2q\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill \\ {D^{*} = N\frac{q - c - s}{{2q}}} \hfill \\ {R_{M}^{*} = D^{*} \left( {p - s - c} \right)} \hfill \\ {R_{W}^{*} = D^{*} \left( {s + v} \right)} \hfill \\ \end{array} } \right.$ and obtain $\left\{ {\begin{array}{*{20}l} { p^{*} = \frac{3q + c - v}{4} - \frac{{4\left( {N - n} \right)qt}}{{N\left( {q - c + v} \right)}}} \hfill \\ {m^{*} = \frac{{4\left( {N - n} \right)q}}{{N\left( {q - c + v} \right)}}} \hfill \\ {D^{*} = \frac{q - c + v}{{4q}}N} \hfill \\ {R_{M}^{*} = \frac{{N\left( {q - c + v} \right)^{2} }}{16q} - \left( {N - n} \right)t} \hfill \\ {R_{W}^{*} = \frac{{N\left( {q - c + v} \right)^{2} }}{8q}} \hfill \\ \end{array} } \right.$ immediately.

(3) Scenario 3 (Proof of Proposition 3)

When $\left\{ {\begin{array}{*{20}l} {\frac{{\partial R_{W} }}{\partial s} > 0} \hfill \\ {(q - c - s)^{2} = 4qt} \hfill \\ {0 \le d \le 1} \hfill \\ {R_{W} \ge \left. {R_{W}^{*} } \right|_{{(q - c - s)^{2} < 4qt}} } \hfill \\ \end{array} } \right.$, the KKT conditions are satisfied. Therefore, the optimal solution for the platform is ${s}^{*}=q-c-2\sqrt{qt}$ if $v\le 3q+c, \, t>\frac{(q-c+v{)}^{2}}{16q}\text{ and }n\le \frac{8\sqrt{qt}\left(q-c+v\right)-16qt}{(q-c+v{)}^{2}}N$ hold. We plug this solution into $\left\{ {\begin{array}{*{20}l} {p^{*} = \frac{q + c + s}{2} - \frac{{2qt\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill \\ {m^{*} = \frac{{2q\left( {N - n} \right)}}{{N\left( {q - c - s} \right)}}} \hfill \\ {D^{*} = N\frac{q - c - s}{{2q}}} \hfill \\ {R_{M}^{*} = D^{*} \left( {p - s - c} \right)} \hfill \\ {R_{W}^{*} = D^{*} \left( {s + v} \right)} \hfill \\ \end{array} } \right.$ and obtain $\left\{ {\begin{array}{*{20}l} { p^{*} = q - \frac{2N - n}{N}\sqrt {qt} } \hfill \\ {m^{*} = \frac{N - n}{N}\sqrt{\frac{q}{t}} } \hfill \\ {D^{*} = N\sqrt{\frac{t}{q}} } \hfill \\ {R_{M}^{*} = nt} \hfill \\ {R_{W}^{*} = N\sqrt{\frac{t}{q}} \left( {q - c - 2\sqrt {qt} + v} \right)} \hfill \\ \end{array} } \right.$ immediately.

(4) Scenario 4 (Proof of Proposition 4)

When $\left\{ {\begin{array}{*{20}l} {\frac{{\partial R_{W} }}{\partial s} = 0} \hfill \\ {(q - c - s)^{2} < 4qt} \hfill \\ {0 \le d \le 1} \hfill \\ {R_{W} > \left. {R_{W} } \right|_{{(q - c - s)^{2} = 4qt}} } \hfill \\ \end{array} } \right.$, the KKT conditions are satisfied. Therefore, the optimal solution for the platform is ${s}^{*}=\frac{q-c-v}{2}$ if $v\le 3q+c, \, t>\frac{(q-c+v{)}^{2}}{16q}\text{ and }n>\frac{8\sqrt{qt}\left(q-c+v\right)-16qt}{(q-c+v{)}^{2}}N$ hold. We plug this solution into $\left\{ {\begin{array}{*{20}l} {p^{*} = \frac{q + c + s}{2}} \hfill \\ {m^{*} = 0} \hfill \\ {D^{*} = n\frac{q - c - s}{{2q}}} \hfill \\ {R_{M}^{*} = D^{*} \left( {p - s - c} \right)} \hfill \\ {R_{W}^{*} = D^{*} \left( {s + v} \right)} \hfill \\ \end{array} } \right.$ and obtain $\left\{ {\begin{array}{*{20}l} { p^{*} = \frac{3q + c - v}{4}} \hfill \\ {m^{*} = 0} \hfill \\ {D^{*} = \frac{q - c + v}{{4q}}n} \hfill \\ {R_{M}^{*} = \frac{{n\left( {q - c + v} \right)^{2} }}{16q}} \hfill \\ {R_{W}^{*} = \frac{{n\left( {q - c + v} \right)^{2} }}{8q}} \hfill \\ \end{array} } \right.$ immediately.