Pareto-optimal workforce scheduling with worker skills and preferences

Abstract

This paper addresses employee scheduling in service operations, considering various skill and skill levels and the fluctuating customer demand throughout the day and week. Employee shift and day-off preferences are also considered to enhance morale. We propose a two-stage integer programming model. In the first stage, the model optimizes the number of employees required for each shift period, ensuring uniform distribution of overstaffing to improve customer service. A Pareto frontier approach is applied between the two stages, offering decision-makers a set of non-dominated solutions that balance overstaffing and understaffing. The second stage uses the selected Pareto-optimal solution to assign shifts and day-offs to employees, incorporating their skills, preferences, and fairness considerations. Our model implicitly includes shifts and breaks, reducing decision variables and computational time. Using real data from a dining restaurant chain, we validate the model’s effectiveness in enhancing customer service and reducing labor costs by 12.3% compared to manual scheduling. Furthermore, productivity and employee satisfaction improve by considering individual skills and preferences.

1 Introduction

Workforce scheduling is an intricate problem, especially in service operations where demand fluctuates, and employees possess varying skills and levels. This problem has attracted significant interest from both practitioners and researchers. Managers strive to minimize labor costs through more effective labor schedules that reduce overstaffing. Besides, in the service industry, customers are demanding and impatient, making high-quality customer service reliant on assigning the right number of employees with the appropriate skill sets to the right tasks at the right times (Mirrazavi and Beringer 2007). Furthermore, considering employee preferences and balancing workloads can enhance overall productivity. However, the problem becomes NP-hard when multiple factors, such as employee preferences, availability, and skills are simultaneously considered (Brucker et al. 2011).

Typically, managers are responsible for handling these complex and labor-intensive scheduling duties, making trade-offs between conflicting objectives, such as minimizing labor costs, and maximizing service quality while navigating operational uncertainties. This is where operations research (OR) tools prove invaluable. OR tools provide systematic and quantitative approaches to tackle these challenges, offering managers alternative solutions to streamline the scheduling process. Numerous heuristics, metaheuristics, artificial intelligence, mathematical approaches and decision support systems have been proposed in the literature to reduce the burden and time spent on scheduling (Ozder et al. 2020).

This paper explores the challenges of tour scheduling—which integrates shift and day-off planning—in service industries where customer demand fluctuates hourly throughout the day and across the week. To meet this fluctuating demand and customer expectations, it is crucial to have appropriate number of employees with the required skill sets and levels at the right time. Unlike manufacturing facilities, service facilities do not have standard shifts and day-offs. Since service runs every day of the week throughout the year, it is vital to balance the employees' preferences for day-offs, rest hours, vacations, and work shifts to avoid exhaustion and dissatisfaction thereby maintaining service quality, productivity, and employee morale (Rong 2010).

Thompson (1998a, 1998b) outlines four steps for effective scheduling: (i) Forecasting demand. (ii) Determining labor requirements based on this forecast. (iii) Developing a work schedule that considers employees' requests. (iv) Making minor arrangements as needed based on actual demand.

In our study, we forecast customer demand by analyzing point of sale (POS) data alongside method and time study data to accurately determine the necessary labor requirements. We then use this information in a compact two-stage integer programming model. In the first stage, the model optimizes required employee numbers throughout the day and the week, balancing the workload. A Pareto frontier approach is applied between the two stages, offering decision-makers a set of non-dominated solutions that balance overstaffing and understaffing. After selecting a nondominated solution, in the second stage, the model fairly assigns tasks and shifts based on employee skills, skill levels, and preferences. While we tested our model in a branch of a casual dining restaurant chain, it is applicable to various service organizations, including hotels, retail stores, call centers, and hospitals, especially those with variable demand, overlapping shifts, and labor-intensive work.

To address labor requirement fluctuations, we employ flexible scheduling with varied shift start times and break placements. Lunch and relief breaks, along with their placements, are modeled implicitly. As a result, the proposed model requires substantially fewer variables than the equivalent set covering model for tour scheduling problems with multiple breaks and break windows. Finally, we present a Pareto frontier to assist managers in balancing overstaffing and understaffing costs while maintaining threshold service levels.

The contributions of this article are multi-fold:

• 1. We present a compact integer programming formulation for optimal staffing, including break placements and create a robust schedule by uniformly distributing the overstaffing across the work hours.

• 2. We offer alternative Pareto optimal solutions for managers, balancing service level and labor cost.

• 3. In employee shift scheduling, we incorporate labor skills and fairness through employee day-off and shift start preferences prioritizing higher skill levels.

• 4. We validate our model using actual data from a restaurant chain, showcasing improvements in customer service, productivity, and costs.

The rest of the paper is organized as follows: Sect. 2 reviewed related literature. Section 3 introduces the two-stage model for the general tour scheduling problem and explains the Pareto frontier approach. Section 4 presents the case study and discusses the experimental results of the model. Finally, Sect. 5 concludes the study and proposes directions for future research.

2 Literature review

The workforce scheduling problem was first studied by Edie (1954) and Dantzig (1954), who focused on determining the number of on-duty toll booths while minimizing traffic delays and collector wages. Since then, an extensive body of literature has explored labor scheduling across various application areas, including manufacturing facilities, hospitals, universities, call centers, police stations, airports, and airlines. Van den Bergh et al. (2013) and Ozder et al. (2020) provide an extensive review of labor scheduling.

Several frameworks have been developed for general employee scheduling problems (Glover and McMillan 1986; Eveborn and Rönnqvist 2004; Sauer and Schumann 2007; and Kletzander and Musliu 2020). These frameworks are versatile and can be applied across various fields. Conversely, many studies focus on specific application areas, each with unique characteristics, requirements, and constraints.

De Bruecker et al. (2015) provide a comprehensive literature review on workforce scheduling that incorporates skills, guiding researchers towards developing more realistic models. Besides, Loucks (2018) surveys labor scheduling models in service operations and finds that only 15% of the articles address employee preferences, though there is an increasing trend in models considering preferences, especially in healthcare, where 60% of the surveyed models are applied to hospital nurses.

One key consideration in specific area studies is the inclusion of worker preferences. For example, Topaloglu (2009) addressed scheduling hospital physicians’ shifts and days off, considering preferences and seniority. Rong (2010) focused on tour scheduling for a service organization managing live plants, respecting employees’ weekend-off preferences. Özgüven and Sungur (2013) investigated hierarchical labor scheduling where higher-qualified workers can substitute for lower-qualified ones. Various other studies (Akbari et al. 2013; Shuib and Kamarudin 2019; Rijal et al. 2021) have explored different aspects of scheduling preferences in healthcare and other sectors.

Additionally, fairness is another crucial factor, such as balancing workloads or satisfying employee preferences based on various criteria. This includes implementing a look-back scheduling policy that prioritizes workers whose preferences were not adequately met in previous schedules. While some use a one-month or longer planning horizon (e.g., Rong 2010; Cheng and Kuo 2016; Ağrali et al., 2017), others update the fairness score weekly to maintain equity (e.g., Topaloglu 2009).

Workforce scheduling is inherently multi-objective, involving conflicting goals. Many studies aggregate criteria into a single objective function, though the use of Pareto-optimality is rare. Lin et al. (2012) generated Pareto-optimal schedules, which reduce the nurses' fatigue with a slight decrement in their preferences. Burke et al. (2012) used the concept to handle several soft constraints of a multi-objective nurse scheduling problem. Schulte et al. (2017) used bilevel optimization for long-term scheduling in call centers, determining staffing qualifications at the upper level and the number of workers at the lower level. By using the Pareto-set of the lower-level problem, they made relevant staffing decisions while avoiding long computation times in the upper stage. Taghizadehalvandi and Kamisli (2019) utilized Pareto optimality to balance the total workloads and the preferences of a technology store employees.

In mathematical models, shifts are modeled either implicitly or explicitly. Explicit modeling, as done by Dantzig (1954) becomes intractable as problem size and complexity increase. Models with implicit shift formulations reduce the number of variables. Aykin (1996) used implicit break times in specified windows, reducing variables with additional constraints. Brusco and Jacobs (2000) developed an implicit integer programming formulation for meal-break windows, start-time bands, and intervals to enhance productivity and flexibility. Sungur et al. (2017) addressed multiple breaks with varying durations and windows to ensure ideal break periods and balanced working times. Álvarez et al. (2020) introduced a methodology for assigning shifts with multiple breaks, providing necessary flexibility to reduce staff surpluses and shortages.

Despite extensive research in workforce scheduling, the hospitality industry has not been thoroughly examined (Rocha et al. 2012). The complexity of scheduling in this sector is due to the numerous daily shifts (Loucks 2018). Some studies, mainly focused on fast-food restaurants, have proposed models to optimize staffing (Curin et al. 2005; Zouhar and Havlová, 2012; Liggayu et al. 2018; Noor et al. 2022; Nasir et al. 2022; Ahamad and Ghani 2023). However, few studies have considered dining restaurants, which have unique scheduling challenges (Van den Bergh et al. 2013).

This research gap is significant because dining restaurants often involve more diverse roles, varying skill sets, and potentially more complex customer interactions compared to fast-food environments. For instance, Choi et al. (2009) examine the balancing of full-time and part-time workers in a restaurant to maintain service levels and reduce labor costs, but do not consider the specific skills required for each role or how individual preferences might be incorporated into the scheduling process. Akhundov et al. (2022) create a scheduling model for waitstaff that considers experience levels, preferences, and availability to ensure a fair workload distribution. However, their model does not account for the specific skills required for different roles within the restaurant. Similarly, Inan (2023) develops a model that schedules waiters and bussers with a fair workload. Nonetheless, this model does not incorporate individual employee preferences or the varying skill levels needed for different tasks, which are crucial for maintaining high service quality and employee satisfaction.

Table 1 provides a comprehensive comparison of workforce scheduling models in literature, highlighting key features. The comparison reveals significant variation in how models address these features across different industries, including healthcare, retail, food service, and general service sectors. Notably, while many studies incorporate skill types and levels, fewer consider employee preferences or break placement.

Table 1 Comparison of workforce scheduling models highlighting key features

Our paper addresses a hierarchical tour scheduling problem in a restaurant setting, considering full-time employees with varying skills and levels. Our compact integer programming model stands out by integrating multiple advanced features, including multiple overlapping shifts, weekly planning, and employee day-off and shift start preferences weighted by skill levels to ensure fairness and productivity. Furthermore, the use of Pareto optimality provides managers with insights into balancing overstaffing and understaffing. To our knowledge, this is the first study to incorporate these concerns in a dining restaurant setting, positioning our model as a robust and comprehensive approach to workforce scheduling compared to existing methods.

3 Methodology

This section outlines and formulates the worker scheduling problem. Section 3.1 provides a brief introduction to the problem and our approach. Section 3.2 details the mathematical model, explaining the stages and the Pareto frontier approach.

3.1 Problem setting

An effective labor scheduling approach is essential for managing the complexities of the service industry to maintain high service quality and ensure enterprise sustainability. These complexities include extended operating hours and fluctuating customer demand throughout the day and across the week. A well-balanced schedule ensures adequate staffing for peak times while avoiding overstaffing during slower periods.

Understaffing and overstaffing are central challenges in restaurant scheduling. When understaffing occurs, the number of employees available is insufficient to meet customer demand, resulting in delays, poor service quality, and frustrated customers. This can lead to longer waiting times, diminished customer experience, and negative online reviews, which can significantly impact the restaurant's reputation and bottom line. Conversely, overstaffing means employing more workers than necessary, leading to increased labor costs without a corresponding improvement in service. While overstaffing may alleviate some pressure during peak periods, it results in unnecessary expenses and can reduce operational efficiency.

To effectively address these challenges, it is critical for managers to identify the right balance between these two extremes. Achieving this balance is not straightforward, as the optimal solution may vary depending on factors such as customer expectations, operating hours, and available resources.

Our proposed model uses Pareto optimality to help managers balance understaffing and overstaffing. By constructing a Pareto frontier, we compare staffing solutions that represent trade-offs between these factors. Solutions on this frontier are non-dominated, meaning no solution is superior in both minimizing understaffing and overstaffing. This approach provides managers with multiple options to choose the staffing level that best fits their priorities. The aim is to balance staffing costs with customer service levels, offering a range of solutions that adapt to both predictable and unpredictable demand fluctuations.

In developing an optimal workforce schedule, it is essential to consider employee preferences, skill levels, and fairness to enhance job satisfaction and loyalty. When employees feel that their needs and skills are respected, they are more likely to stay motivated and provide high-quality service, ultimately benefiting the business. However, achieving this balance of flexibility, fairness, and cost-effectiveness is a challenge.

Nomenclature

Used in both models Sets $D$: Days of operation for restaurant, indexed by i $P$: Periods that the restaurant is open during the day, indexed by j Parameters $n$: total number of periods in a single working day $d$: the number of working days in a week for an employee $h$: the number of working hours in a day for an employee ${p}_{j}$: the proportion of the present employees actively working during period $j$, $\forall j\in P$ Used only in first stage of the model Parameters ${r}_{i,j}$: the required number of employees at period j of the day i, $\forall i\in D, j\in P$ ${c}_{1}$: constant for the second objective, which uses a minimax function to allocate employees Decision variables ${s}_{i,j}$: the number of employees that starts work at period j of the day i, $\forall i\in D, j\in P$ ${o}_{i,j}^{+}$: the number of overstaffing at period j of day i, $\forall i\in D, j\in P$ $k$: the highest number of overstaffing in all periods of the week $t$: the total number of employees Used only in second stage of the model Sets $E$: Restaurant employees, indexed by $e$ $Z$: Skills of employees, indexed by $z$ $L$: Skill level of employees, indexed by$l$ Parameters ${r}_{i,j,z,l}$: the number of employees having skill level $l$ of skill $z$ required at period $j$ of day $i$, $\forall i\in D, j\in P, z\in Z, l\in L$ ${s}_{i, j}$: number of employees that starts work at period $j$ of day $i$, $\forall i\in D, j\in P$ (Note that this was a decision variable in the first stage of the model) ${b}_{e, z, l}$: equal to 1 if employee $e$ has skill level l of skill $z$; otherwise, 0, $\forall e\in E, z\in Z, l\in L$ ${f}_{e, j}$: preference order of staff $e$ for starting work at period $j$, $\forall e\in E, j\in P$ ${g}_{e,i}$: preference order of staff $e$ for taking a day-off on day $i$, $\forall e\in E, i\in D$ ${y}_{e}$: fairness score for staff $e, \forall e\in E$ ${u}_{e}$: skill level of staff $e, \forall e\in E$ ${c}_{2}$: constant for the second objective ${c}_{3}$: constant for the third objective Decision variables ${x}_{e,i,j}$: equal to 1 if employee $e$ starts work at period $j$ of day $i$; otherwise, 0, $\forall \text{ e}\in E, i\in D, j\in P$ ${a}_{i,j,z,l}$: understaffing at period $j$ of day $i$ for skill level $l$ of skill $z, \forall i\in D, j\in P, z\in Z, l\in L$ ${v}_{e,i}$: −1 if staff $e$ take day $i$ off, otherwise 0, $\forall e\in E, i\in D$

3.2 Mathematical modelling approach

This study addresses the employee scheduling problem in service settings, where labor demands are variable and multiple factors—such as skills, preferences, and fairness—need to be integrated. To meet these requirements, we propose a two-stage model. The first stage determines the optimal workforce size to meet anticipated customer demand, while the second stage allocates specific shifts based on employee day-off and shift preferences, skills and skill levels, and prior scheduling fairness.

Our use of a two-stage approach, with a Pareto optimality step in between, is driven not by a desire to simplify the model but by real-world operational needs. These two stages must be solved at different time intervals to reflect the realities of staffing decisions. In the first stage, we determine the optimal staff size needed to meet demand levels, regardless of individual employee details. The result here is an optimal number of staff rather than specific employee assignments. Before moving to the second stage, a Pareto frontier approach provides managers with a range of non-dominated staffing solutions, each balancing the trade-off between overstaffing and understaffing, allowing management to select a preferred balance point.

This staffing solution, however, is only a preliminary figure. Stage Two requires knowledge of specific individuals—such as their skills, experience, and preferences—to assign employees to specific shifts. Since managers often lack detailed information on the preferences or qualifications of all potential employees, it is impractical to combine these two stages. The first stage, along with the Pareto analysis, can be re-evaluated only when there is a significant change in demand, while the second stage must be rerun regularly (e.g., weekly) to account for up-to-date availability, preferences of current employees, and fairness. In sum, the two-stage approach ensures that the model remains adaptable and relevant in practical settings.

3.2.1 First stage of the model

The first stage of our model aims to determine the minimum number of employees to meet labor requirements while minimizing overstaffing. This stage sets a flexible foundation for scheduling, allowing managers to adjust key parameters based on operational needs, such as the number of daily working hours, break times, and employee shift lengths. These adaptable parameters make the model versatile for a wide range of service settings.

The model includes several adjustable sets and parameters. For instance, D represents the set of working days, which, e.g. in the case of a full week: D = {1, 2, …, 7}. Similarly, each working day is divided into discrete periods (i.e. hours) for planning purposes. Breaks, represented as sets B_q, are also incorporated, with specific periods allocated for lunch and relief breaks, ensuring that only a designated proportion of employees are on break during each period.

A key parameter, p_j, indicates the proportion of employees actively working during each period j, taking into account break times. It is calculated as ${p}_{j}=1-{\sum }_{\left(q|j\in {B}_{q}\right)}{BR}_{q}$, where BR_q is the proportion of employees on break during the q^th break. This approach allows for flexibility in setting different break times across the day, as required by different operational schedules. An example calculation for p_j is provided in the case study section.

3.2.2 Objective function

The objective function in Eq. 1 has two primary goals: (1) to minimize the total number of employees required, denoted by t, and (2) to minimize the maximum surplus of staff across periods, represented by k. The parameter c₁ weights this secondary objective, balancing the importance of minimizing both the number of staff and surplus distribution. In our case study, c₁ is set to 0.1, providing a practical balance between efficiency and cost.

$$\text{min } \, t + c_1 \cdot k$$

(1)

3.2.3 Constraints

Labor requirement satisfaction Eq. 2 ensures that each period’s labor demand is met by a sufficient number of employees. The total number of employees present during any period j of any workday i is expressed as $\left( {\left( {\sum\nolimits_{k = 1}^{{\min \left\{ {j,n - h + 1} \right\}}} {s_{i,k} } - \sum\nolimits_{m = 1}^{j - h} {s_{i,m} } } \right)*p_{j} } \right)$, and r_i,j is the required number of employees for that period. The difference between them is the nonnegative decision variable ${o}_{i,j}^{+}$ to track overstaffing, ensuring labor needs are always met.

$$\left( {\left( {\mathop \sum \limits_{k = 1}^{{\min \left\{ {j,n - h + 1} \right\}}} s_{i,k} - \mathop \sum \limits_{m = 1}^{j - h} s_{i,m} } \right)*p_{j} } \right) - r_{i,j} = o_{i,j}^{ + } \forall i \in D,j \in P$$

(2)

For instance, in a setting where there are 16 periods in a day (n = 16) and each employee works for 10 periods per day (h = 10), the equation for period 12 on a particular day i translates as follows:

$$\left( {\sum\limits_{k = 1}^{{\min \left\{ {12,16 - 10 + 1} \right\}}} {s_{i,k} } - \sum\limits_{m = 1}^{12 - 10} {s_{i,m} } } \right)*p_{12} - r_{i,12} = o_{i,12}^{ + }$$

This expands to:

$$\left( {s_{i,1} + s_{i,2} + s_{i,3} + s_{i,4} + s_{i,5} + s_{i,6} + s_{i,7} - \left( {s_{i,1} + s_{i,2} } \right)} \right) \, \times p_{12} - r_{i,12} = o_{(i,12)}^{ + }$$

This equation captures the number of active employees compared to the demand in period 12, ensuring any excess is tracked as ${o}_{i,12}^{+}$.

Total employee count Eq. 3 specifies that the total number of employees scheduled to start work across the scheduling period must equal the total staff t multiplied by the number of workdays per employee per scheduling period, d. For cases where each employee works six days with one day-off per scheduling period, d is set to 6.

$$\sum\limits_{i \in D,j \in P} {s_{i,j} } = d*t$$

(3)

Daily shift limits Eq. 4 ensures that, for each day within the scheduling interval, the total number of employees starting work does not exceed the total staff size t and can reach t if no employee takes a day-off. Thus, the total number of employees scheduled to start work each day must equal the total workforce minus those who are off for the day.

$$\sum\limits_{j \in P} {s_{i,j} } \le t\quad \forall i \in D$$

(4)

Overstaffing distribution Eq. 5 is used alongside the minimax part of the objective function. The difference between the number of employees actively working and the labor requirements represents overstaffing. Equation 5 ensures that overstaffing across all periods in the scheduling period remains within the decision variable k. This variable k tracks the largest overstaffing across periods. By minimizing k in the objective function, the model promotes a uniform distribution of overstaffing throughout the scheduling interval.

$$o_{i,j}^{ + } \le k\quad \forall i \in D,j \in P$$

(5)

Integer requirements Eq. 6 ensures that the total staff count and the number of employees starting their shift in each period of each day is an integer.

$$\begin{gathered} s_{i,j} \in {\mathbb{N}}\quad \forall i \in D,j \in P \hfill \\ t \in {\mathbb{N}} \hfill \\ \end{gathered}$$

(6)

3.2.4 Pareto Frontier approach

The Pareto frontier approach bridges the first and second stages of the model, offering management a spectrum of non-dominated staffing solutions that balance overstaffing and understaffing. This frontier presents a trade-off, where each point represents a unique balance between the two extremes: on one end, the fully staffed solution from the first stage with no understaffing but potential overstaffing; on the other, scenarios that reduce staffing levels but allow controlled understaffing. Since the first stage of our model inherently avoids understaffing, its optimal solution represents an extreme point on the Pareto frontier, where only overstaffing exists.

To explore other non-dominated solutions along the Pareto frontier, the ε-constraint method is employed. This technique transforms a multi-objective problem into a series of single-objective problems by treating all but one objective as constraints. Each resulting single-objective problem is then solved using linear programming. By systematically adjusting the ε values, different trade-offs between the objectives are explored. Iteratively changing the constraints on the non-primary objectives and solving multiple single-objective problems with varying ε values allows us to identify a diverse set of Pareto-optimal solutions.

To apply the ε-constraint method and determine the Pareto frontier, three adjustments to the model are introduced:

• Introducing understaffing as a variable we add a nonnegative decision variable, ${o}_{i,j}^{-}$, to the model. This variable is subtracted from the right-hand side of Eq. 2, allowing and tracking understaffing in each period j of day i.

• Iterative reduction of total staffing to explore the trade-off between under and overstaffing, the total number of employees (t), originally an objective in the first-stage model, is now treated as a constraint. Starting from the optimal full-staff solution obtained in the first stage, the total workforce is iteratively reduced by one employee in each step. This iterative process allows for a rapid exploration of the Pareto frontier, with each step requiring only a few seconds of computation time.

• Revised objective function the first part of the objective function is adjusted to minimize total understaffing for each alternative solution, min $\sum_{i\in D,j\in P}{o}_{i,j}^{-}$. This modification enables the model to generate a range of solutions along the Pareto frontier, each representing a unique trade-off between overstaffing and understaffing.

By generating this frontier, the model provides managers with insights into the optimal workforce level to balance costs with service quality. Each non-dominated solution allows management to weigh the quantifiable costs of overstaffing against the potentially less tangible but impactful consequences of understaffing, such as customer satisfaction and service delays. Once the manager decides on a solution from the Pareto frontier, it serves as the input for the second stage of the model.

3.2.5 Second stage of the model

In this stage, the specified workforce size, t, along with the number of employees starting work at each period of each day, s_i,j, from the chosen Pareto solution, are used to assign shifts to individual employees based on their skills, preferences, and skill levels, ensuring a fair and efficient scheduling process.

Here, E represents the set of current employees, each of whom may possess multiple skills and skill levels. An employee’s skills and skill levels are represented by the binary variable ${\text{b}}_{e\in E,z\in Z,l\in L}$, where Z and L denote the sets of skills and skill levels, respectively. For instance, a restaurant employee might be qualified as a waiter (skill level: apprentice) and as a griller (skill level: master), providing flexibility in role assignments.

The variable ${r}_{i,j,z,l}$ specifies the labor requirements, indicating the number of employees needed for each skill z and skill level l during period j of day i. This allows staffing to be tailored to specific operational demands, such as requiring more breakfast preparation staff in the morning and more grillers during the afternoon.

3.2.6 Constraints

Skill requirement satisfaction Eq. 7 ensures that labor requirements for each skill and skill level are met as closely as possible. For every period j of every workday i in the scheduling interval, and for every skill z and skill level l, the constraint calculates the total number of employees present with the required qualifications.

This equation is similar to Eq. 2 of stage one with the addition of skill and skill levels. The first part of the left-hand side of Eq. 7 represents the total number of employees with skill z and skill level l actively working during period j of day i, adjusted for breaks using p_j, where p_j denotes the proportion of present employees actively working during period j.

The variable ${r}_{i,j,z,l}$ indicates the labor requirement for the same skill and skill level during the given period. If the difference between the required employees and the total active employees is positive (indicating understaffing), it is tracked by the nonnegative accounting variable ${a}_{i,j,z,l}$, which the objective function seeks to minimize

$$\left( {\mathop \sum \limits_{e \in E} \sum\limits_{k = 1}^{{\min \left\{ {j,n - h + 1} \right\}}} {x_{e,i,k} } *b_{e,z,l} - \mathop \sum \limits_{e \in E} \sum\limits_{m = 1}^{j - h} {x_{e,i,m} } *b_{e,z,l} } \right)*p_{j} + a_{i,j,z,l} \ge r_{i,j,z,l} \forall i \in D,j \in P, z \in Z,l \in L$$

(7)

Alignment with stage 1 staffing levels Eq. 8 ensures that the number of employees starting work in each period of the scheduling interval aligns with the staffing levels determined by the user selected Pareto solution. This guarantees consistency between the two stages.

$$\sum\limits_{e \in E} {x_{e,i,j} } = s_{i,j} \quad \forall i \in D,j \in P$$

(8)

Shift and workday constraints Eq. 9 collectively ensure proper scheduling of employee shifts and workdays. The first part of Eq. 9 restricts each employee to start work only once per day, preventing overlapping or multiple shifts within a single day. The second part of Eq. 9 enforces the weekly workday limit, ensuring that no employee works more days than the defined maximum for the scheduling period. The parameter d, representing the maximum number of working days, can be adjusted based on the organization’s policies or operational requirements.

$$\begin{array}{*{20}l} {\sum\limits_{j \in P} {x_{e,i,j} \le 1} } \hfill & {\forall i \in D,e \in E} \hfill \\ {\sum\limits_{i \in D,j \in P} {x_{e,i,j} \le d} } \hfill & {\forall e \in E} \hfill \\ \end{array}$$

(9)

Day-off and variable constraints Eq. 10 tracks each employee's day-off, using the variable, v_e,i, which takes a value of -1 if employee e is off on day i, and 0 if he/she is working that day. Equation 11 defines x_e,i,j as a binary variable, indicating whether employee e starts work during period j of day i. Equation 12 ensures that v_e,i is a free variable, restricted to values of either 0 or -1, enabling tracking of day-off assignments.

$$v_{e,i} = \sum\limits_{j \in P} {x_{e,i,j} } - 1\quad \forall e \in E,i \in D$$

(10)

$$x_{e,i,j} \in \left\{ {0,1} \right\} \quad \forall e \in E,i \in D, j \in P$$

(11)

$$v_{e,i} \in {\mathbb{Z}} \quad \forall e \in E,i \in D$$

(12)

3.2.7 Objective function

$$\min \sum\limits_{{\begin{array}{*{20}c} {i \in D,j \in P} \\ {z \in Z,l \in L} \\ \end{array} }} {a_{i,j,z,l} } + u_{e} *y_{e} *\left( {c_{2} *\sum\limits_{{\begin{array}{*{20}c} {e \in E,i \in D} \\ {j \in P} \\ \end{array} }} {x_{e,i,j} *f_{e,j} - c_{3} *} \sum\limits_{e \in E,i \in D} {g_{e,i} *v_{e,i} } } \right)$$

(13)

Equation 13 defines the objective function for the second stage of the mathematical model, which consists of two main components: minimizing understaffing across skills and skill levels and incorporating employee preferences for shift start times and days off.

The primary objective of the second stage is to minimize understaffing, represented by the variable ${a}_{i,j,z,l}$. This variable tracks any unmet staffing needs by skill z and skill level l across periods j and days i. Rather than imposing a strict constraint, this goal is incorporated as a soft constraint (as in Eq. 7), allowing slight deviations in staffing levels when necessary to maintain feasible solutions.

The second component of the objective function addresses employee preferences. Employees specify their preferred start times and days off, represented by ${g}_{e,i}$ for day-off preferences and ${f}_{e,j}$ for shift start preferences. These preferences are weighted by skill levels using ${u}_{e}$, giving higher-skilled employees priority in their choices. For instance, a master-level employee's preferences are prioritized over those of an apprentice, enhancing employee loyalty and productivity.

In addition, the model employs a fairness metric, represented by the fairness score ${y}_{e}$. This score reflects prior scheduling satisfaction by averaging realized preferences over recent weeks, helping to avoid consistently assigning less desirable shifts to any particular employee. For example, if an employee’s recent day-off assignments did not align well with his/her top choices, the model adjusts to increase the likelihood of assigning them a preferred day-off in the upcoming schedules. A detailed example of fairness score calculation is provided in the case study section.

The preferences for day-offs and shift start times are further balanced against the understaffing objective using weights c₂ and c₃. In our case study, both c₂ and c₃ are set to 0.1, providing a practical balance between efficiency and cost. These weights allow the model to adjust the relative importance of minimizing understaffing versus honoring employee preferences, ensuring a flexible and adaptable scheduling solution.

4 Case study

The case study was conducted at one of the largest branches of Türkiye’s leading casual dining restaurant chain, Köfteci Yusuf. The chain employs over 9000 full-time workers, operates 254 restaurants nationwide, 134 of which follow a casual dining concept, and the remainder are fast-food establishments. The casual dining concept focuses on serving beef, lamb, and chicken as main dishes, accompanied by a variety of appetizers, salads, desserts, and non-alcoholic beverages. Additionally, the restaurants feature boutique markets with butcher and deli sections and offer takeaway services. Due to the chain’s reasonable pricing, customer traffic is consistently high, often leading to long queues, especially during weekend peak hours. To maintain customer satisfaction and operational efficiency, it is crucial to optimize staffing levels in alignment with fluctuating demand.

The selected branch for this case study, the Karaman, Bursa branch, exemplifies these challenges. It is one of the largest branches, employing approximately 150 staff. This branch operates for 16 h daily, opening at 8:00 AM and closing at midnight. The current scheduling system has four fixed starting times (8:00, 10:00, 12:00, and 14:00) where each shift is 10 h including 1 h break.

In our model, the workday is divided into 16 one-hour periods, with employees working 10-h shifts (ℎ = 10). Employees may start their shifts hourly, with the latest possible start time being period 7 (n − ℎ + 1 = 7, as referenced in Eqs. 2 and 7) to ensure all shifts end by the close of the operating day.

To accommodate breaks, two distinct periods are allocated daily. The first break (lunch) spans four periods (periods 6 to 9, or 1:00 PM to 4:00 PM), and the second break (relief) spans four periods (periods 10 to 13, or 5:00 PM to 8:00 PM). During the lunch break, each employee takes a 40-min break (equivalent to 0.67 periods). Consequently, the proportion of employees on break during periods 6, 7, 8, and 9 (${BR}_{1}$) is 0.67/4 = 0.17, meaning that 83% of the present employees actively work during this break. Similarly, during the relief break, each employee takes a 20-min break (equivalent to 0.33 periods), resulting in a break proportion of 0.33/4 = 0.08 for periods 10, 11, 12, and 13 (${BR}_{2}$). Thus, 92% of the present employees actively work during the relief break times. Note that, although we assume that breaks are distributed uniformly, in practice the manager decides which employees will take breaks based on operational needs.

Table 2 illustrates this example, where ${BR}_{1}$ and ${BR}_{2}$ represent the proportion of present employees on break during the lunch and relief periods, respectively, and ${p}_{j}$ (see Eqs. 2 and 7) denotes the proportion of present employees actively working during period j. Although the model permits overlapping break periods, the case study doesn’t have overlapping breaks.

Table 2 Percentages of staff on break and actively working during designated break periods (Note that first break periods are 6 to 9 and second break periods are 10 to 13.)

Customer demand fluctuates significantly throughout the day and across the week, creating variable labor requirements that highlight the need for effective employee scheduling. Due to this fact, planning begins with determining labor requirements, which were calculated in detail as part of this study. While the full methodology for calculating labor requirements is beyond the scope of this article, the process is briefly described below.

Eleven distinct service roles (skill types) are defined within the restaurant: wait staff, dish-washers, grillers, cashiers, butchers, support staff, and personnel for tea, salad, dessert, breakfast, and takeaway preparation. To determine labor requirements for each role, firstly method studies were conducted to standardize all work procedures. This study took about four months, and as the result, all processes for all service roles were standardized and documented. Direct time studies were then carried out to measure the observed times for these standardized tasks. These observed times were adjusted using performance coefficients to calculate normal times. Standard times were subsequently determined by adding a 5% personal allowance and allowances for fatigue and delays to the calculated normal times. Fatigue allowances were based on task difficulty, as recommended by the International Labour Organization, while delay allowances, which account for non-cycle activities, were derived using work sampling techniques (Niebel and Freivalds 2014).

The calculated standard times were then used to determine staff requirements for each role. For example, in the griller role, employees work in pairs to grill meatballs, with the efficiency increasing at higher volumes. The first pair grills 18 kg of meatballs per hour, the second 22 kg, and subsequent pairs 26 kg each. For grilled meat, employees work individually, with the first employee grilling 14 kg per hour, the second 17 kg, and the rest 20 kg each.

To illustrate, if the point-of-sale (POS) system records sales of 98 kg of meatballs and 19 kg of grilled meat for a given hour, the labor requirements for the griller role are calculated as follows: POS data for dine-in orders are adjusted backward by 30 min to account for the average time between customer order and payment, while takeaway orders are not adjusted. In this case, 12 grillers would be needed, of which 10 for meatballs and 2 for grilled meat.

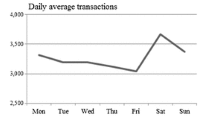
The required number of employees for each skill role during a specific period of a particular day is calculated individually. These calculated values are used as a base in both stages of the model. The labor requirements for each skill are then evaluated by management and categorized by skill levels (as represented by ${r}_{i,j,z,l}$ in Eq. 7) for use in the second stage of the problem. Additionally, these requirements are summed across all skills to determine the total labor requirement for a particular period (${r}_{i,j}$ in Eq. 2) for use in the first stage of the model. Figure 1a and b illustrate these calculated labor requirements for the first stage, based on data collected over one week in January.

Fig. 1

a Avg. labor requirements by hours of a day. b Avg. labor requirements by days of a week

Although the restaurant employs approximately 150 staff, only 121 of them (n(E) = 121) were considered during the optimization case study. This workforce size was based on the first-stage model's suggestion of 121 employees, chosen to demonstrate the model’s efficiency. The selected employees were those with multiple skills or higher skill levels, as they provide greater scheduling flexibility and operational efficiency.

So, in the study case, the restaurant employs 121 full-time staff (n(E) = 121) with varying skill sets (Z) and skill levels (L). Each skill is categorized into two levels: i.e. l = {1: apprentice, 2: master}. The number of required master-level employees for each period is determined by management and incorporated into the labor requirements. This is based on an evaluation of the labor requirements initially calculated using work measurement techniques. Employees with higher skill levels can substitute for lower-level roles, but the reverse is not allowed. This is implemented by defining all b_e,z,l and r_i,j,z,l values such that master-level workers are also classified as apprentice-level workers, and the requirements for master-level skills are added to the corresponding apprentice-level requirements.

Employees are asked to rank their preferences for shift start times (one of the seven shifts) and weekly day-offs on a scale of 1–7, where 1 indicates the most preferred option. These preferences are stored in g_e,i for day-offs and f_e,j for shifts. The model incorporates these preferences, prioritizing those of master-level employees to enhance productivity and loyalty. If an employee possesses multiple skills, their highest skill level determines their priority ranking (u_e).

Table 3 illustrates the labor requirements for different skills and skill levels on a typical Monday.

Table 3 Required number of employees of different skills and skill levels on Mondays

Additionally, a fairness metric (y_e) is employed to promote equitable scheduling by minimizing dissatisfaction with shift and day-off assignments. This metric measures the dissatisfaction level of an employee based on their previous weeks’ shift assignments. Although it can be defined in various ways, in this study, it is calculated as the average of an employee's realized preferences for day-offs and shifts over the previous four weeks.

For example, if staff e took their day-off on Wednesday in week 1 (3rd choice), Thursday in week 2 (4th choice), Sunday in week 3 (1st choice), and Monday in week 4 (5th choice), their fairness score for day-offs in week 5 would be 3.25 ((3 + 4 + 1 + 5)/4). The shift fairness score is computed similarly, and the two scores are averaged to determine the final fairness score (y_e) for scheduling in the following week.

As a company policy, part-time employment is limited, and part-time worker options were not considered during the initial planning phase. However, during the second stage of the model, the potential need for part-time workers can be assessed after all full-time employees have been allocated to tasks and shifts.

4.1 Results

The model was coded in Xpress IVE and executed on a PC running Windows with an Intel Core i5 CPU and 16 GB of RAM. The results were achieved within practical running times for the case study, demonstrating the model’s efficiency and scalability.

In the first stage, the optimal labor requirements for each period were determined in less than a second (0.1 s). These values serve as the foundation for allocating employees with the required qualifications across periods and days in the second stage.

The Pareto frontier approach was applied between the first and second stages of the model to provide management with insights into the trade-offs between overstaffing and understaffing. Figure 2 illustrates the Pareto frontier, with understaffing and overstaffing percentages plotted for various workforce sizes. In the case study, the first-stage model identified 121 employees as the optimal workforce size, ensuring no understaffing. This solution lies at one extreme of the Pareto frontier, representing zero understaffing but with a 17% overstaffing rate, calculated as the total overstaffing hours divided by total employee work hours. The minimax formulation in the first stage objective function ensures that overstaffing is distributed uniformly across the scheduling interval through the decision variable k. In contrast, a 77-employee solution eliminates any overstaffing but results in a 23% understaffing rate, occupying the opposite end of the Pareto frontier.

Fig. 2

Understaffing versus overstaffing Pareto frontier for the case study. The values are given in percentages for ease of reading

Figure 3 compares the 121-employee solution with a reasonable solution i.e. 109 employees. The 109-employee solution exhibits both overstaffing and understaffing. The solid black line represents labor requirements, the red dashed line shows the 109-employee solution, and the long blue dashed line represents the 121-employee solution. The restaurant’s policy of prohibiting understaffing for maximum customer satisfaction guided the decision to adopt the 121-employee solution for the second stage. While the Pareto frontier approach offers flexibility, the decision to prioritize the 121-employee solution reflects the higher uncertainty and harder-to-quantify impacts of understaffing, such as reduced customer satisfaction and potential revenue loss.

Fig. 3

Number of employees for two Pareto-optimal solutions vs. requirement during the days of the week

The results presented here do not account for absenteeism. Considering the company’s average historical absenteeism rate of 8%, the effective workforce of 150 employees is equivalent to 138 full-time employees for our model.

Compared to the existing manual scheduling system, the 121-employee solution offers significant improvement. By eliminating understaffing altogether, it ensures consistent service quality and customer satisfaction. Furthermore, this optimized schedule achieves a 12.3% reduction in labor costs, demonstrating the potential for substantial savings. The manual scheduling system, constrained by four fixed starting times (8:00, 10:00, 12:00, and 14:00), struggles to adapt to fluctuating demand throughout the day. This rigidity often results in understaffing during peak hours, even when employing a larger workforce. This result shows the effectiveness of the first stage of the model to balance workforce requirements.

The second stage of the model uses the 121-employee solution as input to generate detailed schedules. Each employee's work schedule is optimized based on their skills, skill levels, and preferences for day-off and shift start times in just a few seconds (3.1 s for this case study). Figure 4 presents a sample schedule for Mondays.

Fig. 4

Workforce schedule for Mondays

Employees are assigned one day-off per week, and the fulfillment rates for day-off preferences by skill level are shown in Table 4. Master workers’ preferences are prioritized, as indicated by the parameter u_s, set to 1 for apprentices and 2 for masters. While Sundays (66.9%) and Saturdays (62%) are the preferred rest days, the high labor requirements on weekends mean these preferences are often unmet. Overall, 82.0% of master workers and 73.2% of apprentices are assigned to one of their top three day-off choices. Management can further adjust the prioritization of preferences by modifying u_s and c₃.

Table 4 Fulfillment rate of day-off and shift start preferences vs. skill levels of employees

The fulfillment rates for shift start time preferences by skill level are also shown in Table 4. Most employees prefer earlier shifts, such as 8:00 AM (16.5%), 9:00 AM (22.3%), or 10:00 AM (20.7%). Among master workers, 60.3% are assigned their first choice, 21.4% their second choice, and 3.8% their third choice. For apprentices, these percentages are lower for the first and second choices, but 71.7% are assigned to one of their top three choices.

Another key objective of the second stage is minimizing understaffing for each skill and skill level. While the first stage guarantees that overall labor requirements are met, the second stage allows for minor skill-specific shortages. This is due to potential limitations in the current workforce’s skill set. Across the week, the model results show 16.55 person-hours of understaffing, primarily concentrated in specific skills: 6.8 h for dishwashers, 4.16 h for grillers, 2.24 h for takeaway, 1.23 h for cashiers, 1.23 h for butchers, and 0.8 h for dessert preparation. Notably, the majority of this understaffing occurs at the master skill level. To optimize staffing, it is advisable to employ multi-skilled workers or hire part-time staff to address these understaffed areas. The understaffing data provided by the model can guide management in making informed decisions about workforce planning, recruitment, and training.

5 Discussion & conclusions

Service industries face a significant challenge in managing fluctuating customer demand throughout the day and week. Effectively addressing this challenge requires careful consideration of employee preferences and skills to maintain both morale and productivity. This paper presents a two-stage integer programming model that can be used as a shift and day-off scheduler for service organizations. The proposed model first determines the optimal number of employees for each starting period of each day throughout the week. Subsequently, it assigns the required number of employees to tasks based on their skills, skill levels, and shift and day-off preferences. Note that we modeled shifts and breaks implicitly, leading to fewer decision variables and reduced computation time.

We use real data from a dining restaurant chain to test the proposed model and demonstrate its value in improving costs and labor satisfaction. Labor costs are reduced by 12.3% compared to the existing manual scheduling.

The second stage of the model minimizes skill-specific understaffing, revealing only a total of 16.55 person-hours of shortages in a week across various skills, mostly at the master level. This data can guide management in workforce planning, suggesting the need for multi-skilled workers or part-time staff to fill gaps.

Our study highlights notably high percentages in the fulfillment of both day-off and shift preferences. Specifically, 82.0% of master employees receive one of their top three choices for days off, and 85.5% have their preferred shifts. For apprentices, 73.2% receive one of their top three choices for days off, while 71.7% have their preferred shifts. Nevertheless, if an employee’s recent preferences do not align well with their top choices, the model adjusts to increase the likelihood of assigning him/her a preferred one in the upcoming schedules. These high fulfillment rates underscore the effectiveness of considering employees' preferences, which likely enhances their job satisfaction and retention—key factors for maintaining a skilled workforce. Additionally, the higher fulfillment rate for master employees is due to the prioritization of their preferences.

5.1 Practical implications

Restaurants experience highly variable demand, requiring flexible scheduling. Creating manual work schedules takes a lot of time and effort, especially in industries where there are many employees and flexibility is needed. Research by Glover and McMillan (1986) shows that manually scheduling 70–100 employees can take 8–14 h per week, keeping managers from other crucial duties.

Our model assists service managers in making staffing and scheduling decisions by identifying the trade-offs between overstaffing, which increases labor costs without enhancing customer service, and understaffing, which leads to poor service and negative reviews. By determining the optimal balance between labor costs and overall service levels through a Pareto frontier, managers can position their services competitively.

Moreover, considering employee preferences boosts their morale, motivation, and productivity. When employees feel their needs and preferences are taken into account, they are more likely to be satisfied with their job and committed to the company, leading to improved service levels.

5.2 Limitations and future research

Regarding the study’s limitations, it must be recognized that the analysis was restricted to data collected from a restaurant for a limited time. With a naïve approach, we assume the following week's demand will be similar to the previous week’s. This approach is only applicable when there is no holiday or special events. However, the manager may use the previous year’s holiday data in combination with a trend to forecast an upcoming holiday demand.

Another limitation of applying the model is that gathering data about employee preferences can sometimes be challenging. However, it is crucial to renew schedules periodically since the choices and availability of the employees may change over time. Nevertheless, the manager can collect employee preferences and transfer them into our scheduling model using a mobile application. With the help of the mobile application, employees with the same skills can also swap their days and shifts. The advantages of such a system can directly affect the manager's satisfaction with the operations.

Future studies could consider employees' task choices and preferred coworkers. Additionally, shift assignments could consider consecutive days; for instance, employees working late shifts may prefer not to work early the next day. The model can also be easily adapted to include full-time and part-time employees.

Lastly, although our paper focuses on a hierarchical tour scheduling problem for a restaurant, the proposed model can be applied to various service areas such as hotels, retail stores, call centers, and amusement parks, all of which experience fluctuating customer demand.