Skip to main content

Advertisement

SpringerLink
Log in

Hierarchical Human Machine Interaction Learning for a Lower Extremity Augmentation Device

  • Published:
International Journal of Social Robotics Aims and scope Submit manuscript

Abstract

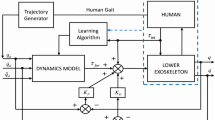
For several years considerable effort has been devoted to the study of human augmentation robots. Traditionally, the focus of exoskeleton system has always been on model-based control framework. It seeks to model the dynamic system from prior knowledge of the robot as well as the pilot. However, in lower extremity exoskeleton, the control method depends on not only the modelling accuracy but also the physical human–machine interaction changed from personal physical conditions. To address this problem, in this paper, we present a model-free incremental human–machine interaction learning methodology. In a higher level, the methodology can plan the motion of exoskeleton with the sequence of rhythmic movement primitives. In the lower level, the gain scheming is updated from the dynamic system based on a novel proposed learning algorithm efficient \(PI^2\)-CMA-ES. Compared with \(PI^{BB}\), a particular feature is that it directly operates on the Cholesky decomposition of the covariance matrix, reducing the computational effort from \(O(n^3)\) to \(O(n^2)\). To evaluate our proposed methodology, we not only demonstrate its applications on the single leg exoskeleton platform but also test on our lower extremity augmentation device. Experimental results show that the proposed methodology can minimize the interaction between the pilot and the exoskeleton compared with the traditional model-based control strategy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Cherry MS, Kota S, Young A, Ferris DP (2016) Running with an elastic lower limb exoskeleton. J Appl Biomech 32(3):269

    Article  Google Scholar 

  2. In H, Jeong U, Lee H, Cho KJ (2017) A novel slack enabling tendon drive that improves efficiency, size, and safety in soft wearable robots. IEEE ASME Trans Mechatron 22(1):59–70

    Article  Google Scholar 

  3. Ortiz J, Rocon E, Power V, de Eyto A, O’Sullivan L, Wirz M, Bauer C, Schülein S, Stadler K S, Mazzolai B, et al (2017) XoSoft–a vision for a soft modular lower limb exoskeleton. Wearable robotics: challenges and trends. Springer, Cham, pp 83–88

  4. Wang L, Du Z, Dong W, Shen Y, Zhao G (2018) Probabilistic sensitivity amplification control for lower extremity exoskeleton. Appl Sci 8(4):525

    Article  Google Scholar 

  5. Wang L, Du Z, Dong W, Shen Y, Zhao G (2018) Intrinsic sensing and evolving internal model control of compact elastic module for a lower extremity exoskeleton. Sensors 18(3):909

    Article  Google Scholar 

  6. Yu W, Rosen J, Li X (2011) PID admittance control for an upper limb exoskeleton. In: Proceedings of the 2011 American control conference, pp 1124–1129. IEEE

  7. Lee S, Sankai Y (2002) Power assist control for walking aid with HAL-3 based on EMG and impedance adjustment around knee joint. In: IEEE/RSJ international conference on intelligent robots and systems, 2002, vol. 2, pp 1499–1504. IEEE

  8. Tran HT, Cheng H, Duong MK, Zheng H (2014) Fuzzy-based impedance regulation for control of the coupled human-exoskeleton system. In: 2014 IEEE international conference on robotics and biomimetics (ROBIO), pp 986–992. IEEE

  9. Aguirre-Ollinger G, Colgate JE, Peshkin MA, Goswami A (2007) Active-impedance control of a lower-limb assistive exoskeleton. In: 2007 IEEE 10th international conference on rehabilitation robotics, pp 188–195. IEEE

  10. Kazerooni H, Racine J L, Huang L, Steger R (2005) On the control of the Berkeley lower extremity exoskeleton (BLEEX). In: Proceedings of the 2005 IEEE international conference on robotics and automation, pp 4353–4360. IEEE

  11. Kazerooni H, Chu A, Steger R (2007) That which does not stabilize, will only make us stronger. Int J Robot Res 26(1):75

    Article  MATH  Google Scholar 

  12. Ghan J, Steger R, Kazerooni H (2006) Control and system identification for the Berkeley lower extremity exoskeleton (BLEEX). Adv Robot 20(9):989

    Article  Google Scholar 

  13. Mitrovic D, Klanke S, Howard M, Vijayakumar S (2010) Exploiting sensorimotor stochasticity for learning control of variable impedance actuators. In: 2010 10th IEEE-RAS international conference on humanoid robots, pp 536–541. IEEE

  14. Siciliano B, Sciavicco L, Villani L, Oriolo G (2010) Robotics: modelling, planning and control. Springer, Berlin

    Google Scholar 

  15. Stengel RF (2012) Optimal control and estimation. Courier Corporation, North Chelmsford

    MATH  Google Scholar 

  16. Zhou K, Doyle JC, Glover K et al (1996) Robust and optimal control, vol 40. Prentice Hall, New Jersey

    MATH  Google Scholar 

  17. Sutton RS, Barto AG (1998) Reinforcement learning: an introduction. MIT Press, Cambridge

    MATH  Google Scholar 

  18. Huang R, Cheng H, Guo H, Chen Q, Lin X (2016) Hierarchical interactive learning for a human-powered augmentation lower exoskeleton. In: 2016 IEEE international conference on robotics and automation (ICRA), pp 257–263. IEEE

  19. Huang R, Cheng H, Guo H, Lin X, Zhang J (2017) Hierarchical learning control with physical human–exoskeleton interaction. Information Sciences, London

    Google Scholar 

  20. Veneman JF, Kruidhof R, Hekman EE, Ekkelenkamp R, Van Asseldonk EH, Van Der Kooij H (2007) Design and evaluation of the LOPES exoskeleton robot for interactive gait rehabilitation. IEEE Trans Neural Syst Rehabil Eng 15(3):379

    Article  Google Scholar 

  21. Hogan N (1984) Impedance control: an approach to manipulation. In: American control conference, 1984, pp 304–313. IEEE

  22. Hogan N (1985) Impedance control: an approach to manipulation: part II—implementation. J Dyn Syst Meas Control 107(1):8

    Article  MATH  Google Scholar 

  23. Huang H, Crouch DL, Liu M, Sawicki GS, Wang D (2016) A cyber expert system for auto-tuning powered prosthesis impedance control parameters. Ann Biomed Eng 44(5):1613

    Article  Google Scholar 

  24. Alqaudi B, Modares H, Ranatunga I, Tousif SM, Lewis FL, Popa DO (2016) Model reference adaptive impedance control for physical human–robot interaction. Control Theory Technol 14(1):68

    Article  MathSciNet  MATH  Google Scholar 

  25. Jacobson D, Mayne D (1970) Differential dynamic programming. Elsevier, Amsterdam

    MATH  Google Scholar 

  26. Lantoine G, Russell RP (2008) A hybrid differential dynamic programming algorithm for robust low-thrust optimization. In: AAS/AIAA astrodynamics specialist conference and exhibit, pp 152–173

  27. Morimoto J, Atkeson CG (2003) Minimax differential dynamic programming: an application to robust biped walking. IEEE Press, London

    Google Scholar 

  28. Tassa Y, Erez T, Smart WD (2008)Receding horizon differential dynamic programming. In: Advances in neural information processing systems, pp 1465–1472

  29. Li W, Todorov E (2004) Iterative linear quadratic regulator design for nonlinear biological movement systems. In: ICINCO(1), pp 222–229

  30. Todorov E (2009) Efficient computation of optimal actions. Proc Nat Acad Sci 106(28):11478

    Article  MATH  Google Scholar 

  31. Todorov E (2006) Linearly-solvable Markov decision problems. In: Advances in neural information processing systems, pp 1369–1376

  32. Todorov E (2008) General duality between optimal control and estimation. In: 47th IEEE conference on decision and control, CDC, pp 4286–4292. IEEE

  33. Williams RJ (1992) Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach Learn 8(3–4):229

    MATH  Google Scholar 

  34. Kober J, Peters JR (2009) Policy search for motor primitives in robotics. In: Advances in neural information processing systems, pp 849–856

  35. Stulp F, Sigaud O (2012) Policy improvement methods: between black-box optimization and episodic reinforcement learning, p 34

  36. Kopp C (2011) Exoskeletons for warriors of the future. Defence Today 9(2):38–40

    Google Scholar 

  37. Bucher D, Haspel G, Golowasch J, Nadim F (2000) Central pattern generators. eLS. Wiley Online Library

  38. Ijspeert AJ (2008) Central pattern generators for locomotion control in animals and robots: a review. Neural Netw 21(4):642

    Article  Google Scholar 

  39. Oliveira M, Matos V, Santos CP, Costa L (2013) Multi-objective parameter CPG optimization for gait generation of a biped robot. In: 2013 IEEE international conference on robotics and automation (ICRA), pp 3130–3135. IEEE

  40. Matsubara T, Morimoto J, Nakanishi J, Sato M, Doya K (2005) Learning sensory feedback to CPG with policy gradient for biped locomotion. In: Proceedings of the 2005 IEEE international conference on robotics and automation, pp 4164–4169. IEEE

  41. Ijspeert AJ, Nakanishi J, Hoffmann H, Pastor P, Schaal S (2013) Dynamical movement primitives: learning attractor models for motor behaviors. Neural Comput 25(2):328

    Article  MathSciNet  MATH  Google Scholar 

  42. Nakanishi J, Morimoto J, Endo G, Cheng G, Schaal S, Kawato M (2004) Learning from demonstration and adaptation of biped locomotion. Robot Auton Syst 47(2):79

    Article  Google Scholar 

  43. Buchli J, Stulp F, Theodorou E, Schaal S (2011) Learning variable impedance control. Int J Robot Res 30(7):820

    Article  Google Scholar 

  44. Stulp F, Buchli J, Ellmer A, Mistry M, Theodorou EA, Schaal S (2012) Model-free reinforcement learning of impedance control in stochastic environments. IEEE Trans Auton Ment Dev 4(4):330

    Article  Google Scholar 

  45. Wolpert DM, Ghahramani Z, Jordan MI (1995) Are arm trajectories planned in kinematic or dynamic coordinates? An adaptation study. Exp Brain Res 103(3):460

    Article  Google Scholar 

  46. Snelson E, Ghahramani Z (2006) Sparse Gaussian processes using pseudo-inputs. Adv Neural Inf Process Syst 18:1257

    Google Scholar 

  47. Ijspeert AJ (2001) A connectionist central pattern generator for the aquatic and terrestrial gaits of a simulated salamander. Biol Cybern 84(5):331

    Article  MathSciNet  Google Scholar 

  48. Theodorou E, Buchli J, Schaal S (2010) A generalized path integral control approach to reinforcement learning. J Mach Learn Res 11:3137

    MathSciNet  MATH  Google Scholar 

  49. Stulp F, Sigaud O (2012) Path integral policy improvement with covariance matrix adaptation. arXiv preprint arXiv:1206.4621

  50. Hansen N, Ostermeier A (2001) Completely derandomized self-adaptation in evolution strategies. Evol Comput 9(2):159

    Article  Google Scholar 

  51. Igel C, Suttorp T, Hansen N (2006) A computational efficient covariance matrix update and a (1+1)-CMA for evolution strategies. In: Proceedings of the 8th annual conference on genetic and evolutionary computation, pp 453–460. ACM

  52. Eigen M (1973) Ingo Rechenberg Evolutionsstrategie Optimierung technischer Systeme nach Prinzipien der biologishen Evolution. mit einem Nachwort von Manfred Eigen, Friedrich Frommann Verlag, Struttgart-Bad Cannstatt

  53. Stulp F, Schaal S (2011) Hierarchical reinforcement learning with movement primitives. In: 2011 11th IEEE-RAS international conference on humanoid robots (humanoids), pp 231–238. IEEE

  54. Kazerooni H, Steger R, Huang L (2006) Hybrid control of the Berkeley lower extremity exoskeleton (BLEEX). Int J Robot Res 25(5–6):561

    Article  Google Scholar 

  55. Theodorou E, Buchli J, Schaal S (2010) Reinforcement learning in high dimensional state spaces: a path integral approach. J Mach Learn Res 2010:3137

    MATH  Google Scholar 

Download references

Acknowledgements

We gratefully acknowledge the constructive comments and suggestions of the reviewers.

Funding

Part of this work has received funding from National Natural Science Foundation of China under Grant No. 51521003

Author information

Authors and Affiliations

  1. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin, 150080, People’s Republic of China

    Likun Wang, Zhijiang Du & Wei Dong

  2. School of Astronautics, Harbin Institute of Technology, Harbin, 150080, People’s Republic of China

    Likun Wang & Yi Shen

  3. Weapon Equipment Research Institute, China Ordnance Industries Group, Beijing, 102202, People’s Republic of China

    Guangyu Zhao

Authors
  1. Likun Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhijiang Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yi Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Guangyu Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Dong.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, L., Du, Z., Dong, W. et al. Hierarchical Human Machine Interaction Learning for a Lower Extremity Augmentation Device. Int J of Soc Robotics 11, 123–139 (2019). https://doi.org/10.1007/s12369-018-0484-5

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12369-018-0484-5

Keywords

Search

Navigation