Skip to main content
Springer Nature Link
Log in

OWA filters and forecasting models applied to electric power load time series

  • Original Paper
  • Published:
Evolving Systems Aims and scope Submit manuscript

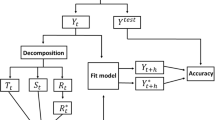
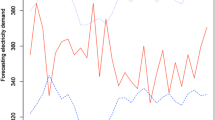
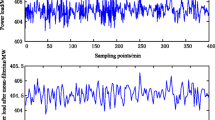
Abstract

In this paper we propose a novel approach for time series forecasting based on ordered weighted averaging operators (OWA) as linear filter and forecasting models. The OWA operators describe a family of averaging operators parameterized by the choice the weights or filter coefficients. Starting with a nonstationary time series of a given phenomenon, we evaluate the use of linear decaying and constant weights as filtering processes of time series. Moreover, we investigate the effectiveness of using exponential weighted moving average process as a filter linear. After the application of the linear operators, we formulate the best possible forecasting models, ARIMA and neural network models, for short-term forecasting for each of the new structured time series using the usual optimal procedures for a real load data from the Southest Brazilian Company. A residual analysis of these forecasting models is given. In addition, the classical ARIMA and neural network models are also developed for the subject data, and the results are compared with the proposed models that we have introduced. In all cases the new models give better short-term forecasting results than the classical models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

We’re sorry, something doesn't seem to be working properly.

Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

  1. ARIMA models were adjusted using EViews7 software.

  2. MLP models were adjusted using Matlab.

References

  • Angelov P, Zhou X (2006) Evolving fuzzy systems from data streams in real-time. In: Proceedings of the international symposium on evolving fuzzy systems-EFS’06. IEEE Press, Ambleside, pp 29–35

  • Ansley CF, Newbold P (1980) Finite sample properties of estimators for autoregressive-moving average models. J Econometr 13:159–183

    Article  MATH  Google Scholar 

  • Ballini R, Yager RR (2014) Linear decaying weights for time series smoothing: an analysis. Int J Uncertain Fuzziness Knowl Based Syst 22(1):23–40

    Article  MathSciNet  Google Scholar 

  • Box G, Jenkins GM, Reinsel GC (1994) Time series analysis, forecasting and control, 3rd edn. Holden Day, Oakland

    MATH  Google Scholar 

  • Chakravarty S, Dash P (2011) Dynamic filter weights neural network model integrated with differential evolution for day-ahead price forecasting in energy market. Exp Syst Appl 38(9):10,974–10,982

  • Chiann C, Moretin A (1998) A wavelet analysis for time series. Nonparametric Stat 10:1–46

    Article  MATH  Google Scholar 

  • Conejo AJ, Plazas MA, Espfnola R, Molina AB (2005) Day-ahead electricity price forecasting using the wavelet transform and ARIMA models. IEEE Trans Power Syst 20(2):1035–1042

    Article  Google Scholar 

  • Dickey DA, Bell WR, Miller RB (1986) Unit roots in time series models: tests and implications. Am Stat 40:12–26

    Google Scholar 

  • Diebold FX, Mariano RS (1995) Comparing predictive accuracy. J Bus Econom Stat 13(3):253–263

    Google Scholar 

  • Enders W (2009) Appl Econometr Time Series, 3rd edn. Wiley, Englewood Clifts

    Google Scholar 

  • Ghiassi M, Zimbra DK, Saidane H (2006) Medium term system load forecasting with a dynamic artificial neural network model. Electr Power Syst Res 76(5):302–316

    Article  Google Scholar 

  • Gooijer JGD, Hyndman RJ (2006) 25 years of time series forecasting. Int J Forecast 22:443–473

    Article  Google Scholar 

  • Gross G, Galiana FD (1987) Short-term load forecasting. Proc IEEE 75(12):1558–1573

    Article  Google Scholar 

  • Hippert HS, Pedreira CE, Souza RC (2001) Neural networks for short-term load forecasting: a review and evaluation. IEEE Trans Power Syst 16(1):44–55

    Article  Google Scholar 

  • Ho SL, Xie M, Goh TN (2002) A comparative study of neural netwrok and Box-Jenkins ARIMA modeling in time series prediction. Comput Ind Eng 42:371–375

    Article  Google Scholar 

  • Inglesi-Lotz R (2011) The evolution of price elasticity of electricity demand in south africa: a Kalman filter application. Energy Policy 39(6):3690–3696

    Article  Google Scholar 

  • Kalhor A, Arrabi BN, Lucas C (2012) A new systematic design for Habitually Linear Evolving TS Fuzzy Model. Expert Syst Appl 39(2):1725–1736

    Article  Google Scholar 

  • Kalman RE (1960) A new approach to linear filtering and prediction problems. J Basic Eng 82(D):35–45

  • Kandil MS, El-Debeiky SM, Hasanien NE (2002) Long-term load forecasting for fast developing utility using a knowledge-based expert system. IEEE Trans Power Syst 17(2):491–496

    Article  Google Scholar 

  • Khosravi A, Nahavandi S, Creighton D, Srinivasan D (2012) Interval type-2 fuzzy logic systems for load forecasting: a comparative study. IEEE Trans Power Syst 27(3):1274–1282

    Article  Google Scholar 

  • Lee CM, Ko CN (2011) Short-term load forecasting using lifting scheme and ARIMA models. Expert Syst. Appl 38(5):5902–5911

    Article  Google Scholar 

  • Lima E, Hell H, Ballini R, Gomide F (2010) Evolving fuzzy modeling using participatory learning. In: Angelov P, Filev D, Kasabov N (eds) Evolving intelligent systems: methodology and applications, chap 4. Wiley, Hoboken, pp 67–86

  • Maciel L, Gomide F, Ballini R (2013) Enhanced evolving participatory learning fuzzy modeling: an application for asset returns volatility forecasting. Evolv Syst 13(3):253–263

    Google Scholar 

  • Mitchell TM (1997) Machine Learning. McGraw-Hill, New York

  • Moghram I, Rahman S (1989) Analysis and Evaluation of five short-term load forecasting techniques. IEEE Trans Power Syst 4(4):1484–1491

    Article  Google Scholar 

  • Morrison GW, Pike DH (1977) Kalman Filtering applied to statistical forecasting. Manage Sci 23(7):768–774

    Article  MATH  Google Scholar 

  • Newbold P, Agiakloglou C, Miller J (1984) Adventures with ARIMA software. Int J Forecast 10:573–581

    Article  Google Scholar 

  • Nourani V, Komasi M, Mano A (2009) A multivariate ANN-wavelet approach for rainfall-runoff modeling. Water Resour Manag 23:2877–2894

    Article  Google Scholar 

  • Papadakis SE, Theocharis JB, Kiartzis SJ, Bakirtzis AG (1998) A novel approach to short-term load forecasting using fuzzy neural networks. IEEE Trans Power Syst 13(2):480–492

    Article  Google Scholar 

  • Papalexopoulos AD, Hesterberg TC (1990) A regression-based approach to short-term system load forecasting. IEEE Trans Power Syst 5(4):1535–1547

    Article  Google Scholar 

  • Renaud O, Starck JL, Murtagh F (2005) Wavelet-based combined signal filtering and prediction. IEEE Trans Syst Man Cybern Part B Cybern 35(6):1241–1251

    Article  Google Scholar 

  • Rumelhart DE, Hinton GE, Williams RJ (1986) Learning internal representations by error propagation. In: McClelland DERJL (ed) Parallel distributed processing: explorations in the microstructure of cognition, chap 8. MIT Press, Cambridge, pp 318–361

  • Said SE, Dickey DA (1984) Testing for unit roots in autoregressive-moving average models of unknown order. Biometrika 71(3):599–607

    Article  MATH  MathSciNet  Google Scholar 

  • Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6:461–464

    Article  MATH  Google Scholar 

  • Shaker A, Hüllermeier E (2012) IBLStreams: a system for instance-based classification and regression on data streams. Evolv Syst 3(4):235–249

    Article  Google Scholar 

  • Taylor JW (2012) Short-term load forecasting with exponentially weighted methods. IEEE Trans Power Syst 27(1):458–464

    Article  Google Scholar 

  • Waddi AA, Ismail MT, Alkhahazaleh MH, Karim SAA (2011) Selecting wavelet transforms model in forecasting financial time series data based on ARIMA model. Appl Math Sci 25(7):315–326

    Google Scholar 

  • White H (1989) Learning in artificial neural network: a statistical perspective. Neural Comput 1:425–464

    Article  Google Scholar 

  • Wong H, Ip W, Xie Z, Lui X (2003) Modeling and forecasting by wavelets, and the application to exchange rates. J Appl Stat 30(5):537–553

    Article  MATH  MathSciNet  Google Scholar 

  • Yager RR (1988) On ordered weighted averaging aggregation operators in multi-criteria decision making. IEEE Trans Syst Man Cybern SMC-18(1):183–190

  • Yager RR (2008) Time series smoothing and OWA aggregation. IEEE Trans Fuzzy Syst 16(4):994–1007

    Article  Google Scholar 

  • Yager RR, Filev DP (1999) Induced ordered weighted averaging operators. IEEE Trans Syst Man Cybern 29(2):141–150

    Article  Google Scholar 

  • Zhang BL, coggins R, Jabri MA, Dersch D, Flower B, (2001) Multiresolution foreacsting for futures trading using wavelet decompositions. IEEE Trans Neural Netw 12(4):765–775

Download references

Acknowledgments

This work has been supported by the São Paulo Research Foundation (Fapesp) and Brazilian National Research Council (CNPq). This work has also been supported by a Multidisciplinary University Research Initiative (MURI) grant (Number W911NF-09-1-0392) for “Unified Research on Network-based Hard/Soft Information Fusion”, issued by the US Army Research Office (ARO). This work has also been supported by an ONR grant for “Human Behavior Modeling Using Fuzzy and Soft Technologies”, award number N000141010121. We gratefully appreciate this support.

Author information

Authors and Affiliations

  1. Institute of Economics, University of Campinas, Campinas, 13083-857, Brazil

    R. Ballini

  2. Machine Intelligence Institute, Iona College, New Rochelle, NY, 10801, USA

    R. R. Yager

Authors
  1. R. Ballini
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. R. R. Yager
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to R. Ballini.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ballini, R., Yager, R.R. OWA filters and forecasting models applied to electric power load time series. Evolving Systems 5, 159–173 (2014). https://doi.org/10.1007/s12530-014-9112-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12530-014-9112-2

Keywords