Skip to main content
Springer Nature Link
Log in

Multiple attribute group decision making based on \(p,q\)-quasirung orthopair Bonferroni mean operators and their applications

  • Original Paper
  • Published:
Evolving Systems Aims and scope Submit manuscript

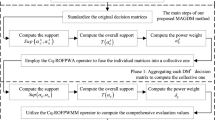
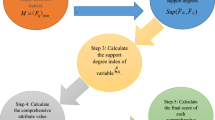
Abstract

The Bonferroni mean (BM) operator provides a strategy for justifying the effects of unrealistic aggregation values while simultaneously capturing the interconnections between input arguments. Moreover, \(p,q\)-quasirung orthopair fuzzy (\(p,q-\) -QOF) sets is a new development in fuzzy set (FS) theory that allows for more accurate and nuanced management and representation of uncertain data. In this paper, we integrate the concept of \(p,q\)-QOF numbers (\(p,q\)-QOFNs) and extend the BM operators to accommodate \(p,q\)-QOF information. To aggregate diverse preferences of decision-makers, we first present some Bonferroni mean and weighted Bonferroni mean averaging operators for \(p,q\)-QOFNs. Subsequently, we construct a decision-making (DM) framework utilizing the proposed operators within the context of \(p,q\)-QOF sittings, demonstrated through a numerical illustration. Finally, we compare the presented approach with existing methods to establish the practicality and feasibility of the proposed DM process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

This manuscript has no associated data.

References

  • Adlassnig K-P (1986) Fuzzy set theory in medical diagnosis. IEEE Trans Syst Man Cybern 16(2):260–265

    Article  MATH  Google Scholar 

  • Agilan P, Julietraja K, Mlaiki N, Mukheimer A (2022) Intuitionistic fuzzy stability of an Euler–Lagrange symmetry additive functional equation via direct and fixed point technique (FPT). Symmetry 14(11):2454

    Article  MATH  Google Scholar 

  • Akram M, Ramzan N, Feng F (2022) Extending COPRAS method with linguistic Fermatean fuzzy sets and Hamy mean operators. J Math 2022:1–26

    Article  MathSciNet  MATH  Google Scholar 

  • Amin F, Rahim M, Ali A, Ameer E (2022) Generalized cubic Pythagorean fuzzy aggregation operators and their application to multi-attribute decision-making problems. Int J Comput Intell Syst 15(1):92

    Article  MATH  Google Scholar 

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96

    Article  MATH  Google Scholar 

  • Bonferroni C (1950) Sulle medie multiple di potenze. Bollettino Dell’unione Matematica Italiana 5(3–4):267–270

    MathSciNet  MATH  Google Scholar 

  • Chakraborty S, Saha AK (2023) Novel Fermatean fuzzy Bonferroni mean aggregation operators for selecting optimal health care waste treatment technology. Eng Appl Artif Intell 119:105752

    Article  MATH  Google Scholar 

  • Chaurasiya R, Jain D (2023) Hybrid MCDM method on pythagorean fuzzy set and its application. Decis Mak Appl Manag Eng 6(1):379–398

    Article  MATH  Google Scholar 

  • Garg H (2017) Confidence levels based Pythagorean fuzzy aggregation operators and its application to decision-making process. Comput Math Organ Theory 23(4):546–571

    Article  MATH  Google Scholar 

  • Garg H (2019) New logarithmic operational laws and their aggregation operators for Pythagorean fuzzy set and their applications. Int J Intell Syst 34(1):82–106

    Article  MATH  Google Scholar 

  • Garg H, Rahim M, Amin F, Jafari S, Hezam IM (2023) Confidence levels-based cubic fermatean fuzzy aggregation operators and their application to MCDM problems. Symmetry 15(2):260

    Article  Google Scholar 

  • Jacquet-Lagrèze E (1975) How we can use the notion of semi-orders to build outranking relations in multi-criteria decision making. In: Utility, probability, and human decision making: selected proceedings of an interdisciplinary research conference, Rome, 3–6 September, 1973, Springer. pp 87–112

  • Kiker GA, Bridges TS, Varghese A, Seager TP, Linkov I (2005) Application of multicriteria decision analysis in environmental decision making. Integr Environ Assess Manag Int J 1(2):95–108

    Google Scholar 

  • Kumar K, Chen S-M (2022) Group decision making based on q-rung orthopair fuzzy weighted averaging aggregation operator of q-rung orthopair fuzzy numbers. Inf Sci 598:1–18

    Article  MATH  Google Scholar 

  • Liang D, Zhang Y, Xu Z, Darko AP (2018a) Pythagorean fuzzy Bonferroni mean aggregation operator and its accelerative calculating algorithm with the multithreading. Int J Intell Syst 33(3):615–633

    Article  MATH  Google Scholar 

  • Liang D, Darko AP, Xu Z (2018b) Interval-valued Pythagorean fuzzy extended Bonferroni mean for dealing with heterogenous relationship among attributes. Int J Intell Syst 33(7):1381–1411

    Article  MATH  Google Scholar 

  • Liu P, Liu J (2018) Some q-rung orthopai fuzzy Bonferroni mean operators and their application to multi-attribute group decision making. Int J Intell Syst 33(2):315–347

    Article  MATH  Google Scholar 

  • Liu P, Liu W (2019) Multiple-attribute group decision-making based on power Bonferroni operators of linguistic q-rung orthopair fuzzy numbers. Int J Intell Syst 34(4):652–689

    Article  MATH  Google Scholar 

  • Liu P, Tang G (2016) Some power generalized aggregation operators based on the interval neutrosophic sets and their application to decision making. J Intell Fuzzy Syst 30(5):2517–2528

    Article  MathSciNet  MATH  Google Scholar 

  • Liu P, Wang P (2018a) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J Intell Syst 33(2):259–280

    Article  MATH  Google Scholar 

  • Liu P, Wang P (2018b) Multiple-attribute decision-making based on Archimedean Bonferroni operators of q-rung orthopair fuzzy numbers. IEEE Trans Fuzzy Syst 27(5):834–848

    Article  MATH  Google Scholar 

  • Luo X, Wang Z, Yang L, Lu L, Hu S (2023) Sustainable supplier selection based on VIKOR with single-valued neutrosophic sets. PLoS ONE 18(9):e0290093

    Article  Google Scholar 

  • Ma Z, Xu Z (2016) Symmetric Pythagorean fuzzy weighted geometric/averaging operators and their application in multicriteria decision-making problems. Int J Intell Syst 31(12):1198–1219

    Article  MATH  Google Scholar 

  • Mahmood T, ur Rehman U, Ali Z, Haleemzai I (2023) Analysis of TOPSIS techniques based on bipolar complex fuzzy N-soft setting and their applications in decision-making problems. CAAI Trans Intell Technol 8(2):478–499

    Article  MATH  Google Scholar 

  • Nie RX, Tian ZP, Wang JQ, Hu JH (2019) Pythagorean fuzzy multiple criteria decision analysis based on Shapley fuzzy measures and partitioned normalized weighted Bonferroni mean operator. Int J Intell Syst 34(2):297–324

    Article  MATH  Google Scholar 

  • Paul TK, Pal M, Jana C (2021) Multi-attribute decision making method using advanced Pythagorean fuzzy weighted geometric operator and their applications for real estate company selection. Heliyon 7(6):e07340

    Article  MATH  Google Scholar 

  • Peng X, Garg H (2018) Algorithms for interval-valued fuzzy soft sets in emergency decision making based on WDBA and CODAS with new information measure. Comput Ind Eng 119:439–452

    Article  MATH  Google Scholar 

  • Qin Y, Liu Y, Abdullah S, Wei G (2021) Group decision support methodology based upon the multigranular generalized orthopair 2-tuple linguistic information model. Int J Intell Syst 36(7):3367–3400

    Article  MATH  Google Scholar 

  • Rahim M, Amin F, Ali A, Shah K (2022) An extension of Bonferroni mean under cubic Pythagorean fuzzy environment and its applications in selection-based problems. Math Probl Eng 2022:1–28

    Article  MATH  Google Scholar 

  • Seikh MR, Mandal U (2022) Multiple attribute group decision making based on quasirung orthopair fuzzy sets: application to electric vehicle charging station site selection problem. Eng Appl Artif Intell 115:105299

    Article  MATH  Google Scholar 

  • Senapati T, Yager RR (2020) Fermatean fuzzy sets. J Ambient Intell Humaniz Comput 11:663–674

    Article  MATH  Google Scholar 

  • Takeuti G, Titani S (1984) Intuitionistic fuzzy logic and intuitionistic fuzzy set theory. J Symb Log 49(3):851–866

    Article  MathSciNet  MATH  Google Scholar 

  • Talukdar P, Dutta P (2021) Distance measures for cubic Pythagorean fuzzy sets and its applications to multicriteria decision making. Granul Comput 6:267–284

    Article  MATH  Google Scholar 

  • Tan C (2011) Generalized intuitionistic fuzzy geometric aggregation operator and its application to multi-criteria group decision making. Soft Comput 15:867–876

    Article  MATH  Google Scholar 

  • Wang R (2019) Research on the application of the financial investment risk appraisal models with some interval number Muirhead mean operators. J Intell Fuzzy Syst 37(2):1741–1752

    Article  MATH  Google Scholar 

  • Wei G, Lu M (2018) Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int J Intell Syst 33(1):169–186

    Article  MATH  Google Scholar 

  • Wu L, Wang J, Gao H (2019a) Models for competiveness evaluation of tourist destination with some interval-valued intuitionistic fuzzy Hamy mean operators. J Intell Fuzzy Syst 36(6):5693–5709

    Article  MATH  Google Scholar 

  • Wu L, Gao H, Wei C (2019b) VIKOR method for financing risk assessment of rural tourism projects under interval-valued intuitionistic fuzzy environment. J Intell Fuzzy Syst 37(2):2001–2008

    Article  MATH  Google Scholar 

  • Xu Z (2007) Intuitionistic fuzzy aggregation operators. IEEE Trans Fuzzy Syst 15(6):1179–1187

    Article  MATH  Google Scholar 

  • Xu Z, Yager RR (2010) Intuitionistic fuzzy Bonferroni means. IEEE Trans Syst Man Cybern Part B (Cybern) 41(2):568–578

    MATH  Google Scholar 

  • Yager RR (2013) Pythagorean fuzzy subsets. In: 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), IEEE. pp 57–61

  • Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230

    Article  MATH  Google Scholar 

  • Yang W, Pang Y (2020) New q-rung orthopair fuzzy Bonferroni mean Dombi operators and their application in multiple attribute decision making. IEEE Access 8:50587–50610

    Article  MATH  Google Scholar 

  • Zadeh LA (1965) Information and control. Fuzzy Sets 8(3):338–353

    MATH  Google Scholar 

Download references

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large group Research Project under grant number RGP2/461/44

Funding

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large group Research Project under grant number RGP2/461/44.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Hazara University Mansehra, Khyber Pakhtunkhwa, 21300, Pakistan

    Muhammad Rahim

  2. EIAS Data Science Lab, College of Computer and Information Sciences, Prince Sultan University, 11586, Riyadh, Saudi Arabia

    Sadique Ahmad

  3. Department of Mathematics, Faculty of Arts and Science, Elmagarda, King Khalid University, Abha, Saudi Arabia

    B. A. Younis

  4. Department of Mathematics, College of Science and Humanities in Sulail, Prince Sattam Bin Abdulaziz University, Al-Kharj, Saudi Arabia

    Ria H. Egami

  5. Faculty of Sciences Department of Mathematics, The Islamic University of Madinah, Medina, Kingdom of Saudi Arabia

    Mohammed Mustafa Ahmed

Authors
  1. Muhammad Rahim
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Sadique Ahmad
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. B. A. Younis
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ria H. Egami
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Mohammed Mustafa Ahmed
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Muhammad Rahim.

Ethics declarations

Conflict of interest

The authors affirm that there are no conflicts of interest to declare.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahim, M., Ahmad, S., Younis, B.A. et al. Multiple attribute group decision making based on \(p,q\)-quasirung orthopair Bonferroni mean operators and their applications. Evolving Systems 16, 9 (2025). https://doi.org/10.1007/s12530-024-09638-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12530-024-09638-w

Keywords