Skip to main content
SpringerLink
Log in

A hybrid LP/NLP paradigm for global optimization relaxations

  • Full Length Paper
  • Published:
Mathematical Programming Computation Aims and scope Submit manuscript

Abstract

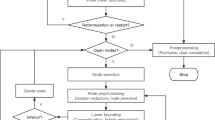
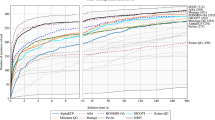
Polyhedral relaxations have been incorporated in a variety of solvers for the global optimization of mixed-integer nonlinear programs. Currently, these relaxations constitute the dominant approach in global optimization practice. In this paper, we introduce a new relaxation paradigm for global optimization. The proposed framework combines polyhedral and convex nonlinear relaxations, along with fail-safe techniques, convexity identification at each node of the branch-and-bound tree, and learning strategies for automatically selecting and switching between polyhedral and nonlinear relaxations and among different local search algorithms in different parts of the search tree. We report computational experiments with the proposed methodology on widely-used test problem collections from the literature, including 369 problems from GlobalLib, 250 problems from MINLPLib, 980 problems from PrincetonLib, and 142 problems from IBMLib. Results show that incorporating the proposed techniques in the BARON software leads to significant reductions in execution time, and increases by 30% the number of problems that are solvable to global optimality within 500 s on a standard workstation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Ahmadi, A.A., Olshevsky, A., Parrilo, P.A., Tsitsiklis, J.N.: NP-hardness of deciding convexity of quartic polynomials and related problems. Math. Program. 137, 453–476 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Avriel, M., Diewert, W.E., Schaible, S., Zang, I.: Generalized Concavity. Plenum Press, New York (1988)

    Book  MATH  Google Scholar 

  3. Bao, X.: Automatic convexity detection for global optimization. Master’s thesis, Department of Chemical Engineering, University of Illinois at Urbana-Champaign (2007)

  4. Bao, X., Khajavirad, A., Sahinidis, N.V., Tawarmalani, M.: Global optimization of nonconvex problems with multilinear intermediates. Math. Program. Comput. 7(1), 1–37 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  5. Beale, E.M.L., Forrest, J.J.H.: Global optimization using special ordered sets. Math. Program. 10, 52–69 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  6. Beale, E.M.L., Tomlin, J.A.: Special facilities in a general mathematical programming system for nonconvex problems using ordered sets of variables. In: Lawrence, J. (ed.) Proceedings of the Fifth International Conference on Operational Research, pp. 447–454. Tavistock Publications, London (1970)

    Google Scholar 

  7. Belotti, P., Lee, J., Liberti, L., Margot, F., Wächter, A.: Branching and bounds tightening techniques for non-convex MINLP. Optim. Methods Softw. 24, 597–634 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bertsekas, D.P., Yu, H.: A unifying polyhedral approximation framework for convex optimization. SIAM J. Optim. 21, 333–360 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bonami, P., Biegler, L.T., Conn, A.R., Cornuejols, G., Grossmann, I.E., Laird, C.D., Lee, J., Lodi, A., Margot, F., Sawaya, N., Wächter, A.: An algorithmic framework for convex mixed integer nonlinear programs. Discrete Optim. 5, 186–204 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  10. Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  11. Bussieck, M.R., Drud, A.S., Meeraus, A.: MINLPLib—a collection of test models for mixed-integer nonlinear programming. INFORMS J. Comput. 15, 114–119 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  12. Chinneck, J.W.: Analyzing mathematical programs using MProbe. Ann. Oper. Res. 104, 33–48 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  13. CMU-IBM open source MINLP project test set. http://egon.cheme.cmu.edu/ibm/page.htm

  14. COIN-OR Project. CBC 2.9.7 Coin Branch and Cut programming solver. https://projects.coin-or.org/Cbc

  15. COIN-OR Project. FilterSD 2 Coin FilterSD solver. https://projects.coin-or.org/filterSD

  16. Dolan, E., Moré, J.: Benchmarking optimization software with performance profiles. Math. Program. 91, 201–213 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  17. Domes, F., Neumaier, A.: Constraint propagation on quadratic constraints. Constraints 15, 404–429 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Drud, A.: CONOPT 3.17A, User’s Manual. ARKI Consulting and Development A/S, Bagsvaerd, Denmark (2016)

  19. Duran, M.A., Grossmann, I.E.: An outer-approximation algorithm for a class of mixed-integer nonlinear programs. Math. Program. 36, 307–339 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  20. Fourer, R., Maheshwari, C., Neumaier, A., Orban, D., Schichl, H.: Convexity and concavity detection in computational graphs: tree walks for convexity assessment. INFORMS J. Comput. 22, 26–43 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  21. Fourer, R., Orban, D.: DrAmpl: a meta solver for optimization problem analysis. CMS 7, 437–463 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  22. Gamrath, G., Fischer, T., Gally, T., Gleixner, A.M., Hendel, G., Koch, Th., Maher, S.J., Miltenberger, M., Müller, B., Pfetsch, M.E., Puchert, Ch., Rehfeldt, D., Schenker, S., Schwarz, R., Serrano, F., Shinano, Y., Vigerske, S., Weninger, D., Winkler, M., Witt, J.T., Witzig, J.: The scip optimization suite 3.2. Technical Report 15-60, ZIB (2016)

  23. GAMS Performance tools. http://www.gamsworld.org/performance/tools.htm. Accessed 7 May 2018

  24. GAMS/EXAMINER: User’s Manual. https://www.gams.com/latest/docs/S_EXAMINER.html. Accessed 7 May 2018

  25. GAMS/SBB: User’s Manual. https://www.gams.com/latest/docs/S_SBB.html. Accessed 7 May 2018

  26. Gill, P.E., Murray, W., Saunders, M.A.: User’s Guide for SNOPT 7: A FORTRAN Package for Large-Scale Nonlinear Programming. Technical report, University of California, San Diego and Stanford University, CA (2008)

  27. GLOBAL Library. http://www.gamsworld.org/global/globallib.htm. Accessed 7 May 2018

  28. Grant,M., Boyd, S.: CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx, (2014, March)

  29. Grant, M., Boyd, S., Ye, Y.: Disciplined convex programming. In: Liberti, L., Maculan, N. (eds.) Chapter in Global Optimization: From Theory to Implementation, Nonconvex Optimization and Its Applications, pp. 155–210. Springer, Boston, MA (2006)

    Chapter  Google Scholar 

  30. IBM: CPLEX Optimizer (2016). http://www-01.ibm.com/software/integration/optimization/cplex-optimizer/. Accessed 7 May 2018

  31. Kearfott, R.B.: GlobSol user guide. Optim. Methods Softw. 24, 687–708 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  32. Kelley, J.E.: The cutting plane method for solving convex programs. J. SIAM 8, 703–712 (1960)

    MathSciNet  MATH  Google Scholar 

  33. Lin, Y., Schrage, L.: The global solver in the LINDO API. Optim. Methods Softw. 24, 657–668 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  34. McCormick, G.P.: Computability of global solutions to factorable nonconvex programs: Part I—convex underestimating problems. Math. Program. 10, 147–175 (1976)

    Article  MATH  Google Scholar 

  35. Misener, R., Floudas, ChA: ANTIGONE: algorithms for continuous/integer global optimization of nonlinear equations. J. Global Optim. 59, 503–526 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  36. Monnigmann, M.: Efficient calculation of bounds on spectra of Hessian matrices. SIAM J. Sci. Comput. 30, 2340–2357 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  37. Murtagh, B.A., Saunders, M.A.: MINOS 5.5 User’s Guide. Technical Report SOL 83-20R, Systems Optimization Laboratory, Department of Operations Research, Stanford University, CA (1995)

  38. Nenov, I., Fylstra, D., Kolev, L.: Convexity determination in the microsoft excel solver using automatic differentiation techniques. In: The 4th International Conference on Automatic Differentiation (2004)

  39. Neumaier, A., Shcherbina, O.: Safe bounds in linear and mixed-integer linear programming. Math. Program. 99, 283–296 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  40. Princeton Library. http://www.gamsworld.org/performance/princetonlib/princetonlib.htm. Accessed 7 May 2018

  41. Rosen, J.B., Pardalos, P.M.: Global minimization of large-scale constrained concave quadratic problems by separable programming. Math. Program. 34, 163–174 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  42. Ryoo, H.S., Sahinidis, N.V.: A branch-and-reduce approach to global optimization. J. Global Optim. 8, 107–139 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  43. Sahinidis, N.V.: BARON: a general purpose global optimization software package. J. Global Optim. 8, 201–205 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  44. Sahinidis, N.V.: BARON 12.1.0: Global Optimization of Mixed-Integer Nonlinear Programs, User’s Manual (2013)

  45. Tawarmalani, M., Sahinidis, N.V.: Convexification and Global Optimization in Continuous and Mixed-Integer Nonlinear Programming: Theory, Algorithms, Software, and Applications. Kluwer Academic Publishers, Dordrecht (2002)

    Book  MATH  Google Scholar 

  46. Tawarmalani, M., Sahinidis, N.V.: Global optimization of mixed-integer nonlinear programs: a theoretical and computational study. Math. Program. 99, 563–591 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  47. Tawarmalani, M., Sahinidis, N.V.: A polyhedral branch-and-cut approach to global optimization. Math. Program. 103, 225–249 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  48. Vigerske, S.: Decomposition in multistage stochastic programming and a constraint integer programming approach to mixed-integer nonlinear programming. PhD thesis, Humboldt-Universität zu, Berlin (2012)

  49. Wächter, A., Biegler, L.T.: On the implementation of a primal-dual interior point filter line search algorithm for large-scale nonlinear programming. Math. Program. 106, 25–57 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  50. Westerlund, T., Pörn, R.: Solving pseudo-convex mixed integer optimization problems by cutting plane techniques. Optim. Eng. 3, 253–280 (2002)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA, USA

    Aida Khajavirad & Nikolaos V. Sahinidis

Authors
  1. Aida Khajavirad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nikolaos V. Sahinidis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nikolaos V. Sahinidis.

Additional information

This research was supported in part by National Science Foundation Award CMII-1030168.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khajavirad, A., Sahinidis, N.V. A hybrid LP/NLP paradigm for global optimization relaxations. Math. Prog. Comp. 10, 383–421 (2018). https://doi.org/10.1007/s12532-018-0138-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12532-018-0138-5

Keywords

Mathematics Subject Classification

Search

Navigation