Skip to main content
Springer Nature Link
Log in

Stochastic Hybrid System with Polynomial Growth Coefficients

  • Published:
Cognitive Computation Aims and scope Submit manuscript

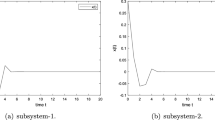
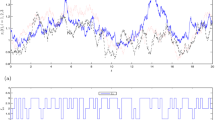
Abstract

The environmental and telegraph noise may be beneficial in the cognitive systems. In this paper, we will study a class of nonlinear system with Markovian switching, whose coefficients satisfy the one-sided polynomial growth condition and the local Lipschitz condition. This paper shows that the Brownian motion may suppress the potential explosion of the solution of the deterministic nonlinear system under some conditions. Moreover, another Brownian motion may exponentially stabilize the system. Finally, an example is given to illustrate our results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Indiveri G, Chicca E. Artificial cognitive systems: from VLSI networks of spiking neurons to neuromorphic cognition. Cogn Comput 2009;1:119–127.

    Article  Google Scholar 

  2. Seth A. Explanatory correlates of consciousness: theoretical and computational challenges. Cogn Comput 2009;1:50–63.

    Article  Google Scholar 

  3. Fellenz WA. Foveal attention and inhibition of return: a model for the generation of perceptual scan paths. Cogn Comput 2011;3:303–310.

    Article  Google Scholar 

  4. Zeng Z, Huang D, Wang Z. Pattern memory analysis base on stability theory of cellular neural networks. Appl Math Model 2008;32:112–121.

    Article  Google Scholar 

  5. Zeng Z, Wang J. Analysis and design of associative memories based on recurrent neural networks with linear saturation activation functions and time-varying delays. Neural Comput 2007;19:2149-2182.

    Article  PubMed  Google Scholar 

  6. Martin W, Florian E, Alex G et al. Bidirectional LSTM networks for contexensitive keyword detection in a cognitive virtual agent framework. Cogn Comput. 2010;2:180–190.

    Article  Google Scholar 

  7. Ron S, Nick W, Robert M. Accounting for certain mental disordes within a comprehensive cognitive architecture. Cogn Comput 2011;3:341–359.

    Article  Google Scholar 

  8. Gard TC. Stability for multispecies population models in random environments. Nonlinear Anal 1986;10:1411–1419.

    Article  Google Scholar 

  9. Mao X, Marion G, Renshaw E. Environmental Brownian noise suppresses explosions in population dynamics. Stoch Proc Appl 2002;97:95–110.

    Article  Google Scholar 

  10. Li X, Gray A, Jiang D, Mao X. Sufficient and necessary conditions of stochastic permanence and extinction for stochastic logistic populations under regime switching. J Math Anal Appl 2011;376:11–28.

    Article  Google Scholar 

  11. Mohammad MA, John MB, Suzanne C. Creativity and autonomy in swarm intelligence systems. Cong Comput 2012; to be published.

  12. Abdelhak B, Abdelhak B. Recognition of handwritten Arabic literal amounts using a hybrid approach. Cogn Comput. 2011;3:382–393.

    Article  Google Scholar 

  13. Athans M. Command and control (C2) theory: A challenge to control science, IEEE Trans Automat Contr 1987;32:286–293.

    Article  Google Scholar 

  14. Sworder DD, Rogers RO. An LQ-solution to a control problem associated with a solar thermal central receiver. IEEE Trans Automat Contr 1983;28:971–978.

    Article  Google Scholar 

  15. Kazangey T, Sworder DD. Effective federal policies for regulating residential housing. In: Proceedings of summer computer simulation conference, Sandiego; 1971. pp 1120–1128.

  16. Hasminskii RZ. Stochastic stability of differential equations. The Netherlands: Sijthoff and Noordhoof, Alphen aan den Rijin; 1981.

    Google Scholar 

  17. Zhu S, Shen Y, Chen GC. Noise suppress exponential growth for hybrid Hopfield neural networks. Math Comput Simul 2011;10:1016.

    Google Scholar 

  18. Mao X. Stochastic differential equations and applications. Chichester:Horwood; 1997.

    Google Scholar 

  19. Robinson JAD, Mao X. Stochastic stabilisation of functional differential equations. Syst Contr Lett 2005;54(11):1069–1081.

    Article  Google Scholar 

  20. Appleby JAD, Mao X, Rodkina A. On stochastic stabilization of differencee quations. Discrete Continuous Dyn Syst Ser A 2006;15(3):843–857.

    Article  Google Scholar 

  21. Appleby JAD, Mao X, Rodkina A. Stabilization and destabilization of nonlinear differential equations by noise. IEEE Trans Autom Contr 2008;53:683–691.

    Article  Google Scholar 

  22. Deng F, Luo Q, Mao X, Pang S. Noise supress or express exponential growth. Syst Cont Lett 2008;57:262–270.

    Article  Google Scholar 

  23. Wu F, Hu S. Suppression and stabilisation of noise. Int J Contr 2009;82:2150–2157.

    Article  Google Scholar 

  24. Mao X. Exponential stability of stochastic differential equations. NewYork: Dekker; 1994.

    Google Scholar 

Download references

Acknowledgments

The work is supported by the Fundamental Research Funds for the Central Universities under Grant 2012089, Zhongnan University of Economics and Law and China Postdoctoral Science Foundation funded project under Grant 2012M511615.

Author information

Authors and Affiliations

  1. Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan, 430074, China

    Lizhu Feng

  2. School of Mathematics and Computer Science, Jianghan University, Wuhan, 430056, China

    Lizhu Feng

  3. School of Statistics and Mathematics, Zhongnan University of Economics and Law, Wuhan, 430073, China

    Feng Jiang

  4. School of Measuring and Optoelectronic Engineering, Nanchang Hangkong University, Nanchang, Jiangxi, 330063, China

    Feng Li

Authors
  1. Lizhu Feng
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Feng Jiang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Feng Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Lizhu Feng.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Feng, L., Jiang, F. & Li, F. Stochastic Hybrid System with Polynomial Growth Coefficients. Cogn Comput 5, 32–39 (2013). https://doi.org/10.1007/s12559-012-9149-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12559-012-9149-0

Keywords