Skip to main content
Springer Nature Link
Log in

Improved Jacobian Eigen-Analysis Scheme for Accelerating Learning in Feedforward Neural Networks

  • Published:
Cognitive Computation Aims and scope Submit manuscript

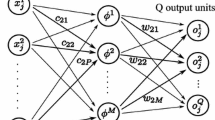
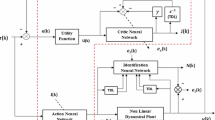
Abstract

An important problem in the learning process when training feedforward artificial neural networks is the occurrence of temporary minima which considerably slows down learning convergence. In a series of previous works, we analyzed this problem by deriving a dynamical system model which is valid in the vicinity of temporary minima caused by redundancy of nodes in the hidden layer. We also demonstrated how to incorporate the characteristics of the dynamical model into a constrained optimization algorithm that allows prompt abandonment of temporary minima and acceleration of learning. In this work, we revisit the constrained optimization framework in order to develop a closed-form solution for the evolution of critical dynamical system model parameters during learning in the vicinity of temporary minima. We show that this formalism is equivalent to matrix perturbation theory which was discussed in a previous work, but that the closed-form solution presented in the present paper allows for a weight update rule which is linear to the number of the network’s weights. In terms of computational complexity, this is equivalent to that of the simple back-propagation weight update rule. Simulations demonstrate the computational efficiency and effectiveness of this approach in reducing the time spent in the vicinity of temporary minima as suggested by the analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Amari S. Differential-geometrical method in statistics. Berlin: Springer; 1985.

    Book  Google Scholar 

  2. Amari S. Natural gradient works efficiently in learning. Neural Comput. 1998;10:251–76.

    Article  Google Scholar 

  3. Amari S, Park H, Fukumizu K. Adaptive method of realizing natural gradient learning for multilayer perceptrons. Neural Comput. 1999;12:1399–409.

    Article  Google Scholar 

  4. Amari S, Nagaoka H. Methods of information geometry. Providence, RI: American Mathematical Society; 2000.

    Google Scholar 

  5. Ampazis N, Perantonis S, Taylor J. Acceleration of learning in feedforward networks using dynamical systems analysis and matrix perturbation theory. In: International joint conference on neural networks. vol. 3. 1999. p. 1850–1855.

  6. Ampazis N, Perantonis S, Taylor J. Dynamics of multilayer networks in the vicinity of temporary minima. Neural Netw. 1999;12:43–58.

    Article  PubMed  Google Scholar 

  7. Ampazis N, Perantonis SJ, Taylor JG. A dynamical model for the analysis and acceleration of learning in feedforward networks. Neural Netw. 2001;14:1075–88.

    Article  CAS  PubMed  Google Scholar 

  8. Beer RD. Dynamical approaches to cognitive science. Trends Cogn Sci. 2000;4:91–9.

    Article  PubMed  Google Scholar 

  9. Bishop CM. Neural networks for pattern recognition. Oxford: Oxford University Press; 1996.

    Google Scholar 

  10. Botvinick M. Commentary: why i am not a dynamicist. Top Cogn Sci. 2012;4:78–83.

    Article  PubMed  Google Scholar 

  11. Boyce WE, DiPrima RC. Elementary differential equations and boundary value problems. London: Wiley; 1986.

    Google Scholar 

  12. Coddington EA, Levinson N. Theory of ordinary differential equations. New York: McGraw-Hill; 1955.

    Google Scholar 

  13. Fahlman SE. Faster learning variations on back propagation: an empirical study. In: Proceedings of the 1988 connectionist models summer school. 1988. p. 38–51.

  14. Fusella PV. Dynamic systems theory in cognitive science: major elements, applications, and debates surrounding a revolutionary meta-theory. Dyn Psychol. 2012–13. http://wp.dynapsyc.org/

  15. Gelder TV. The dynamical hypothesis in cognitive science. Behav Brain Sci. 1997;21:615–65.

    Google Scholar 

  16. Guo H, Gelfand SB. Analysis of gradient descent learning algorithms for multilayer feedforward networks. IEEE Trans Circuits Syst. 1991;38:883–94.

    Article  Google Scholar 

  17. Gros C. Cognitive computation with autonomously active neural networks: an emerging field. Cogn Comput. 2009;1(1):77–90.

    Article  Google Scholar 

  18. Heskes T. On “Natural” learning and pruning in multilayered perceptrons. Neural Comput. 2000;12:881–901.

    Article  CAS  PubMed  Google Scholar 

  19. Jacobs RA. Increased rates of convergence through learning rate adaptation. Neural Netw. 1988;1:295–307.

    Article  Google Scholar 

  20. Liang P. Design artificial neural networks based on the principle of divide-and-conquer. In: Proceedings of international conference on circuits and systems. 1991. p. 1319–1322.

  21. Murray AF. Analog VLSI and multi-layer perceptrons—accuracy, noise, and on-chip learning. In: Proceedings of second international conference on microelectronics for neural networks. 1991. p. 27–34.

  22. Parker D. Learning logic: casting the cortex of the human brain in silicon. Technical report TR-47 Invention Report 581–64, Center for Computational Research in Economics and Management Science, MIT. 1985.

  23. Perantonis SJ, Karras DA. An efficient constrained learning algorithm with momentum acceleration. Neural Netw. 1995;8:237–9.

    Article  Google Scholar 

  24. Riedmiller M, Braun H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In: Proceedings of the international joint conference on neural networks. 1993;1:586–91.

  25. Roth I, Margaliot M. Analysis of artificial neural network learning near temporary minima: a fuzzy logic approach. Fuzzy Sets Syst. 2010;161:2569–84.

    Article  Google Scholar 

  26. Shapiro LA. Dynamics and cognition. Minds Mach. 2013;23:353–75.

    Article  Google Scholar 

  27. Schöner G. Dynamical systems approaches to cognition. In: Cambridge handbook of computational cognitive modeling. Cambridge: Cambridge University Press; 2007.

  28. Seth A. Explanatory correlates of consciousness: theoretical and computational challenges. Cogn Comput. 2009;1(1):50–63.

    Article  Google Scholar 

  29. Spivey MJ. The continuity of mind. Oxford: Oxford University Press; 2007.

    Google Scholar 

  30. Sussmann HJ. Uniqueness of the weights for minimal feedforward nets with a given input–output map. Neural Netw. 1992;5:589–93.

    Article  Google Scholar 

  31. Trefethen LN, Bau D. Numerical linear algebra. USA: Society for Industrial and Applied Mathematics; 1997.

  32. Tyukin I, van Leeuwen C, Prokhorov D. Parameter estimation of sigmoid superpositions: dynamical system approach. Neural Comput. 2003;15:2419–55.

    Article  PubMed  Google Scholar 

  33. Woods D. Back and counter propagation abbreviations. In: Proceedings of the IEEE international conference on neural networks. 1988.

  34. Yang HH, Amari S. Complexity issues in natural gradient descent method for training multilayer perceptrons. Neural Comput. 1998;10:2137–57.

    Article  CAS  PubMed  Google Scholar 

  35. Zweiri YH. Optimization of a three-term backpropagation algorithm used for neural network learning. Int J Comput Intell. 2006;3(4):322–7.

Download references

Acknowledgments

Nicholas Ampazis would like to express his gratitude to his supervisor late Professor John G. Taylor for the guidance, patience, and continuous encouragement. John has been a source of inspiration to everyone that had the privilege to meet him and has left a shining imprint on the scientific community.

Author information

Authors and Affiliations

  1. Department of Financial and Management Engineering, University of the Aegean, 82100, Chios, Greece

    N. Ampazis & D. Drivaliaris

  2. Institute of Informatics and Telecommunications, National Center for Scientific Research “Demokritos”, Athens, Greece

    S. J. Perantonis

Authors
  1. N. Ampazis
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. J. Perantonis
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. D. Drivaliaris
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to N. Ampazis.

Appendix

Appendix

Let

$$\begin{aligned} {{\varvec{J}}}&= \sum _p(d^{(p)}-y^{(p)})y^{(p)}(1-y^{(p)})f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})(1-f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))\\&\quad \left( \begin{array}{cc} (1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})){\varvec{x^{(p)}}}({\varvec{x^{(p)}}})^{T}\nu &{} {\varvec{x^{(p)}}} \\ ({\varvec{x^{(p)}}})^{T} &{} 0\end{array}\right) \end{aligned}$$

with

$$\begin{aligned} y^{(p)}=f(b+K\nu f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})) \end{aligned}$$

and

$$\begin{aligned} {{\varvec{x^{(p)}}}}=\left( \begin{array}{c} x_1^{(p)}\\ x_2^{(p)}\\ \vdots \\ x_N^{(p)} \end{array} \right) \end{aligned}$$

If we let

$$\begin{aligned} A^{(p)}=(d^{(p)}-y^{(p)})y^{(p)}(1-y^{(p)})f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})(1-f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})) \end{aligned}$$

and

$$\begin{aligned} \lambda ^{(p)}=(1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))\nu \end{aligned}$$

then, we can write

$$\begin{aligned} {{\varvec{J}}}&= \sum _pA^{(p)}\left( \begin{array}{ccc} \left( \lambda ^{(p)} x_i^{(p)}x_j^{(p)}\right) _{1\le i,j\le N}&{}&{}{{\varvec{x^{(p)}}}}\\ &{}&{}\\ ({\varvec{x^{(p)}}})^{T}&{}&{}0 \end{array} \right) \end{aligned}$$

Let

$$\begin{aligned} {{\varvec{u}}}=\left( \begin{array}{c} u_1\\ u_2\\ \vdots \\ u_N\\ u_{N+1} \end{array} \right) \end{aligned}$$

A simple calculation shows that

$$\begin{aligned} {{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}}&= \displaystyle {\sum _p\left( \sum _{i=1}^Nu_ix_i^{(p)}\right) A^{(p)}\left( \lambda ^{(p)}\left( \sum _{j=1}^Nu_jx_j^{(p)}\right) +2u_{N+1}\right) } \nonumber \\ &= \displaystyle {\sum _p \left({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})A^{(p)}(\lambda ^{(p)}({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})+2u_{N+1}\right)} \end{aligned}$$
(43)

where

$$\begin{aligned} {{\tilde{\varvec{x}^{(p)}}}}=\left( \begin{array}{c} x_1^{(p)}\\ x_2^{(p)}\\ \vdots \\ x_N^{(p)}\\ 0 \end{array} \right) \end{aligned}$$

We want to calculate

$$\begin{aligned} \frac{\partial }{\partial \nu }({{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}})\quad \hbox { and }\quad \frac{\partial }{\partial {\varvec{\omega }}}({{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}}) \end{aligned}$$

Recall that

$$\begin{aligned} \frac{\text{d}f}{\text{d}t}(t)=f(t)(1-f(t))=f(t)-f^2(t) \end{aligned}$$
(44)

Using simple properties of the derivatives and (44), we get that

$$\begin{aligned} \frac{\partial y^{(p)}}{\partial \nu }=K(y^{(p)}-(y^{(p)})^2)f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}) \end{aligned}$$

which, using again simple properties of the derivatives, gives

$$\begin{aligned}&\displaystyle {\frac{\partial }{\partial \nu }}\left(d^{(p)}y^{(p)}-(1+d^{(p)})(y^{(p)}\right)^2+(y^{(p)})^3)\nonumber \\ &\quad = K\left(d^{(p)}-2(1+d^{(p)})y^{(p)} +3(y^{(p)})^2\right)\left(y^{(p)}-(y^{(p)}\right)^2)f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}) \end{aligned}$$

which implies that

$$\begin{aligned} \displaystyle {\frac{\partial A^{(p)}}{\partial \nu }}&= K \left(d^{(p)}-2(1+d^{(p)})y^{(p)}+3(y^{(p)})^2\right)\left(y^{(p)}-(y^{(p)})^2\right)\nonumber \\ &\quad f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})) \end{aligned}$$
(45)

On the other hand, we obviously have that

$$\begin{aligned} \frac{\partial \lambda ^{(p)}}{\partial \nu } =1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}) \end{aligned}$$
(46)

Using (45) and (46) and simple properties of the derivatives, we get that

$$\begin{aligned} \displaystyle {\frac{\partial }{\partial \nu }({{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}})}&= \displaystyle {\sum _p} \left({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})(y^{(p)}-(y^{(p)}\right)^2(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))\nonumber \\&\qquad ((d^{(p)}-y^{(p)})(1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})\nonumber \\&\quad +K(d^{(p)}-2(1+d^{(p)})y^{(p)}+3(y^{(p)})^2)f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})\nonumber \\&\qquad (\nu (1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})+2u_{N+1})) \end{aligned}$$
(47)

Let

$$\begin{aligned} \delta ^{(p)}&= (y^{(p)}-(y^{(p)})^2)(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))\end{aligned}$$
(48)
$$\begin{aligned} \rho ^{(p)}&= K (d^{(p)}-2(1+d^{(p)})y^{(p)}+3(y^{(p)})^2)f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})\nonumber \\&\quad (\nu (1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})+2u_{N+1}) \end{aligned}$$
(49)

Combining (47), (48), and (49), we get that

$$\begin{aligned}&\displaystyle {\frac{\partial }{\partial \nu }({{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}})}= \displaystyle {\sum _p}({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})\delta ^{(p)}\nonumber \\&\quad ((d^{(p)}-y^{(p)})(1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})+\rho ^{(p)}) \end{aligned}$$
(50)

For the evaluation of \(\frac{\partial }{\partial {\varvec{\omega }}}({{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}})\) , we have:

Using simple properties of the derivatives and (44), we get that

$$\begin{aligned} \frac{\partial f}{\partial {\varvec{\omega }}}({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})=(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})){{\varvec{x^{(p)}}}} \end{aligned}$$
(51)

which, using again simple properties of the derivatives and (44), gives

$$\begin{aligned} \frac{\partial y^{(p)}}{\partial {\varvec{\omega }}}=K\nu (y^{(p)}-(y^{(p)})^2)(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})){{\varvec{x^{(p)}}}} \end{aligned}$$

which implies that

$$\begin{aligned}&\displaystyle {\frac{\partial }{\partial {\varvec{\omega }}}}(d^{(p)}y^{(p)}-(1+d^{(p)})(y^{(p)})^2+(y^{(p)})^3)\nonumber \\&\quad = K\nu (d^{(p)}-2(1+d^{(p)})y^{(p)}+3(y^{(p)})^2) (y^{(p)}\nonumber \\&\qquad -(y^{(p)})^2)(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})){{\varvec{x^{(p)}}}} \end{aligned}$$
(52)

Using simple properties of the derivatives and (51), we get that

$$\begin{aligned} \displaystyle {\frac{\partial }{\partial {\varvec{\omega }}}}(f({{\varvec{\omega }}} \cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))&= (1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})\nonumber \\&\quad -f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})){{\varvec{x^{(p)}}}} \end{aligned}$$
(53)

Using simple properties of the derivatives and (52) and (53), we get that

$$\begin{aligned}\displaystyle {\frac{\partial A^{(p)}}{\partial {\varvec{\omega }}}}&=(y^{(p)}-(y^{(p)})^2)(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))((d^{(p)}-y^{(p)})(1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))\nonumber \\&\quad +K\nu (d^{(p)}-2(1+d^{(p)})y^{(p)}+3(y^{(p)})^2)(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))){{\varvec{x^{(p)}}}} \end{aligned}$$
(54)

On the other hand, using simple properties of the derivatives and (51), we get that

$$\begin{aligned} \frac{\partial \lambda ^{(p)}}{\partial {\varvec{\omega }}} =-2\nu (f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})){{\varvec{x^{(p)}}}} \end{aligned}$$
(55)

Using (54) and (55) and simple properties of the derivatives, we get that

$$\begin{aligned} \displaystyle {\frac{\partial }{\partial {\varvec{\omega }}}({{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}})}&= \displaystyle {\sum _p}({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})(y^{(p)}-(y^{(p)})^2)(f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})-f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))\nonumber \\&\quad (K(d^{(p)}-2(1+d^{(p)})y^{(p)}+3(y^{(p)})^2)f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})\nonumber \\&\quad (\nu (1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})+2u_{N+1}) \nu (1-f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))\nonumber \\&\quad +(d^{(p)}-y^{(p)}) (\nu (1-6f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})+6f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})\nonumber \\&\quad +2(1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))u_{N+1})){{\varvec{x^{(p)}}}} \end{aligned}$$
(56)

Combining (48), (49) and (56), we get that

$$\begin{aligned} \displaystyle {\frac{\partial }{\partial {\varvec{\omega }}}({{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}})}&= \displaystyle {\sum _p}({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})\delta ^{(p)}(\rho ^{(p)}\nu (1-f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))\nonumber \\&\quad +(d^{(p)}-y^{(p)}) (\nu (1-6f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}})+6f^2({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))({{\varvec{u}}}^T\cdot {{\tilde{\varvec{x}^{(p)}}}})\nonumber \\&\quad +2(1-2f({{\varvec{\omega }}}\cdot {{\varvec{x^{(p)}}}}))u_{N+1})){{\varvec{x^{(p)}}}} \end{aligned}$$
(57)

For a Jacobian matrix of size \(Q \times Q\), it follows that there are Q derivatives to evaluate. By simply taking the expression for the differential of Eq. (27) and evaluating it at small perturbations by finite differences, we would have to evaluate Q such terms (one for each component of the state vector \({{\varvec{\varOmega }}}\)), each requiring O(Q) operations. Thus, the total computational effort required to evaluate all the derivatives scales as \(O(Q^2)\).

Equations (50) and (57) allow the derivatives to be propagated back and evaluated in O(Q) operations similarly to the back-propagation algorithm which requires O(W) operations, where W is the number of the network’s weights [9]. This follows from the fact that both the forward phase [evaluation of Eq. (43)] and the backward propagation phases are O(Q), and the evaluation of the derivatives require O(Q) operations. Thus the closed-form solution has reduced the computational complexity from \(O(Q^2)\) of the finite differences method to O(Q) for each input vector, which results in a significant computational gain.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ampazis, N., Perantonis, S.J. & Drivaliaris, D. Improved Jacobian Eigen-Analysis Scheme for Accelerating Learning in Feedforward Neural Networks. Cogn Comput 7, 86–102 (2015). https://doi.org/10.1007/s12559-014-9263-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12559-014-9263-2

Keywords