Skip to main content
SpringerLink
Log in

A New Risk-Based Fuzzy Cognitive Model and Its Application to Decision-Making

  • Published:
Cognitive Computation Aims and scope Submit manuscript

Abstract

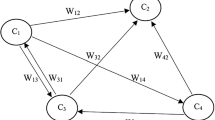
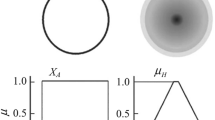
Cognitive information in real-world decision-making problems is usually associated with all sorts of ambiguities and uncertainties. Fuzzy sets have been proposed as a general workaround for such information representation. Notwithstanding, there are cases in which the fuzzy sets and fuzzy numbers have some degree of uncertainty when available data either come from unreliable sources or refer to events in the future. These situations result in some unreliability of the obtained fuzzy information. For the modeling of the possible future-event effects on the fuzzy information credibility, the present research presents a novel risk-based fuzzy cognitive methodology by investigating all possible cases to risk modeling of fuzzy sets and the governing mathematical equations. The new fuzzy cognitive model is used to develop a multi-criteria decision-making method based on a fuzzy TOPSIS method so-called RFC-TOPSIS, and the proposed approach was tested on a case study of failure modes and effects analysis problem. Based on the results, robust outcomes were obtained when the proposed methodology was used, highlighting the flexibility and the efficiency of the proposed methodology. The present concept can be used to deal with any problems, where membership function is associated with some risks and errors due to risk factors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Sun G, Guan X, Yi X, Zhou Z. Improvements on correlation coefficients of hesitant fuzzy sets and their applications. Cogn Comput. 2019;11(4):529–44 1-16.

    Google Scholar 

  2. Liu P, Zhang X. A novel picture fuzzy linguistic aggregation operator and its application to group decision-making. Cogn Comput. 2018;10(2):242–59.

    Google Scholar 

  3. Tao Z, Han B, Chen H. On intuitionistic fuzzy copula aggregation operators in multiple-attribute decision making. Cogn Comput. 2018;10(4):610–24.

    Google Scholar 

  4. Ma Z, Zhu J, Ponnambalam K, Chen Y, Zhang S. Group decision-making with linguistic cognition from a reliability perspective. Cogn Comput. 2019;11(2):172–92 1-21.

    Google Scholar 

  5. Wang JQ, Cao YX, Zhang HY. Multi-criteria decision-making method based on distance measure and choquet integral for linguistic Z-numbers. Cogn Comput. 2017;9(6):827–42.

    Google Scholar 

  6. Ye J. Multiple attribute decision-making methods based on the expected value and the similarity measure of hesitant neutrosophic linguistic numbers. Cogn Comput. 2018;10(3):454–63.

    Google Scholar 

  7. Turksen IB. Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986;20(2):191–210.

    Google Scholar 

  8. Atanassov KT (2012) On intuitionistic fuzzy sets theory (Vol. 283). Springer.

  9. Atanassov K, Gargov G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989;31(3):343–9.

    Google Scholar 

  10. Xiao F, Ding W. Divergence measure of Pythagorean fuzzy sets and its application in medical diagnosis. Appl Soft Comput. 2019.

  11. Zhai Y, Xu Z, Liao H. Measures of probabilistic interval-valued intuitionistic hesitant fuzzy sets and the application in reducing excessive medical examinations. IEEE Trans Fuzzy Syst. 2017;26(3):1651–70.

    Google Scholar 

  12. Zadeh LA. A note on Z-numbers. Inf Sci. 2011;181(14):2923–32.

    Google Scholar 

  13. Rodríguez RM, Bedregal B, Bustince H, Dong YC, Farhadinia B, Kahraman C, et al. A position and perspective analysis of hesitant fuzzy sets on information fusion in decision making. Towards high quality progress. Information Fusion. 2016;29:89–97.

    Google Scholar 

  14. Ji P, Zhang HY, Wang JQ. A projection-based outranking method with multi-hesitant fuzzy linguistic term sets for hotel location selection. Cogn Comput. 2018;10:737–51.

    Google Scholar 

  15. Zhu B, Xu Z, Xia M. Dual hesitant fuzzy sets. J Appl Math. 2012;2012:13.

    Google Scholar 

  16. Farhadinia B. Information measures for hesitant fuzzy sets and interval-valued hesitant fuzzy sets. Inf Sci. 2013;240:129–44.

    Google Scholar 

  17. Pang Q, Wang H, Xu Z. Probabilistic linguistic term sets in multi-attribute group decision making. Inf Sci. 2016;369:128–43.

    Google Scholar 

  18. Ye J. Similarity measures between interval neutrosophic sets and their applications in multicriteria decision-making. J Intell Fuzzy Syst. 2014;26(1):165–72.

    Google Scholar 

  19. Şahin R, Liu P. The correlation coefficient of single-valued neutrosophic hesitant fuzzy sets and its applications in decision making. Neural Comput & Applic. 2017;28(6):1387–95.

    Google Scholar 

  20. Song W, Zhu J. A multistage risk decision making method for normal cloud model considering behavior characteristics. Appl Soft Comput. 2019;78:393–406.

    Google Scholar 

  21. Smarandache F. Plithogenic set, an extension of crisp, fuzzy, intuitionistic fuzzy, and neutrosophic sets–revisited. Neutrosophic Sets and Systems. 2018;21:153–66.

    Google Scholar 

  22. Cuong, B. C., & Kreinovich, V. (2013). Picture Fuzzy Sets-a new concept for computational intelligence problems. In Information and Communication Technologies (WICT), 2013 Third World Congress on (pp. 1-6). IEEE.

  23. Xiao F. A novel multi-criteria decision making method for assessing health-care waste treatment technologies based on D numbers. Eng Appl Artif Intell. 2018;71:216–25.

    Google Scholar 

  24. Li X, Chen X. D-intuitionistic hesitant fuzzy sets and their application in multiple attribute decision making. Cogn Comput. 2018;10(3):496–505.

    Google Scholar 

  25. Seiti H, Hafezalkotob A, Martínez L. R-numbers, a new risk modeling associated with fuzzy numbers and its application to decision making. Inf Sci. 2019;483:206–31.

    Google Scholar 

  26. Seiti H, Hafezalkotob A, Fattahi R. Extending a pessimistic–optimistic fuzzy information axiom based approach considering acceptable risk: application in the selection of maintenance strategy. Appl Soft Comput. 2018;67:895–909.

    Google Scholar 

  27. Seiti H, Tagipour R, Hafezalkotob A, Asgari F. Maintenance strategy selection with risky evaluations using RAHP. J Multi-Criteria Decis Anal. 2017;24(5-6):257–74.

    Google Scholar 

  28. Seiti H, Hafezalkotob A, Najafi SE, Khalaj M. A risk-based fuzzy evidential framework for FMEA analysis under uncertainty: an interval-valued DS approach. J Intell Fuzzy Syst. 2018;35(2):1419–30 (Preprint), 1-12.

    Google Scholar 

  29. Seiti H, Hafezalkotob A. Developing pessimistic–optimistic risk-based methods for multi-sensor fusion: an interval-valued evidence theory approach. Appl Soft Comput. 2018;72:609–23.

    Google Scholar 

  30. Gören HG, Kulak O. A new fuzzy multi-criteria decision making approach: extended hierarchical fuzzy axiomatic design approach with risk factors. In: Decision Support Systems III-Impact of Decision Support Systems for Global Environments. Cham: Springer; 2014. p. 141–56.

    Google Scholar 

  31. Kulak O, Goren HG, Supciller AA. A new multi criteria decision making approach for medical imaging systems considering risk factors. Appl Soft Comput. 2015;35:931–41.

    Google Scholar 

  32. Hafezalkotob A, Hafezalkotob A. Risk-based material selection process supported on information theory: a case study on industrial gas turbine. Appl Soft Comput. 2017;52:1116–29.

    Google Scholar 

  33. Ijadi Maghsoodi A, Hafezalkotob A, Azizi Ari I, Ijadi Maghsoodi S, Hafezalkotob A. Selection of waste lubricant oil regenerative technology using entropy-weighted risk-based fuzzy axiomatic design approach. Informatica. 2018;29(1):41–74.

    Google Scholar 

  34. Seiti H, Hafezalkotob A. Developing the R-TOPSIS methodology for risk-based preventive maintenance planning: a case study in rolling mill company. Comput Ind Eng. 2019;128:622–36.

    Google Scholar 

  35. Bede B. Mathematics of fuzzy sets and fuzzy logic. Berlin, Heidelberg: Springer-Verlag; 2013.

    Google Scholar 

  36. Shokeen J, & Rana C (2017). Fuzzy sets, advanced fuzzy sets and hybrids. In 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS) (pp. 2538-2542). IEEE.

  37. Fuchs E, & Masoum MA (2011). Power quality in power systems and electrical machines. Academic press.

  38. Patel AV, Mohan BM. Some numerical aspects of center of area defuzzification method. Fuzzy Sets Syst. 2002;132(3):401–9.

    Google Scholar 

  39. Van Broekhoven E, De Baets B. Fast and accurate center of gravity defuzzification of fuzzy system outputs defined on trapezoidal fuzzy partitions. Fuzzy Sets Syst. 2006;157(7):904–18.

    Google Scholar 

  40. Jiang W, Luo Y, Qin XY, Zhan J. An improved method to rank generalized fuzzy numbers with different left heights and right heights. J Intell Fuzzy Syst. 2015;28(5):2343–55.

    Google Scholar 

  41. Mendel JM, Rajati MR, Sussner P. On clarifying some definitions and notations used for type-2 fuzzy sets as well as some recommended changes. Inf Sci. 2016;340:337–45.

    Google Scholar 

  42. Kahraman C, Öztayşi B, Sarı İU, Turanoğlu E. Fuzzy analytic hierarchy process with interval type-2 fuzzy sets. Knowl-Based Syst. 2014;59:48–57.

    Google Scholar 

  43. Joshi D, Kumar S. Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. Eur J Oper Res. 2016;248(1):183–91.

    Google Scholar 

  44. Zhang X, Xu Z. Soft computing based on maximizing consensus and fuzzy TOPSIS approach to interval-valued intuitionistic fuzzy group decision making. Appl Soft Comput. 2015;26:42–56.

    Google Scholar 

  45. Seiti HR, Behnampour A, Imani DM, Houshmand M. Failure modes and effects analysis under fuzzy environment using fuzzy axiomatic design approach. Int J Research Ind Eng. 2017;6(1):51–68.

    Google Scholar 

  46. Capuano N, Chiclana F, Fujita H, Herrera-Viedma E, Loia V. Fuzzy group decision making with incomplete information guided by social influence. IEEE Trans Fuzzy Syst. 2018;26(3):1704–18.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran

    Hamidreza Seiti

  2. Department of Industrial Engineering, Islamic Azad University, South Tehran Branch, Tehran, Iran

    Ashkan Hafezalkotob

Authors
  1. Hamidreza Seiti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ashkan Hafezalkotob
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hamidreza Seiti.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

  • Example 1. Letting the risks associated with membership function and set elements of a reference set X and the fuzzy set \( \tilde{A} \) as rμ− = 0.3 and rx− = 0.2,respectively, the pessimistic set \( {\tilde{A}}_{Pb} \) can be obtained as follows.

$$ {\displaystyle \begin{array}{l}X=\left\{1,2,3,4\right\}\\ {}A=\left\{\left(1,0.2\right),\left(2,0.4\right),\left(3,0.5\right),\left(4,0.7\right)\right\}\\ {}{\tilde{A}}_P=\left\{\left(1,\left[0.14,0.2\right]\right),\left(2,\left[0.28,0.4\right]\right),\left(3,\left[0.35,0.5\right]\right),\left(4,\left[0.49,0.7\right]\right)\right\}\end{array}} $$

  • Example 2. Taking the X and fuzzy set \( \tilde{A} \) of Example 1 and assuming the risks of membership function as r− = 0.3 and r+ = 0.2, the pessimistic-optimistic set \( {\tilde{A}}_{P- OT}(x) \) can be written as follows.

$$ {\displaystyle \begin{array}{l}X=\left\{1,2,3,4\right\}\\ {}\tilde{A}=\left\{\left(1,0.2\right),\left(2,0.4\right),\left(3,0.5\right),\left(4,0.7\right)\right\}\\ {}{\tilde{\tilde{A}}}_{P- OT}(x)=\left\{\left(1,\left(0.14,0.2,0.24\right)\right),\left(2,\left(0.28,0.4,0.48\right)\right),\left(3,\left(0.35,0.5,0.6\right)\right),\left(4,\left(0.49,0.7,0.84\right)\right)\right\}\end{array}} $$

  • Example 3. Suppose GTrFN \( \tilde{A}=\left(1,2,3,4;\mathrm{0.4,0.6}\right) \) and rL− = 0.2, rR− = 0.3, rL+ = 0.3 and rR+ = 0.2 , \( {\tilde{\tilde{A}}}^{P- OT} \) is determined as follows:

$$ {\displaystyle \begin{array}{l}\tilde{A}=\left(1,2,3,4;0.4,0.6\right),\kern0.33em {r_L}^{-}=0.2,{r_R}^{-}=0.3,{r_L}^{+}=0.3\kern0.66em {r_R}^{+}=0.2\\ {}{\tilde{\tilde{A}}}^{P- OT}=\left(\left(1,2,3,4;0.32,0.42\right),\left(1,2,3,4;0.4,0.6\right),\left(1,2,3,4;0.52,0.72\right)\right)\end{array}} $$

  • Example 4. By letting ={1}, A = {(1,0.2)}, B = {(1,0.5)}, RA = {0.3, 0.4, 0.2, 0.1}, and RB = {0.2, 0.1, 0.2, 0.1},then we have

$$ {\displaystyle \begin{array}{l}A=\left\{\left(1,0.2\right)\right\},\kern0.33em {r}_A^{-}=0.3,{r}_A^{+}=0.3,A{R_A}^{-}=0.2\kern0.33em and\kern0.58em A{R}_A^{+}=0.1\kern0.33em \to RF{C}_A(x)=\left\{\left(1,\left(0.152,0.2,0.254\right)\right)\right\}\\ {}B=\left(1,0.5\right),\kern0.33em {r}_B^{-}=0.2,\kern0.33em ?{r}_B^{+}=0.1,A{R}_B^{-}=0.2\kern0.33em and\kern0.33em A{R}_A^{+}=0.1\kern0.33em \to RF{C}_B(x)=\left(1,\left(0.42,0.5,0.545\right)\right)\end{array}} $$
$$ {\displaystyle \begin{array}{l}\ {\mathrm{RFC}}_A(x)\cup {\mathrm{RFC}}_B(x)=\left\{\left(1,\left(0.42,0.5,0.545\right)\right)\right\}\\ {}\ {\mathrm{RFC}}_A(x)\cap {\mathrm{RFC}}_B(x)=\left\{\left(1,\left(0.152,0.2,0.254\right)\right)\right\}\\ {}\ {\mathrm{RFC}}_A(x)\oplus {\mathrm{RFC}}_B(x)=\left\{\left(1,\left(0.5082,0.6,0.6606\right)\right)\right\}\\ {}\ {\mathrm{RFC}}_A(x)\otimes {\mathrm{RFC}}_B(x)=\left\{\left(1,\left(0.0638,0.1,0.13843\right)\right)\right\}\end{array}} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Seiti, H., Hafezalkotob, A. A New Risk-Based Fuzzy Cognitive Model and Its Application to Decision-Making. Cogn Comput 12, 309–326 (2020). https://doi.org/10.1007/s12559-019-09701-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12559-019-09701-8

Keywords

Search

Navigation