Skip to main content
Springer Nature Link
Log in

Bifurcation Study for Fractional-Order Three-Layer Neural Networks Involving Four Time Delays

  • Published:
Cognitive Computation Aims and scope Submit manuscript

Abstract

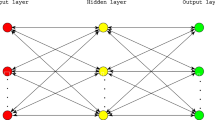
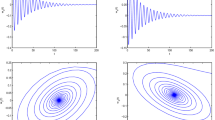
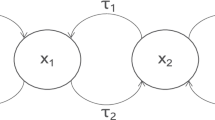
During the past several decades, many scholars deal with the stability behavior and Hopf bifurcation phenomenon of fractional-order delayed neural networks. However, the literature involving the stability issue and Hopf bifurcation behavior of fractional-order neural networks with multiple time delays is relatively scarce. This article is principally concerned with the stability problem and of Hopf bifurcation behavior of fractional-order three-layer neural networks involving multiple time delays. Variable substitution, Laplace transform, bifurcation principle of fractional-order dynamical system and computer simulation skill are employed. The delay-independent stability criterion and the sufficient condition of onset of Hopf bifurcation of three-layer neural networks are set up. It shows that if the sum of both different delays passes a key value, then the system loses its stability and the Hopf bifurcation phenomenon will take place. The study manifests that delay plays a most momentous part in stabilizing system and controlling bifurcation behavior for the fractional-order delayed three-layer neural networks. The researchful results of this article are an important theoretical cornerstone in controlling and adjusting neural networks. The obtained conclusions are completely novel and complement the earlier research results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figs. 1-20
Figs. 1-20
Figs. 1-20
Figs. 21-40
Figs. 21-40
Figs. 21-40
Figs. 41
Figs. 42
Figs. 43
Figs. 44
Figs. 45
Figs. 46

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Wang TY, Zhu QX. Stability analysis of stochastic BAM neural networks with reaction-diffusion, multi-proportional and distributed delays. Phys A: Stat Mech Appl. 2019;533:121935.

    Article  MathSciNet  Google Scholar 

  2. Sowmiya C, Raja R, Zhu QX, Rajchakit G. Further mean-square asymptotic stability of impulsive discrete-time stochastic BAM neural networks with Markovian jumping and multiple time-varying delays. J Franklin Inst. 2019;356(1):561–91.

    Article  MathSciNet  Google Scholar 

  3. Aouiti C, Gharbia IB, Cao JD, Alsaedi A. Dynamics of impulsive neutral-type BAM neural networks. J Franklin Inst. 2019;356(4):2294–324.

    Article  MathSciNet  Google Scholar 

  4. Aouiti C, Gharbia IB, Cao JD, Mhamdi MS, Alsaedi A. Existence and global exponential stability of pseudo almost periodic solution for neutral delay BAM neural networks with time-varying delay in leakage terms. Chaos Solitons Fractals. 2018;107:111–27.

    Article  MathSciNet  Google Scholar 

  5. Chen LP, Yin H, Huang TW, Yuan LG, Zheng S, Yin LS. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 2020;125:174–84.

    Article  Google Scholar 

  6. Wang P, Li XC, Wang N, Li YY, Shi KB, Lu JQ. Almost periodic synchronization of quaternion-valued fuzzy cellular neural networks with leakage delays. Fuzzy Set Syst. 2021. https://doi.org/10.1016/j.fss.2021.02.019.

  7. Békollè D, Ezzinbi K, Fatajou S, Houpa Danga DE, Béssémè FM. Attractiveness of pseudo almost periodic solutions for delayed cellular neural networks in the context of measure theory. Neurocomputing. 2021;435:253–63.

    Article  Google Scholar 

  8. Li YK, Shen SP. Almost automorphic solutions for Clifford-valued neutral-type fuzzy cellular neural networks with leakage delays on time scales. Neurocomputing. 2020;417:23–35.

    Article  Google Scholar 

  9. Xu CJ, Liao MX, Li PL, Liu ZX, Yuan S. New results on pseudo almost periodic solutions of quaternion-valued fuzzy cellular neural networks with delays. Fuzzy Set Syst. 2021;411:25–47.

    Article  Google Scholar 

  10. Liu YF, Song ZQ, Tan MC. Multiple \(\mu\)-stability and multiperiodicity of delayed memristor-based fuzzy cellular neural networks with nonmonotonic activation functions. Math Comput Simul. 2019;159:1–17.

  11. Xu CJ, Li PL. On anti-periodic solutions for neutral shunting inhibitory cellular neural networks with time-varying delays and D operator. Neurocomputing. 2018;275:377–82.

    Article  Google Scholar 

  12. Wang WT. Finite-time synchronization for a class of fuzzy cellular neural networks with time-varying coefficients and proportional delays. Fuzzy Set Syst. 2018;338:40–9.

    Article  MathSciNet  Google Scholar 

  13. Zheng MW, Li LX, Peng HP, Xiao JH, Yang YX, Zhang YP, Zhao H. Fixed-time synchronization of memristor-based fuzzy cellular neural network with time-varying delay. J Franklin Inst. 2018;355(14):6780–809.

    Article  MathSciNet  Google Scholar 

  14. Xu CJ, Tang XH, Liao MX. Stability and bifurcation analysis of a six-neuron BAM neural network model with discrete delays. Neurocomputing. 2011;74(5):689–707.

    Article  Google Scholar 

  15. Gopalsamy K, He X. Delay-independent stability in bidirectional associative memory networks. IEEE Trans Neural Netw. 1994;5(6):998–1002.

    Article  Google Scholar 

  16. Zhou QY. Convergence for a two-neuron network with delays. Appl Math Lett. 2009;22(8):1181–4.

    Article  MathSciNet  Google Scholar 

  17. Jiang FF, Shen JH, Li XD. The LMI method for stationary oscillation of interval neural networks with three neuron activations under impulsive effects. Nonlinear Anal: Real World Appl. 2013;14(3):1404–16.

    Article  MathSciNet  Google Scholar 

  18. Hu HJ, Huang LH. Stability and Hopf bifurcation analysis on a ring of four neurons with delays. Appl Math Comput. 2009;213(2):587–99.

    MathSciNet  MATH  Google Scholar 

  19. Ge JH, Xu J. Synchronization and synchronized periodic solution in a simplified five-neuron BAM neural network with delays. Neurocomputing. 2011;74(6):993–9.

    Article  Google Scholar 

  20. Xu CJ, Zhang QM. Bifurcation analysis of a tri-neuron neural network model in the frequency domain. Nonlinear Dyn. 2014;76(1):33–46.

    Article  MathSciNet  Google Scholar 

  21. Xu CJ, Liao MX, Li PL, Guo Y. Bifurcation analysis for simplified five-neuron bidirectional associative memory neural networks with four delays. Neural Process Lett. 2019;50(3):2219–45.

    Article  Google Scholar 

  22. Xu CJ, Tang XH, Liao MX. Frequency domain analysis for bifurcation in a simplified tri-neuron BAM network model with two delays. Neural Netw. 2010;23(7):872–80.

    Article  Google Scholar 

  23. Hajihosseini A, Maleki F, Rokni Lamooki GR. Bifurcation analysis on a generalized recurrent neural network with two interconnected three-neuron components. Chaos Solitons Fract. 2011;44(11):1004–19.

    Article  Google Scholar 

  24. Amin R, Shah K, Asif M, Khan I. A computational algorithm for the numerical solution of fractional order delay differential equations. Appl Math Comput. 2021;402:125863.

    MathSciNet  MATH  Google Scholar 

  25. Ammour AS, Djennoune S, Bettayeb M. A sliding mode control for linear fractional systems with input and state delays. Commun Nonlinear Sci Numer Simul. 2009;14:2310–8.

    Article  MathSciNet  Google Scholar 

  26. Zhang JM, Wu JW, Bao HB, Cao JD. Synchronization analysis of fractional-order three-neuron BAM neural networks with multiple time delays. Appl Math Comput. 2018;339:441–50.

    Article  MathSciNet  Google Scholar 

  27. Pratap A, Raja R, Cao JD, Rajchakit G, Alsaadi FES. Further synchronization in finite time analysis for time-varying delayed fractional order memristive competitive neural networks with leakage delay. Neurocomputing. 2018;317:110–26.

    Article  Google Scholar 

  28. Xu CJ, Liao MX, Li PL, Guo Y, Liu ZX. Bifurcation properties for fractional order delayed BAM neural networks. Cogn Comput. 2021;13(2):322–56.

    Article  Google Scholar 

  29. Xu CJ, Liu ZX, Liao MX, Li PL, Xiao QM, Yuan S. Fractional-order bidirectional associate memory (BAM) neural networks with multiple delays: The case of Hopf bifurcation. Math Comput Simul. 2021;182:471–94.

    Article  MathSciNet  Google Scholar 

  30. Huang CD, Wang J, Chen XP, Cao JD. Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw. 2021;141:344–54.

    Article  Google Scholar 

  31. Huang CD, Liu H, Shi XY, Chen XP, Xiao M, Wang ZX, Cao JD. Bifurcations in a fractional-order neural network with multiple leakage delays. Neural Netw. 2020;131:115–26.

    Article  Google Scholar 

  32. Cheng ZS, Li DH, Cao JD. Stability and Hopf bifurcation of a three-layer neural network model with delays. Neurocomputing. 2016;175:355–70.

    Article  Google Scholar 

  33. Podlubny I. Fractional Differential Equations. New York: Academic Press; 1999.

    MATH  Google Scholar 

  34. Matignon D. Stability results for fractional differential equations with applications to control processing. Comput Eng Syst Appl. 1996;2:963–8.

    Google Scholar 

  35. Deng WH, Li CP, Lü JH. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007;48(4):409–16.

    Article  MathSciNet  Google Scholar 

  36. Jia J, Huang X, Li YX, Cao JD, Alsaedi A. Global stabilization of fractional-order memristor-based neural networks with time delay. IEEE Trans Neural Netw Learning Syst. 2020;31(3):997–1009.

    Article  MathSciNet  Google Scholar 

  37. Wang Z, Wang XH, Xia JW, Shen H, Meng B. Adaptive sliding mode output tracking control based-FODOB for a class of uncertain fractional-order nonlinear time-delayed systems. SCI CHINA Tech Sci. 2020;63:1854–62.

    Article  Google Scholar 

  38. Hu C, He HB, Jiang HJ. Edge-based adaptive distributed method for synchronization of intermittently coupled spatiotemporal networks. IEEE Trans Auto Cont. 2021. https://doi.org/10.1109/TAC.2021.3088805.

  39. Hu C, Jiang HJ. Special functions-based fixed-time estimation and stabilization for dynamic systems. IEEE Trans Syst Man Cybern Syst. 2021;99:1–12.

  40. Zheng BB, Hu C, Yu J, Jiang HJ. Synchronization Analysis for delayed spatio-temporal neural networks with fractional-order. Neurocomputing. 2021;441:226–36.

    Article  Google Scholar 

  41. Wang HF, Xiao M, Tao BB, Xu FY, Wang ZX, Huang CD, Qiu JL. Improving dynamics of integer-order small-world network models under fractional-order PD control. Sci China Infor Sci. 2020;63:112206.

    Article  MathSciNet  Google Scholar 

Download references

Funding

The work is supported by National Natural Science Foundation of China (No.61673008 and No.62062018) and Project of High-level Innovative Talents of Guizhou Province ([2016]5651) and Major Research Project of The Innovation Group of The Education Department of Guizhou Province ([2017]039), Key Project of Hunan Education Department (17A181), Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering (Changsha University of Science & Technology)(2018MMAEZD21), University Science and Technology Top Talents Project of Guizhou Province (KY[2018]047), Guizhou University of Finance and Economics (2018XZD01) and Foundation of Science and Technology of Guizhou Province ([2019]1051).

Author information

Authors and Affiliations

  1. Guizhou Key Laboratory of Economics System Simulation, Guizhou University of Finance and Economics, Guiyang, 550004, PR China

    Changjin Xu

  2. College of Economics and Statistics, Guangzhou University, Guangzhou, 510006, PR China

    Wei Zhang

  3. School of Mathematics and Statistics, Guizhou University of Finance and Economics, Guiyang, 550004, PR China

    Zixin Liu

  4. School of Mathematics and Statistics, Henan University of Science and Technology, Luoyang, 471023, PR China

    Peiluan Li

  5. Library, Guizhou University of Finance and Economics, Guiyang, 550004, PR China

    Lingyun Yao

Authors
  1. Changjin Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wei Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zixin Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Peiluan Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Lingyun Yao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Wei Zhang.

Ethics declarations

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, C., Zhang, W., Liu, Z. et al. Bifurcation Study for Fractional-Order Three-Layer Neural Networks Involving Four Time Delays. Cogn Comput 14, 714–732 (2022). https://doi.org/10.1007/s12559-021-09939-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12559-021-09939-1

Keywords