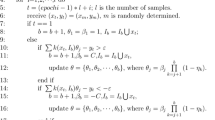Abstract
Bayesian inference is an important research area in cognitive computation due to its ability to reason under uncertainty in machine learning. As a representative algorithm, Stein variational gradient descent (SVGD) and its variants have shown promising successes in approximate inference for complex distributions. In practice, we notice that the kernel used in SVGD-based methods has a decisive effect on the empirical performance. Radial basis function (RBF) kernel with median heuristics is a common choice in previous approaches, but unfortunately, this has proven to be sub-optimal. Inspired by the paradigm of Multiple Kernel Learning (MKL), our solution to this flaw is using a combination of multiple kernels to approximate the optimal kernel, rather than a single one which may limit the performance and flexibility. Specifically, we first extend Kernelized Stein Discrepancy (KSD) to its multiple kernels view called Multiple Kernelized Stein Discrepancy (MKSD) and then leverage MKSD to construct a general algorithm Multiple Kernel SVGD (MK-SVGD). Further, MK-SVGD can automatically assign a weight to each kernel without any other parameters, which means that our method not only gets rid of optimal kernel dependence but also maintains computational efficiency. Experiments on various tasks and models demonstrate that our proposed method consistently matches or outperforms the competing methods.


Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data Availability
The datasets analyzed during the current study are available in the following repository, https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html for Covtype data and https://archive.ics.uci.edu/ml/datasets.php for all UCI datasets.
References
Faix M, Mazer E, Laurent R, Abdallah MO, LeHy R, Lobo J. Cognitive computation: a bayesian machine case study. In: 2015 IEEE 14th International Conference on Cognitive Informatics & Cognitive Computing (ICCI* CC). IEEE. 2015;67-75.
Chater N, Oaksford M, Hahn U, Heit E. Bayesian models of cognition. Wiley Interdisciplinary Reviews: Cognitive Science. 2010;1(6):811–23.
Knill DC, Richards W. Perception as Bayesian inference. Cambridge University Press. 1996.
Neal RM, et al. MCMC using Hamiltonian dynamics. Handbook of markov chain monte carlo. 2011;2(11):2.
Hoffman MD, Gelman A. The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J Mach Learn Res. 2014;15(1):1593–623.
Zhang R, Li C, Zhang J, Chen C, Wilson AG. Cyclical Stochastic Gradient MCMC for Bayesian Deep Learning. International Conference on Learning Representations. 2020.
Kingma DP, Welling M. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114. 2013.
Blei DM, Kucukelbir A, McAuliffe JD. Variational inference: A review for statisticians. J Am Stat Assoc. 2017;112(518):859–77.
Liu Q, Wang D. Stein variational gradient descent: A general purpose bayesian inference algorithm. In: Adv Neural Inf Process Syst. 2016;2378-86.
Chen C, Zhang R, Wang W, Li B, Chen L. A unified particle-optimization framework for scalable Bayesian sampling. arXiv preprint arXiv:1805.11659. 2018.
Liu C, Zhuo J, Cheng P, Zhang R, Zhu J, Carin L. Accelerated first-order methods on the Wasserstein space for Bayesian inference. stat. 2018;1050:4.
Zhang J, Zhang R, Carin L, Chen C. Stochastic particle-optimization sampling and the non-asymptotic convergence theory. In: International Conference on Artificial Intelligence and Statistics. PMLR. 2020;1877-87.
Zhang C, Li Z, Qian H, Du X. DPVI A Dynamic-Weight Particle-Based Variational Inference Framework. arXiv preprint arXiv:2112.00945. 2021.
Liu C, Zhuo J, Cheng P, Zhang R, Zhu J. Understanding and accelerating particle-based variational inference. In: International Conference on Machine Learning. 2019;4082-92.
Han J, Liu Q. Stein variational gradient descent without gradient. In: International Conference on Machine Learning. PMLR. 2018;1900-8.
Detommaso G, Cui T, Marzouk Y, Spantini A, Scheichl R. A Stein variational Newton method. In: Adv Neural Inf Process Syst. 2018;9169-79.
Wang D, Tang Z, Bajaj C, Liu Q. Stein variational gradient descent with matrix-valued kernels. In: Adv Neural Inf Process Syst. 2019;7836-46.
Gorham J, Mackey L. Measuring sample quality with kernels. In: International Conference on Machine Learning. PMLR. 2017;1292-301.
Hofmann T, Schölkopf B, Smola AJ. Kernel methods in machine learning. The annals of statistics. 2008;1171-220.
Han J, Ding F, Liu X, Torresani L, Peng J, Liu Q. Stein variational inference for discrete distributions. In: International Conference on Artificial Intelligence and Statistics. PMLR. 2020;4563-72.
Liu Q, Lee J, Jordan M. A kernelized Stein discrepancy for goodness-of-fit tests. In: International conference on machine learning. 2016;276-84.
Berlinet A, Thomas-Agnan C. Reproducing kernel Hilbert spaces in probability and statistics. Springer Science & Business Media. 2011.
Stein C. A bound for the error in the normal approximation to the distribution of a sum of dependent random variables. In: Proceedings of the sixth Berkeley symposium on mathematical statistics and probability, volume 2: Probability theory. vol.6. University of California Press. 1972;583-603.
Barbour AD, Chen LH. Steins (magic) method. arXiv preprint arXiv:1411.1179. 2014.
Gorham J. Measuring sample quality with Stein’s method. Stanford University. 2017.
Wilson AG, Hu Z, Salakhutdinov R, Xing EP. Deep kernel learning. In: Artificial intelligence and statistics. PMLR. 2016;370-8.
Kang Z, Lu X, Yi J, Xu Z. Self-weighted multiple kernel learning for graph-based clustering and semi-supervised classification. In: Proceedings of the 27th International Joint Conference on Artificial Intelligence. 2018;2312-8.
Xu Z, Jin R, King I, Lyu M. An extended level method for efficient multiple kernel learning. In: Adv Neural Inf Process Syst. 2009;1825-32.
Xu Z, Jin R, Yang H, King I, Lyu MR. Simple and efficient multiple kernel learning by group lasso. In: Proceedings of the 27th international conference on machine learning (ICML-10). Citeseer. 2010;1175-82.
Gönen M, Alpaydın E. Multiple kernel learning algorithms. J Mach Learn Res. 2011;12:2211–68.
Huang S, Kang Z, Tsang IW, Xu Z. Auto-weighted multi-view clustering via kernelized graph learning. Pattern Recognit. 2019;88:174–84.
Zhang Q, Kang Z, Xu Z, Huang S. Fu H. Spaks: Self-paced multiple kernel subspace clustering with feature smoothing regularization. Knowl Based Syst. 2022;109500.
Pan Z, Zhang H, Liang C, Li G, Xiao Q, Ding P, et al. Self-Weighted Multi-Kernel Multi-Label Learning for Potential miRNA-Disease Association Prediction. Molecular Therapy-Nucleic Acids. 2019;17:414–23.
Feng Y, Wang D, Liu Q. Learning to draw samples with amortized stein variational gradient descent. arXiv preprint arXiv:1707.06626. 2017.
Pu Y, Gan Z, Henao R, Li C, Han S, Carin L. Vae learning via stein variational gradient descent. In: Adv Neural Inf Process Syst. 2017;4236-45.
Li Y, Turner RE. Gradient estimators for implicit models. arXiv preprint http://arxiv.org/abs/1705.07107.
Korba A, Salim A, Arbel M, Luise G, Gretton A. A non-asymptotic analysis for Stein variational gradient descent. Adv Neural Inf Process Syst. 2020;33:4672–82.
Liu X, Tong X, Liu Q. Profiling pareto front with multi-objective stein variational gradient descent. Adv Neural Inf Process Syst. 2021;34.
Chen P, Ghattas O. Projected Stein variational gradient descent. Adv Neural Inf Process Syst. 2020;33:1947–58.
Jaini P, Holdijk L, Welling M. Learning Equivariant Energy Based Models with Equivariant Stein Variational Gradient Descent. Adv Neural Inf Process Syst. 2021;34.
Ba J, Erdogdu MA, Ghassemi M, Sun S, Suzuki T, Wu D, etal. Understanding the Variance Collapse of SVGD in High Dimensions. In: International Conference on Learning Representations. 2021.
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. J Mach Learn Res. 2011;12(7).
Hernández-Lobato JM, Adams R. Probabilistic backpropagation for scalable learning of bayesian neural networks. In: International Conference On Machine Learning. PMLR. 2015; 1861-9.
Funding
This paper was funded by the National Key Research and Development Program of China (No. 2018AAA0100204), and a key program of fundamental research from Shenzhen Science and Technology Innovation Commission (No. JCYJ20200109113403826). This work was also partially supported by Guangdong Provincial Key Laboratory of Novel Security Intelligence Technologies (No. 2022B1212010005).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethical Approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed Consent
Informed consent was not required as no humans or animals were involved.
Conflict of Interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Definitions
Definition 2
(Strictly Positive Kernel) For any function f that satisfies \(0 \le \Vert f\Vert _2^2 \le \infty\), a kernel \(k(x,x')\) is said to be integrally strictly positive definition if
Definition 3
(Stein Class) For a smooth function \(f: \mathcal {X} \rightarrow \mathbb {R}\), then, we can say that f is in the Stein class of q if satisfies
Definition 4
(Kernel in Stein Class) If kernel \(k\left( x, x^{\prime }\right)\) has continuous second-order partial derivatives, and for any fixed x, both \(k(x, \cdot )\) and \(k(\cdot , x)\) are in the Stein class of p, then the kernel \(k\left( x, x^{\prime }\right)\) said to be in the Stein class of p.
Appendix B. Proof
Proof of Proposition 1
Proof
For the kernel \(k_{\textbf {w}}(x,x')=\sum _{i=1}^m w_i k_i(x,x')\), where \(\textbf {w} \in \mathbb {R}_{+}^m, ||\textbf {w}||_{2}=1\), and \(k_i(x,x')\) is in the Stein class. According to Definition 4, we know that \(k_i(x,x')\) has continuous second-order partial derivatives. Setting \(g_i\) be the continuous second-order partial, we know that the continuous second-order partial g of multiple kernel \(k_{\textbf {w}}\) is
So, the kernel \(k_{\textbf {w}}(x,x')=\sum _{i=1}^m w_i k_i(x,x')\), where \(\textbf {w} \in \mathbb {R}_{+}^m, ||\textbf {w}||_{2}=1\), is in the Stein class.
Proof of Proposition 2
Proof
We know \(\mathbb {S}_{k_i}(q\Vert p) \ge 0\) and \(\mathbb {S}_{k_i}(q\Vert p) = 0\) if and only if \(q=p\) a.e. This means \(\mathbb {S}_{k_{\textbf {w}}} \ge 0\) and \(\mathbb {S}_{k_{\textbf {w}}}(q,p) = 0\) when \(q = p\) a.e. for any \(\textbf {w} \in \mathbb {R}_{+}^{m}\). Then, we know \(\mathbb {S}_{k_{\textbf {w}}}(q,p) = 0\) if and only if \(\mathbb {S}_{k_i}(q,p) = 0\). Thus \(q = p\) a.e.
Appendix C. Comparison to Matrix-SVGD (average)
Although using a similar “mixture” form, our approach is intrinsically different from Matrix-SVGD (average). Next, we will detailedly compare the two methods from theoretical aspect.
To elaborate more clearly, we briefly review the “mixture preconditioning kernel” in the Matrix-SVGD, which has the form of:
where \(\varvec{K}_{\varvec{Q}_{\ell }}\left( \varvec{x}, \varvec{x}^{\prime }\right)\) is defined as
and \(w_{\ell }(\varvec{x})\) is defined as
\(\varvec{K}_{0}\) can be chosen to be the standard RBF kernel and \(\mathcal {N}\) is Gaussian distribution.
The kernel used in our method is defined as
as shown in Eq. (13) in “ Multiple Kernelized Stein Discrepancy’’. Therefore, we can summarize the difference between the two as follows.
-
Different RKHS. The Matrix-SVGD introduces the optimization problem to vector-valued RKHS with matrix-valued kernels, while our method focuses on leveraging the effectiveness of Multiple Kernel Learning, which optimizes the objective in scalar-valued RKHS. So, the value of kernel \(\varvec{K}_{\varvec{Q}_{\ell }}\left( \varvec{x}, \varvec{x}^{\prime }\right)\) in Eq. (25) is a matrix while our kernel is still a scalar. The resultant value of the mixture kernel is also different: vector-value for Matrix-SVGD and scalar-value for ours.
-
Different roles. In Matrix-SVGD(average), the “mixture” form was introduced to address the intractability of the “Point-wise Preconditioning” matrix, which is done by using a weighted combination of several constant preconditioning matrices associated with a set of anchor points. In contrast, taking inspiration from the paradigm of multiple kernel learning, we utilize a more powerful “mixture” kernel instead of a single one to approximate the optimal kernel.
-
Different weight’s updating way. According to Eq. (27), we know that the kernel’s weight is the product of two Gaussian mixture probability from the anchor points, in which the weight’s distribution is pre-defined. While in our method, the optimal weight of each kernel is learned automatically, as shown in Eq. (21) in “SVGD with Multiple Kernels’’.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ai, Q., Liu, S., He, L. et al. Stein Variational Gradient Descent with Multiple Kernels. Cogn Comput 15, 672–682 (2023). https://doi.org/10.1007/s12559-022-10069-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12559-022-10069-5