Skip to main content

Advertisement

Springer Nature Link
Log in

Interval fuzzy number-based approach for modeling an uncertain fuzzy yield learning process

  • Original Research
  • Published:
Journal of Ambient Intelligence and Humanized Computing Aims and scope Submit manuscript

Abstract

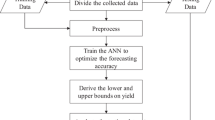
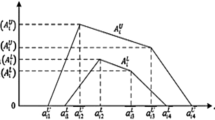
An interval fuzzy number-based approach was proposed in this study to model an uncertain yield learning process. The study aimed to overcome the limitations of present methods, wherein the lower and upper bounds of the yield are generally determined by few extreme cases, thus resulting in an unacceptable widening of the yield range. In the proposed interval fuzzy number-based approach, the range of yield was divided into two sections, namely inner and outer sections, which corresponded with the lower and upper membership functions of a fuzzy yield forecast based on interval fuzzy numbers, respectively. To fulfill different managerial objectives, in this approach, all actual values are included in the outer section, whereas most of these values fall within the inner section. To derive the values of parameters in a fuzzy yield learning model based on interval fuzzy numbers, a mixed binary nonlinear programming model was proposed and optimized. The interval fuzzy number-based approach was applied to two real-time cases for evaluating its effectiveness. According to experimental results, the performance of the proposed method was superior to that of several existing methods, particularly in terms of forecasting precision for the average range. Forecasting accuracy obtained using the interval fuzzy number-based approach was satisfactory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  • Ashtiani B, Haghighirad F, Makui A, ali Montazer G (2009) Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets. Appl Soft Comput 9(2):457–461

    Article  Google Scholar 

  • Atanassov K, Gargov G (1989) Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31(3):343–349

    Article  MathSciNet  Google Scholar 

  • Baležentis T, Zeng S (2013) Group multi-criteria decision making based upon interval-valued fuzzy numbers: an extension of the MULTIMOORA method. Expert Syst Appl 40(2):543–550

    Article  Google Scholar 

  • Baron M, Takken A, Yashchin E, Lanzerotti M (2008) Modeling and forecasting of defect-limited yield in semiconductor manufacturing. IEEE Trans Semicond Manuf 21(4):614–624

    Article  Google Scholar 

  • Blancett RS (2002) Learning from productivity learning curves. Res Technol Manag 45(3):54–58

    Article  Google Scholar 

  • Cabrerizo FJ, Pérez IJ, Herrera-Viedma E (2010) Managing the consensus in group decision making in an unbalanced fuzzy linguistic context with incomplete information. Knowl Based Syst 23(2):169–181

    Article  Google Scholar 

  • Chen T (2012) Ahybrid fuzzy and neural approach with virtual experts and partial consensus for DRAM price forecasting. Int J Innov Comput Inf Control 8(1B):583–598

    Google Scholar 

  • Chen T (2017) A heterogeneous fuzzy collaborative intelligence approach for forecasting the product yield. Appl Soft Comput 57:210–224

    Article  Google Scholar 

  • Chen T (2018) An innovative fuzzy and artificial neural network approach for forecasting yield under an uncertain learning environment. J Ambient Intell Humaniz Comput 9:1013–1025

    Article  Google Scholar 

  • Chen T, Lin YC (2008) A fuzzy-neural system incorporating unequally important expert opinions for semiconductor yield forecasting. Int J Uncertain Fuzziness Knowl Based Syst 16(1):35–58

    Article  Google Scholar 

  • Chen TCT, Lin CW (2018) An innovative yield learning model considering multiple learning sources and learning source interactions. Comput Ind Eng (in press)

  • Chen T, Wang MJ (1999) A fuzzy set approach for yield learning modeling in wafer manufacturing. IEEE Trans Semicond Manuf 12(2):252–258

    Article  Google Scholar 

  • Chen T, Wang YC (2014) An agent-based fuzzy collaborative intelligence approach for precise and accurate semiconductor yield forecasting. IEEE Trans Fuzzy Syst 22(1):201–211

    Article  Google Scholar 

  • Dahooie JH, Zavadskas EK, Abolhasani M, Vanaki A, Turskis Z (2018) A novel approach for evaluation of projects using an interval-valued fuzzy additive ratio assessment (ARAS) method: a case study of oil and gas well drilling projects. Symmetry 10(2):45

    Article  Google Scholar 

  • Dimuro GP (2011) On interval fuzzy numbers. In: IEEE workshop-school on theoretical computer science, pp 3–8

  • Dong Y, Zhang H, Herrera-Viedma E (2016) Integrating experts’ weights generated dynamically into the consensus reaching process and its applications in managing non-cooperative behaviors. Decis Support Syst 84:1–15

    Article  Google Scholar 

  • Donoso S, Marin N, Vila MA (2006) Quadratic programming models for fuzzy regression. In: Proceedings of international conference on mathematical and statistical modeling in honor of Enrique Castillo

  • Dunham W (1990) Journey through genius: the great theorems of mathematics. Wiley, New York

    MATH  Google Scholar 

  • Gruber H (1994) Learning and strategic product innovation: theory and evidence for the semiconductor industry. Elsevier Science B. V, The Netherlands

    Google Scholar 

  • Guijun W, Xiaoping L (1998) The applications of interval-valued fuzzy numbers and interval-distribution numbers. Fuzzy Sets Syst 98(3):331–335

    Article  MathSciNet  Google Scholar 

  • Herrera-Viedma E, Cabrerizo FJ, Kacprzyk J, Pedrycz W (2014) A review of soft consensus models in a fuzzy environment. Inf Fusion 17:4–13

    Article  Google Scholar 

  • Huang D, Chen T, Wang MJJ (2001) A fuzzy set approach for event tree analysis. Fuzzy Sets Syst 118(1):153–165

    Article  MathSciNet  Google Scholar 

  • Jaeger H, Haas H (2004) Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304(5667):78–80

    Article  Google Scholar 

  • Keršuliene V, Zavadskas EK, Turskis Z (2010) Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J Bus Econ Manag 11(2):243–258

    Article  Google Scholar 

  • Krueger DC, Montgomery DC, Mastrangelo CM (2011) Application of generalized linear models to predict semiconductor yield using defect metrology data. IEEE Trans Semicond Manuf 24(1):44–58

    Article  Google Scholar 

  • Kulkarni SS (2006) The impact of uncertain yield on capacity acquisition in process plant networks. Math Comput Model 43(7–8):704–717

    Article  Google Scholar 

  • Lee CS, Chung CC, Lee HS, Gan GY, Chou MT (2016) An interval-valued fuzzy number approach for supplier selection. J Mar Sci Technol 24(3):384–389

    Google Scholar 

  • Liu P, Jin F (2012) A multi-attribute group decision-making method based on weighted geometric aggregation operators of interval-valued trapezoidal fuzzy numbers. Appl Math Model 36(6):2498–2509

    Article  MathSciNet  Google Scholar 

  • Moore RE (1979) Methods and applications of interval analysis. SIAM, Philadelphia

    Book  Google Scholar 

  • Peters G (1994) Fuzzy linear regression with fuzzy intervals. Fuzzy Sets Syst 63:45–55

    Article  MathSciNet  Google Scholar 

  • Rashid T, Beg I, Husnine SM (2014) Robot selection by using generalized interval-valued fuzzy numbers with TOPSIS. Appl Soft Comput 21:462–468

    Article  Google Scholar 

  • Shu MH, Wu HC (2010) Measuring the manufacturing process yield based on fuzzy data. Int J Prod Res 48(6):1627–1638

    Article  Google Scholar 

  • Tanaka H, Watada J (1988) Possibilistic linear systems and their application to the linear regression model. Fuzzy Sets Syst 272:275–289

    Article  MathSciNet  Google Scholar 

  • Tirkel I (2013) Yield learning curve models in semiconductor manufacturing. IEEE Trans Semicond Manuf 26(4):564–571

    Article  Google Scholar 

  • Tirkel I, Rabinowitz G, Price D, Sutherland D (2016) Wafer fabrication yield learning and cost analysis based on in-line inspection. Int J Prod Res 54(12):3578–3590

    Article  Google Scholar 

  • Wang CX (2009) Random yield and uncertain demand in decentralised supply chains under the traditional and VMI arrangements. Int J Prod Res 47(7):1955–1968

    Article  Google Scholar 

  • Wei SH, Chen SM (2009) Fuzzy risk analysis based on interval-valued fuzzy numbers. Expert Syst Appl 36(2):2285–2299

    Article  Google Scholar 

  • Wei G, Zhao X, Lin R (2013) Some hesitant interval-valued fuzzy aggregation operators and their applications to multiple attribute decision making. Knowl Based Syst 46:43–53

    Article  Google Scholar 

  • Wu HC, Chen T (2015) CART–BPN approach for estimating cycle time in wafer fabrication. J Ambient Intell Humaniz Comput 6(1):57–67

    Article  Google Scholar 

  • Zhang C, Wang C, Zhang Z, Tian D (2018) A novel technique for multiple attribute group decision making in interval-valued hesitant fuzzy environments with incomplete weight information. J Ambient Intell Humaniz Comput. https://doi.org/10.1007/s12652-018-0912-2

    Article  Google Scholar 

Download references

Acknowledgements

This study was sponsored by the Ministry of Science and Technology, Taiwan.

Author information

Authors and Affiliations

  1. Department of Industrial Engineering and Management, National Chiao Tung University, 1001, University Road, Hsinchu, 300, Taiwan

    Toly Chen

  2. Department of Industrial Engineering and Management, Chaoyang University of Technology, 168, Jifeng E. Rd., Wufeng District, Taichung City, 41349, Taiwan, ROC

    Yu-Cheng Wang

Authors
  1. Toly Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yu-Cheng Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yu-Cheng Wang.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, T., Wang, YC. Interval fuzzy number-based approach for modeling an uncertain fuzzy yield learning process. J Ambient Intell Human Comput 11, 1213–1223 (2020). https://doi.org/10.1007/s12652-019-01302-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12652-019-01302-5

Keywords