Skip to main content

Advertisement

Springer Nature Link
Log in

Monarch butterfly optimized control with robustness analysis for grid tied centralized and distributed power generations

  • Original Research
  • Published:
Journal of Ambient Intelligence and Humanized Computing Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

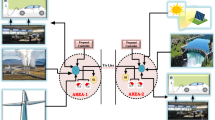
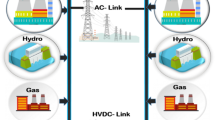
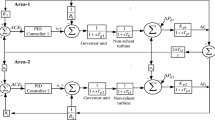
Modern power systems have emerged as a distributed complex interconnection of conventional as well as renewable energy resources and varied loads. Intermittent and varied nature of wind power has further posed major challenges towards control of voltage profile variations and frequency deviations in such integrated distributed power systems. This is because, such integrated renewable energy resources result in overall reduced system inertia that introduces complexity to load frequency control problem. In this paper, recently proposed heuristic algorithm known as Monarch Butterfly based Optimization has been extended to address frequency control problem arising due to sudden source and load fluctuation in a three-area test power system. The considered test system consists of both distributed and centralized power generations using Wind, Hydro, Gas and Steam. The controllers optimized using the proposed approach were simulated on MATLAB® and Simulink® platform. Simulation results validate effectiveness of proposed strategy vis-a-vis other existing techniques using Moth Search Algorithm, Elephant Herding Optimization.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Abbreviations

Δ\(AFCEi\) :

Area frequency control error

\(i\) :

Area number

R\(i\) :

Droop characteristic

\(D_{i}\) :

Area load frequency characteristic

\(B_{i}\) :

Frequency bias

\(Tij\) :

Synchronizing coefficient between area i and j

\(Tgi\) :

Governor time constant

\(Tti\) :

Turbine time constant (thermal unit)

\(Th1i\) :

Turbine time constant (hydro unit)

\(Th2i\) :

Turbine time constant (hydro unit)

\(Tw\) :

Turbine time constant (hydro unit)

\(w1\) :

Lead compensator parameter

\(w2\) :

Lead compensator parameter

\(Mi\left( {2Hi} \right)\) :

Area equivalent inertia

\(Th1i\) :

Turbine time constant (hydro unit)

\({\text{X}}_{c}\) :

Lead time constant of gas turbine speed governor, s

\(c_{g}\) :

Gas turbine valve positioned

\({\text{T}}_{fc}\) :

Gas turbine fuel time constant, s

\({\text{T}}_{cd}\) :

Gas turbine compressor discharge volume-time constant, s

Δ\(fi\) :

Change in area frequency (pu Hz)

Δ\(Pgi,j\) :

Change in governor valve position (pu)

Δ\(Ptiei,j\) :

Tie-line power deviation (pu)

\({\text{Y}}_{c}\) :

Lag time constant of gas turbine speed governor, s

\(b_{gt}\) :

Gas turbine constant of valve positioner, s

\({\text{T}}_{cr}\) :

Gas turbine combustion reaction time delay, s

\({\text{K}}_{g}\) :

Participation factors of thermal, hydro and gas generating units, respectively

Δ\(Pci\) :

Change in governor load set point (pu)

Δ\(Ptubi\) :

Change in turbine power (pu)

Δ\(PLi\) :

Power demand deviation (pu)

\(H_{e}\) :

Wind turbine rotor inertia constant

\(Ta\) :

Time constant of electrical power converter

\(Kwp\) :

Proportional gain of speed controller

\(Tr\) :

Transducer time constant, s

\(Tp\) :

Time constant of pitch controller,s

\(Kwi\) :

Integral gain of speed controller

\(Tw\) :

Washout filter time constant

References

  • Abdelmoume`ne D, Salem A, Lakhdar M (2018) Load frequency control problem in interconnected power systems using robust fractional PIkD controller. Ain Shams Eng J 9:77–88

    Article  Google Scholar 

  • Ali ES, Abd-Elazim SM (2013) BFOA based design of PID controller for two area Load Frequency Control with nonlinearities. Int J Electr Power Energy Syst 51:224–231

    Article  Google Scholar 

  • Bevrani H (2014) Robust power system frequency control, 2nd edn. Springer, New York

    MATH  Google Scholar 

  • Bhatt P, Roy R, Ghoshal SP (2011) Dynamic participation of doubly fed induction generator in automatic generation control. Renewable Energy 36:1203–1213

    Article  Google Scholar 

  • Daneshfar F, Bevrani H (2012) Multiobjective design of load frequency control using genetic algorithms. Int J Electr Power Energy Syst 42:257–263

    Article  Google Scholar 

  • Dey R, Ghosh S, Ray G, Rakshit A (2012) H-infinity load frequency control of interconnected power systems with communication delays. Int J Electr Power Energy Syst 42:672–684

    Article  Google Scholar 

  • Dhillon SS, Lather JS, Marwaha S (2016) Multi objective load frequency control using hybrid bacterial foraging and particle swarm optimized PI controller. Int J Electr Power Energy Syst 79:196–209

    Article  Google Scholar 

  • Dhillon SS, Agarwal S, Wang GG, Lather JS (2020) Automatic generation control of interconnected power systems using elephant herding optimization. Intell Comput Tech Smart Energy Syst Lect Notes Electr Eng 607:9–18

    Google Scholar 

  • Diambomba HT, Yanxia S (2019) Load frequency controllers considering renewable energy integration in power system. Energy Rep 5:436–453

    Article  Google Scholar 

  • Ersdal MA, Imsland L, Uhlen K (2016) Model predictive load-frequency control. IEEE Trans Power Syst 31:777–785

    Article  Google Scholar 

  • Franz G, Tedesco F (2011) Constrained load/frequency control problems in networked multi-area power systems. J Franklin Inst 348:832–852

    Article  Google Scholar 

  • Golshannavaz S, Khezri R, Esmaeeli M, Siano P (2018) A two-stage robust-intelligent controller design for efficient LFC based on Kharitonov theorem and fuzzy logic. J Ambient Intell Hum Comput 9(5):1445–1454

    Article  Google Scholar 

  • Hassan Y (2015) Adaptive fuzzy logic load frequency control of multi-area power system. Int J Electr Power Energy Syst 68:384–395

    Article  Google Scholar 

  • Jizhen L, Qi Y, Yang H (2019) Model predictive control for load frequency of hybrid power system with wind power and thermal power. Energy 172:555–565

    Article  Google Scholar 

  • Khan ZA, Zafar A, Javaid S, Aslam S, Rahim MH, Javaid N (2019) Hybrid meta-heuristic optimisation based home energy management system in smart grid. J Ambient Intell Hum Comput. https://doi.org/10.1007/s12652-018-01169-y

    Article  Google Scholar 

  • Mansour J (2011) DFIG based wind turbine contribution to system frequency control. Master thesis, the University of Waterloo, Canada

  • Marwaha S, Lather JS, Dhillon SS (2015) Multi area load frequency control using model predictive controller. In: Proceedings of international conference on electrical and electronics engineering. Thailand, pp 317–323

  • Mohanty B (2020) Hybrid flower pollination and pattern search algorithm optimized sliding mode controller for deregulated AGC system. J Ambient Intell Hum Comput 11:763–776

    Article  Google Scholar 

  • Naidu K, Mokhlis H, Bakar AHA (2014) Multi objective optimization using weighted sum Artificial Bee Colony algorithm for Load Frequency Control. Int J Electr Power Energy Syst 55:657–667

    Article  Google Scholar 

  • Nattapol S, Issarachai N (2015) Intelligent photovoltaic farms for robust frequency stabilization in multi-area interconnected power system based on PSO-based optimal Sugeno fuzzy logic control. Renew Energy 74:555–567

    Article  Google Scholar 

  • Parmar KP, Majhi S, Kothari DP (2012) Load frequency control of a realistic power system with multi-source power generation. Int J Electr Power Energy Syst 42:426–433

    Article  Google Scholar 

  • Prakasha S, Sinhab SK (2014) Simulation based neuro-fuzzy hybrid intelligent PI control approach in four-area load frequency control of interconnected power system. Appl Soft Comput 23:152–164

    Article  Google Scholar 

  • Rajesh KS, Dash SS (2019) Load frequency control of autonomous power system using adaptive fuzzy based PID controller optimized on improved sine cosine algorithm. J Ambient Intell Hum Comput 10(6):2361–2373

    Article  Google Scholar 

  • Saikia LC, Nanda J, Mishra S (2011) Performance comparison of several classical controllers in AGC for multi-area interconnected thermal system. Int J Electr Power Energy Syst 33:394–401

    Article  Google Scholar 

  • Shyree SB, Kamaraj N (2016) Hybrid Neuro Fuzzy approach for automatic generation control in restructured power system. Int J Electr Power Energy Syst 74:274–285

    Article  Google Scholar 

  • Tan W, Zhou H (2012) Robust analysis of decentralized load frequency control for multi-area power systems. Int J Electr Power Energy Syst 43:996–1005

    Article  Google Scholar 

  • Wang GG (2016) Moth search algorithm: a bio-inspired metaheuristic algorithm for global optimization problems. Memet Comput 10:151–164

    Article  Google Scholar 

  • Wang GG, Deb S, Leandro dos Santos Coelho (2015) Elephant Herding Optimization. In: Proceedings of IEEE 3rd international symposium on computational and business intelligence (ISCBI 2015),Bali, Indonesia

  • Yang TC, Ding ZT, Yu H (2002) Decentralised power system Load Frequency control beyond the limit of diagonal domianance. Electr Power Energy Syst 24:173–184

    Article  Google Scholar 

  • Zamani AA, Bijami E, Sheikholeslam F, Jafrasteh B (2014) Optimal fuzzy load frequency controller with simultaneous auto-tuned membership functions and fuzzy control rules. Turk J Electr Eng Comput Sci 22:66–86

    Article  Google Scholar 

  • Zhang X, Lu S, Liu S, Wang X (2016) A review on wide-area damping control to restrain inter-area low frequency oscillation for large-scale power systems with increasing renewable generation. Renew Sustain Energy Rev 57:45–58

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electrical and Electronics Engineering, Ajay Kumar Garg Engineering College, Ghaziabad, India

    Sukhwinder Singh Dhillon

  2. Department of Electrical Engineering, National Institute of Technology, Kurukshetra, India

    J. S. Lather

  3. Department of Computer Science and Technology, Ocean University of China, Qingdao, 266100, China

    Gai-Ge Wang

  4. Department of Information Technology, Ajay Kumar Garg Engineering College, Ghaziabad, India

    P. Kaur

  5. State Key Laboratory of Industrial Control Technology, College of Control Science and Engineering, Zhejiang University, Hangzhou, China

    Lalitesh Kumar

Authors
  1. Sukhwinder Singh Dhillon
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. J. S. Lather
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Gai-Ge Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. P. Kaur
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Lalitesh Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Sukhwinder Singh Dhillon.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

(i) Parameters for Hydro power unit (Ali and Abd-Elazim 2013; Naidu et al. 2014; Dhillon et al. 2016)

Parameter

Value

Parameter

Value

\(K_{H}\)

0.3261

\(T_{w}\)

1 s

\(T_{rs}\)

5 s

\(T_{rh}\)

28.75 s

\(T_{gh}\)

0.2 s

\(R_{h}\)

2.4 Hz/pu MW

\(B_{h}\)

0.4312 pu MW/Hz

\(B_{g}\)

0.4312 puMW/Hz

(ii) Parameters for Gas power unit (Ali and Abd-Elazim 2013; Naidu et al. 2014; Dhillon et al. 2016)

Parameter

Value

Parameter

Value (s)

\(K_{g}\)

0.1304

\(b_{g}\)

0.5

\(C_{g}\)

1 s

\(X_{c}\)

0.6

\(Y_{c}\)

1 s

\(T_{cr}\)

0.01

\(T_{fc}\)

0.23 s

\(T_{cd}\)

0.2

\(R_{g}\)

2.4 Hz/pu MW

  

(iii) Parameters for Steam power unit (Bevrani 2014)

Parameter

Value

Parameter

Value

Parameter

Value

\(T_{t1}\)

0.44

\(T_{t2}\)

0.44

\(T_{t3}\)

0.3

\(H_{1}\)

0.1667

\(H_{2}\)

0.2

\(H_{3}\)

0.1247

\(D_{1}\)

0.015

\(D_{2}\)

0.2017

\(D_{3}\)

0.015

\(R_{1}\)

3

\(R_{2}\)

2.73

\(R_{3}\)

2.73

\(B_{1}\)

0.3483

\(B_{2}\)

0.3827

\(B_{3}\)

0.3827

\(T_{g1}\)

0.08

\(T_{g2}\)

0.06

\(T_{g3}\)

0.07

(iv) Parameters for DFIG-wind turbine unit (Mansour 2011)

Parameter

Value

Parameter

Value

Parameter

Value

\(T_{p}\)

1.0

\(T_{a}\)

0.2

\(T_{w}\)

6

\(T_{t}\)

0.1

\(K_{wi}\)

0.1

\(K_{wp}\)

1.61

\(R\)

3

\(H_{e}\)

3.5

\(T_{0}\)

0.07

\(K_{p1}\)

62

    

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dhillon, S., Lather, J.S., Wang, GG. et al. Monarch butterfly optimized control with robustness analysis for grid tied centralized and distributed power generations. J Ambient Intell Human Comput 13, 3595–3608 (2022). https://doi.org/10.1007/s12652-020-01992-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12652-020-01992-2

Keywords