Skip to main content

Advertisement

SpringerLink
Log in

Multi-period mean-semi-entropy portfolio management with transaction costs and bankruptcy control

  • Original Research
  • Published:
Journal of Ambient Intelligence and Humanized Computing Aims and scope Submit manuscript

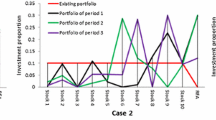
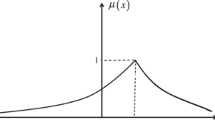
Abstract

This study investigates a multi-period portfolio management problem under fuzzy settings. For the first time, the newly proposed semi-entropy in the literature is employed as an efficient downside risk measure for risk control in multi-period portfolio optimization. Fuzzy techniques for financial modeling show advantageous performance when future financial market conditions cannot be effectively detected with only historical data. We describe the assert returns by fuzzy variables. Two realistic constraints of transaction costs and bankruptcy events are taken into consideration in our model formulation of a multi-period mean-semi-entropy optimization program. The formulated program is rewritten as a crisp single-objective nonlinear programming by introducing a risk-aversion factor, and final solution to the program is obtained by using genetic algorithm. For the demonstration of computational results, we provide a numerical example with real-life stock data, which illustrates the main modelling concept and the efficiency of genetic algorithm solving method. Comparative analyses over several baseline models show the advantages of adopting fuzzy semi-entropy as an efficient downside risk measure for multi-period portfolio investment optimization.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Bajeux-Besnainou I, Portait R (1998) Dynamic asset allocation in a mean-variance framework. Manag Sci 44(11):S79–S95

    MATH  Google Scholar 

  • Bertsimas D, Pachamanova D (2008) Robust multiperiod portfolio management in the presence of transaction costs. Comp Oper Res 35(1):3–17

    MathSciNet  MATH  Google Scholar 

  • Buckley JJ, Hayashi Y (1994) Fuzzy genetic algorithm and applications. Fuzzy Set Syst 61(2):129–136

    MathSciNet  Google Scholar 

  • Cai X, Teo KL, Yang X, Zhou XY (2000) Portfolio optimization under a minimax rule. Manag Sci 46(7):957–972

    MATH  Google Scholar 

  • Calafiore GC (2008) Multi-period portfolio optimization with linear control policies. Automatica 44(10):2463–2473

    MathSciNet  MATH  Google Scholar 

  • Chen ZP (2005) Multiperiod consumption and portfolio decisions under the multivariate GARCH model with transaction costs and CVaR-based risk control. OR Spectr 27(4):603–632

    MATH  Google Scholar 

  • Costa OLV, Araujo MV (2008) A generalized multi-period mean-variance portfolio optimization with Markov switching parameters. Automatica 44(10):2487–2497

    MathSciNet  MATH  Google Scholar 

  • D’Aniello G, Gaeta M, Tomasiello S, Raritá L (2016) A fuzzy consensus approach for group decision making with variable importance of experts. In: 2016 FUZZ-IEEE, pp 1693–1700

  • Dantzig GB, Infanger G (1993) Multi-stage stochastic linear programs for portfolio optimization. Ann Oper Res 45:59–76

    MathSciNet  MATH  Google Scholar 

  • Deng XT, Li ZF, Wang SY (2005) A minimax portfolio selection strategy with equilibrium. Eur J Oper Res 166(1):278–292

    MathSciNet  MATH  Google Scholar 

  • Elton EJ, Gruber MJ (1974) The multi-period consumption investment problem and single period analysis. Oxf Econ Papers 2:289–301

    Google Scholar 

  • Fang SC, Rajasekera JR, Tsao HSJ (1997) Entropy optimization and mathematical programming. Kluwer Academic Publisheres, Dordrecht

    MATH  Google Scholar 

  • Fang Y, Lai KK, Wang SY (2006) Portfolio rebalancing model with transaction costs based on fuzzy decision theory. Eur J Oper Res 175(2):879–893

    MATH  Google Scholar 

  • Fu C, Lari-Lavassani A, Li X (2010) Dynamic mean-variance portfolio selection with borrowing constraint. Eur J Oper Res 200(1):312–319

    MathSciNet  MATH  Google Scholar 

  • Gülpınar N, Rustem B (2007) Worst-case robust decisions for multi-period mean-variance portfolio optimization. Eur J Oper Res 183(3):981–1000

    MathSciNet  MATH  Google Scholar 

  • Hakansson NH (1971) Multi-period mean-variance analysis: toward a general theory of portfolio choice. J Finance 26:857–884

    Google Scholar 

  • Huang XX, Ying H (2013) Risk index based models for portfolio adjusting problem with returns subject to experts’ evaluations. Econ Model 30:61–66

    Google Scholar 

  • Hibiki N (2006) Multi-period stochastic optimization models for dynamic asset allocation. J Bank Finance 30(2):365–390

    Google Scholar 

  • Holland JH (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor

    Google Scholar 

  • Inuiguchi M, Ramik J (2000) Possibilistic linear programming: A brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Set Syst 111(1):3–28

    MathSciNet  MATH  Google Scholar 

  • Inuiguchi M, Tanino T (2000) Portfolio selection under independent possibilistic information. Fuzzy Set Syst 115(1):83–92

    MathSciNet  MATH  Google Scholar 

  • Jana P, Roy TK, Mazumder SK (2009) Multi-objective possibilistic model for portfolio selection with transaction cost. J Comput Appl Math 228(1):188–196

    MathSciNet  MATH  Google Scholar 

  • Kapur JN (1990) Maximum entropy models in science and engineering. Wiley Eastern Limited, New Delhi

    MATH  Google Scholar 

  • Li D, Ng WL (2000) Optimal dynamic portfolio selection: multiperiod mean-variance formulation. Math Finance 10(3):387–406

    MathSciNet  MATH  Google Scholar 

  • Li X, Liu B (2006) A sufficient and necessary condition for credibility measures. Int J Uncertain Fuzz 14(05):527–535

    MathSciNet  MATH  Google Scholar 

  • Li X, Qin ZF, Kar S (2010) Mean-variance-skewness model for portfolio selection with fuzzy returns. Eur J Oper Res 202(1):239–247

    MATH  Google Scholar 

  • Li X (2013) Credibilistic programming. Springer, New York

    MATH  Google Scholar 

  • Li ZM, Zhang Q, Du XY, Qian XY, Lev B (2019) A hesitant fuzzy multi-criteria group decision making method for college applicants’ learning potential evaluation. J Data Inform Manag 1(1–2):65–75

    Google Scholar 

  • Ling A, Sun J, Wang M (2019) Robust multi-period portfolio selection based on downside risk with asymmetrically distributed uncertainty set. Eur J Oper Res. https://doi.org/10.1016/j.ejor.2019.01.012

    Article  MATH  Google Scholar 

  • Liu BD, Iwamura K (1998) Chance constrained programming with fuzzy parameters. Fuzzy Set Syst 94(2):227–237

    MathSciNet  MATH  Google Scholar 

  • Liu BD (2000) Dependent-chance programming in fuzzy environments. Fuzzy Set Syst 109(1):97–106

    MathSciNet  MATH  Google Scholar 

  • Liu BD, Liu Y-K (2002) Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans Fuzzy Syst 10(4):445–450

    Google Scholar 

  • Liu Y-K, Liu B (2003) Expected value operator of random fuzzy variable and random fuzzy expected value models. Int J Uncertain Fuzz 11(2):195–215

    MathSciNet  MATH  Google Scholar 

  • Liu BD (2003) Inequalities and convergence concepts of fuzzy and rough variables. Fuzzy Optim Decis Making 2(2):87–100

    MathSciNet  MATH  Google Scholar 

  • Liu BD (2010) Uncertainty theory: a branch of mathematics for modeling human uncertainty, 3rd edn. Springer, Berlin

    Google Scholar 

  • Liu YJ, Zhang WG, Xu WJ (2012) Fuzzy multi-period portfolio selection optimization models using multiple criteria. Automatica 48(12):3042–3053

    MathSciNet  MATH  Google Scholar 

  • Liu F, Yu Q, Huang MJ, Ralescu DA (2020) An inconsistency index of interval additive reciprocal matrices with application to group decision making. J Data Inform Manag. https://doi.org/10.1007/s42488-019-00019-6

    Article  Google Scholar 

  • Markowitz H (1952) Portfolio selection. J Finance 7(1):77–91

    Google Scholar 

  • Markowitz H (1987) Mean-variance analysis in portfolio choice and capital markets. Blackwell, Oxford

    MATH  Google Scholar 

  • Markowitz H, Todd P, Xu G, Yamane Y (1993) Computation of mean-semivariance efficient sets by the critical line algorithm. Ann Oper Res 45(1):307–317

    MathSciNet  MATH  Google Scholar 

  • Mossin J (1968) Optimal multiperiod portfolio polices. J Bus 41:215–229

    Google Scholar 

  • Patel NR, Subrahmanyam MG (1982) A simple algorithm for optimal portfolio selection with fixed transaction costs. Manag Sci 28(3):303–314

    MathSciNet  MATH  Google Scholar 

  • Qin JD (2019) A survey of type-2 fuzzy aggregation and application for multiple criteria decision making. J Data Inform Manag 1(1–2):17–32

    Google Scholar 

  • Sadjadi SJ, Seyedhosseini SM, Hassanlou KH (2011) Fuzzy multiperiod portfolio selection with different rates for borrowing and lending. Appl Soft Comput 11(4):3821–3826

    Google Scholar 

  • Shen RJ, Zhang SZ (2008) Robust portfolio selection based on a multi-stage scenario tree. Eur J Oper Res 191(3):864–887

    MathSciNet  MATH  Google Scholar 

  • Takano Y, Gotoh JY (2014) Multi-period portfolio selection using kernel-based control policy with dimensionality reduction. Expert Syst Appl 41(8):3901–3914

    Google Scholar 

  • Vercher E, Bermúdez JD, Segura JV (2007) Fuzzy portfolio optimization under downside risk measures. Fuzzy Set Syst 158(7):769–782

    MathSciNet  MATH  Google Scholar 

  • Wang SY, Zhu SS (2002) On fuzzy portfolio selection problem. Fuzzy Opt Decis Making 1(4):361–377

    MathSciNet  MATH  Google Scholar 

  • Xia YS, Liu BD, Wang SY, Lai KK (2000) A model for portfolio selection with order of expected returns. Comput Oper Res 27(5):409–422

    MATH  Google Scholar 

  • Yan W, Miao R, Li SR (2007) Multi-period semi-variance portfolio selection: model and numerical solution. Appl Math Comput 194(1):128–134

    MathSciNet  MATH  Google Scholar 

  • Yan W, Li SR (2009) A class of multi-period semi-variance portfolio selection with a four-factor futures price model. J Appl Math Comput 29(1–2):19–34

    MathSciNet  MATH  Google Scholar 

  • Yin G, Zhou XY (2004) Markowitz’s mean-variance portfolio selection with regime witching: from discrete-time models to their continuous-time limits. IEEE Trans Autom Control 49(3):349–360

    MATH  Google Scholar 

  • Yu M, Takahashi S, Inoue H, Wang SY (2010) Dynamic portfolio optimization with risk control for absolute deviation model. Eur J Oper Res 201(2):349–364

    MathSciNet  MATH  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inform Control 8:338–353

    MATH  Google Scholar 

  • Zadeh LA (1978) Fuzzy sets as a basis for a theory of possibility. Fuzzy Set Syst 1:3–28

    MathSciNet  MATH  Google Scholar 

  • Zadeh LA (1979) A theory of approximate reasoning. In: Hayes et al (eds) Mathematical Frontiers of the Social and Policy Sciences. Westview Press, Boulder, pp 69–129

  • Zhang WG, Zhang XL, Chen YX (2011) Portfolio adjusting optimization with added assets and transaction costs based on credibility measures. Insur Math Econ 49:353–360

    MathSciNet  MATH  Google Scholar 

  • Zhang WG, Liu YJ, Xu WJ (2012) A possibilistic mean-semivariance-entropy model for multi-period portfolio selection with transaction costs. Eur J Oper Res 222:341–349

    MathSciNet  MATH  Google Scholar 

  • Zhang GQ, Zhang QQ (2019) Multiportfolio optimization with CVaR risk measure. J Data Inform Manag 1(3–4):91–106

    Google Scholar 

  • Zhou JD, Li X, Pedrycz W (2016) Mean-semi-entropy models of fuzzy portfolio selection. IEEE Trans Fuzzy Syst 24(6):1627–1636

    Google Scholar 

  • Zhou JD, Li X, Kar S, Zhang GQ, Yu HT (2017) Time consistent fuzzy multi-period rolling portfolio optimization with adaptive risk aversion factor. J Ambient Intell Human Comput 8(5):651–666

    Google Scholar 

  • Zhu SS, Li D, Wang SY (2004) Risk control over bankruptcy in dynamic portfolio selection: a generalized mean-variance. IEEE Trans Autom Control 49(3):447–457

    MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 71722007, 71931001), and the Funds for First-class Discipline Construction in China (No. XK1802-5).

Author information

Authors and Affiliations

  1. School of Data Science, City University of Hong Kong, Hong Kong, China

    Jiandong Zhou

  2. School of Economics and Management, Beijing University of Chemical Technology, Beijing, 100029, China

    Xiang Li

Authors
  1. Jiandong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiang Li.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants performed by any of the authors. This article does not contain any studies with animals performed by any of the authors. This article does not contain any studies with human participants or animals performed by any of the authors.

Informed consent

There is no individual participant included in the study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, J., Li, X. Multi-period mean-semi-entropy portfolio management with transaction costs and bankruptcy control. J Ambient Intell Human Comput 12, 705–715 (2021). https://doi.org/10.1007/s12652-020-02053-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12652-020-02053-4

Keywords

Search

Navigation