Sliding mode learning algorithm based adaptive neural observer strategy for fault estimation, detection and neural controller of an aircraft

Abstract

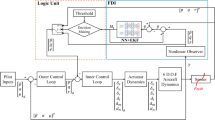
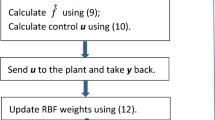
In this paper, two different adaptive strategies are presented for continuous time uncertain nonlinear systems with unknown disturbances and faults. In first strategy, a sliding mode control based adaptive neural observer approach is anticipated for estimation of unknown disturbances and faults by using the multi-layer perceptron, the weight parameters are updated by using the sliding mode online learning strategy. Conventionally, gradient descent back-propagation adaptation methods are used for neural networks training, within these adaptation methods a new theory of sliding mode control is added to conventional gradient descent back-propagation procedure. In this nonlinear control concept, the Sliding Mode Control is employed as a learning strategy, in which the neural network is considered as a control process and computes the stable and dynamic learning rates of neural network. By considering the unknown faults approximation and reconstruction, this online learning strategy shows a rapid sensor fault detection, approximation, and reconstruction with high preciseness and rapidness compared to conventional strategy and algorithms presented in literature. Approaches used in literature do not have much higher preciseness and fast response to fault occurrence compared to the strategy proposed in this study. In second strategy, the neural network controller strategy is proposed with concept of filtered error scheme. Online weight updating strategy comprise of additional term to back-propagation, plus an additional robustifying term, assures the stability and rapid convergence of the faulty system. The stability analysis of the proposed fault tolerance control is also provided. While considering stability of system, this robust online adaptive fault tolerance control shows a fast convergence in the presence of unknown disturbances and faults. The robust adaptive neural controller is compared with the conventional gradient descent based controller in the existence of various sensor faults and failures. The proposed strategies are validated on Boeing 747 100/200 aircraft, results show the efficiency, preciseness and robustness of strategies compared to the algorithm presented in literature.

Appendices

Appendix A

Proof of Lemma 1

Two-Norm concept is used in this proof. From Eq. (48), $\left\| {N^{ - 1} (t,t - \delta )} \right\| \le 1/\beta_{1}$, it also indicates that for any constant term $\beta_{3}$

$$ \int_{t - \delta }^{t} {\left\| {C(\tau )} \right\|}^{2} d\tau < \beta_{3} $$

(78)

And

$$ \begin{aligned} \int_{t - \delta }^{t} {\left\| {C(\tau )} \right\|} d\tau &= \left\langle {\left\| C \right\|,1} \right\rangle \le \left\| {\left\| C \right\|} \right\| \cdot \left\| 1 \right\| \hfill \\ &= \left[ {\int_{t - \delta }^{t} {\left\| {C(\tau )} \right\|^{2} d\tau } } \right]^{1/2} \left[ {\int_{t - \delta }^{t} {1d\tau } } \right]^{1/2} \le \beta_{3}^{1/2} \delta^{1/2} \hfill \\ \end{aligned} $$

(79)

The state trajectory is defined as;

$$ x(t) = x(t_{0} ) + \int_{{t_{0} }}^{t} {B(\tau )u(\tau )} d\tau $$

(80)

By using the standard methods relating to adjoint operator in C(t), the initial conditions can be found in terms of u(t) and y(t) in finite limit, when it is determined then for all t and with $\delta$, the limited constant in Eq. (48)

$$ \begin{aligned} x(t) &= N^{ - 1} (t,t - \delta )\int_{t - \delta }^{t} {C^{T} (\tau )} Y(\tau )d\tau \hfill \\ & \quad + N^{ - 1} (t,t - \delta )\int_{t - \delta }^{t} {C^{T} (\lambda )} C(\lambda )\int_{t - \delta }^{t} {B(\tau )} u(\tau )d\tau d\lambda \hfill \\ & \equiv x_{1} (t) + x_{2} (t) \hfill \\ \end{aligned} $$

(81)

Now

$$ \begin{aligned} \left\| {x_{1} (t)} \right\| &\le \left\| {N^{ - 1} (t,t - \delta )} \right\|\left\| {\int_{t - \delta }^{t} {C^{T} (\tau )y(\tau )d\tau } } \right\| \hfill \\ & \le \frac{1}{{\beta_{1} }}\int_{t - \delta }^{t} {\left\| {C(\tau )} \right\|} \left\| {y(\tau )} \right\|d\tau \hfill \\ & \le \frac{Y}{{\beta_{1} }}\int_{t - \delta }^{t} {\left\| {C(\tau )} \right\|} d\tau \le \frac{{Y(\delta \beta_{3} )^{1/2} }}{{\beta_{1} }} \hfill \\ \end{aligned} $$

(82)

With Y an upper bound on $\left\| {y(t)} \right\|$ which is finite as $y(t) \in L_{\infty } p$ and for the second term,

$$ \begin{aligned} \left\| {x_{2} (t)} \right\| &\le \frac{1}{{\beta_{1} }}\int_{t - \delta }^{T} {\left\| {C^{T} (\lambda )C(\lambda )} \right\|} \int_{\lambda }^{t} {\left\| {B(\tau )u(\tau )} \right\|} d\tau d\lambda \hfill \\ & \le \frac{1}{{\beta_{1} }}\int_{t - \delta }^{t} {\left\| {C^{T} (\lambda )C(\lambda )} \right\|} \int_{t - \delta }^{t} {\left\| {B(\tau )u(\tau )} \right\|} d\tau d\lambda \hfill \\ & \le \frac{1}{{\beta_{1} }}\int_{t - \delta }^{T} {\left\| {C(\lambda )} \right\|^{2} } d\lambda \int_{t - \delta }^{t} {\left\| {B(\tau )} \right\|} \left\| {u(\tau )} \right\|d\tau \hfill \\ &\le \frac{{\beta_{3} }}{{\beta_{1} }}\beta_{4} \delta U \hfill \\ \end{aligned} $$

(83)

With U an upper bound on $\left\| {u(t)} \right\|$ and $\beta_{4}$ an upper bound on $\left\| {B(t)} \right\|$ both assuring finite as $u(t) \in L_{\infty }^{m} .B(t) \in L_{\infty }^{n \times m} .$

Appendix B

Proof of Lemma 1

Assume that $\mathop {\lim }\nolimits_{t \to \infty } \dot{f}\left( t \right) \ne 0$. Then, $\exists \varepsilon > 0$ and a monotone increasing sequence $\left\{ {t_{n} } \right\}$ such that $t_{n} \to \infty$ as $n \to \infty$ and $\left| {\dot{f}\left( {t_{n} } \right)} \right| \ge \varepsilon$ for all $n \in N.$

Since $\dot{f}\left( t \right)$ is uniformly continuous, for such $\varepsilon$, $\exists \delta > 0$ such that $\forall n \in N$

$$ \left| {t - t_{n} } \right| < \delta \Rightarrow \left| {\dot{f}(t) - \dot{f}(t_{n} )} \right| \le \frac{\varepsilon }{2} $$

(84)

Therefore, if $t \in \left[ {t_{n} , t_{n} + \delta } \right]$, then

$$ \begin{aligned} \left| {\dot{f}(t)} \right| &= \left| {\dot{f}(t_{n} ) - (\dot{f}(t_{n} ) - \dot{f}(t))} \right| \hfill \\ & \ge \left| {\dot{f}(t_{n} )} \right| - \left| {\dot{f}(t_{n} ) - \dot{f}(t)} \right| \hfill \\ & \ge \varepsilon - \frac{\varepsilon }{2} \hfill \\ & = \frac{\varepsilon }{2} \hfill \\ \end{aligned} $$

(85)

Since $f\left( t \right) \in C^{1}$, we have

$$ \begin{aligned} \left| {\int_{a}^{{t_{n} + \delta }} {\dot{f}(t)dt - } \int_{a}^{{t_{n} }} {\dot{f}(t)dt} } \right| &= \left| {\int_{{t_{n} }}^{{t_{n} + \delta }} {\dot{f}(t)dt} } \right| \hfill \\ & \ge \int_{{t_{n} }}^{{t_{n} + \delta }} {\left| {\dot{f}(t)} \right|} dt \hfill \\ & \ge \int_{{t_{n} }}^{{t_{n} + \delta }} {\frac{\varepsilon }{2}dt} \hfill \\ & = \frac{\varepsilon \delta }{2} > 0 \, \hfill \\ \end{aligned} $$

(86)

However

$$ \begin{aligned} \mathop {\lim }\limits_{t \to \infty } \left| {\int_{a}^{{t_{n} + \delta }} {\dot{f}(t)dt - \int_{a}^{{t_{n} }} {\dot{f}(t)dt} } } \right| &= \mathop {\lim }\limits_{t \to \infty } \left| {f(t_{n} + \delta ) - f(t_{n} )} \right| \hfill \\ &= \mathop {\lim }\limits_{t \to \infty } \left| {f(t_{n} + \delta )} \right| - \mathop {\lim }\limits_{t \to \infty } \left| {f(t_{n} )} \right| \hfill \\ & = \left| \alpha \right| - \left| \alpha \right| = 0 \hfill \\ \end{aligned} $$

(87)

Therefore $\mathop {\lim }\nolimits_{t \to \infty } \dot{f}\left( t \right) = 0$.

Appendix C

Parameter	Definition
$K_{v}$	Positive definite constant gain matrix
$\tau$	Control input
$v$	Robustifying term
$s$	Sliding mode surface
$M$	Positive definite skew-symmetric matrix
$\varepsilon_{N}$	Tacking error
$b_{d}$	Positive constant
$\gamma$	Small positive value
$\alpha_{1} ,\alpha_{2} ,\beta_{1} ,\beta_{2} ,\delta$	Positive constant parameters
$M$	Mass properties
$C$	Structural nonlinear terms
$K$	Stiffness matrix
$R$	Aerodynamic matrix
$\varphi \left( . \right)$	Neural network activation function
$w$	NN weight parameter
ƞ	NN learning rate parameter
$\hat{w}$	Adaptive NN weight parameter
$I$	Moment of inertia matrix
$\varLambda$	Symmetric positive definite matrix
$T_{s}$	Step size