A multi-objective stochastic model for a reverse logistics supply chain design with environmental considerations

Abstract

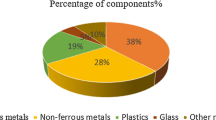
Some electronic devices have a short lifetime, and variety-seeking and consumerism are increasingly growing in today’s societies. Moreover, electronic wastes contain precious substances such as gold, silver, copper, and aluminum. The proper disposal and processing of them by recycling offer considerable advantages to the environment, given the hazardous natures of such devices’ substances. The proposed reverse logistics with waste electrical and electronic equipment (WEEE) is an important task considered by researchers, the use of which offers economic benefits and reduces the environmental impacts of wastes. The present study models the electrical and electronic equipment (EEE) reverse logistics process as a bi-objective mixed-integer programming model under uncertainties. The mathematical model investigates two objectives: an economic objective and an environmental objective. The first is minimizing cost, while the second is maximizing the environmental score by reverse logistics processes in recovering and recycling. The parameters of demand and WEEE return rate which is obtained from the customer were considered as two uncertain parameters. A scenario-based stochastic programming (SSP) approach is applied to deal with the uncertainties. A case study of an electronic equipment manufacturer in Esfahan, Iran was included. The model was solved by a nominal approach and an SSP approach via the epsilon-constraint (EC) and augmented epsilon-constraint (AEC) methods to obtain optimal Pareto solutions and compare the methods. Finally, the optimal results of the two approaches were evaluated. The results indicated that the SSP approach using the AEC method had better outcomes.

Appendix

1.1 Introducing the symbols of a certain model

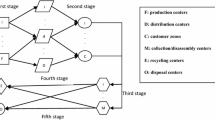
Sets

J: set of product {1, 2, …, J}.

U: set of raw materials {1, 2, …, U}.

${B}_{j}$: set of raw materials required to produce the product j.

S: set of supplier {1, 2, …, S}.

P: set of fixed points of production centers {1, 2, …, P}.

D: set of fixed points of distribution/redistribution center {1, 2, …, D}.

C: set of customer centers {1, 2, …, C}.

I: set of potential points of collection/inspection centers {1, 2, …, I}.

R: set of potential points of recovery centers {1, 2, …, R}.

K: set of fixed points of disassembly centers {1, 2, …, K}.

L: set of fixed points of disposal centers {1, 2, …, L}.

M: set of fixed points of secondary market {1, 2, …, M}.

N: set of potential points of recycling centers {1, 2, …, N}.

Parameters

${tc}_{s\to p}^{u}$: the cost of carrying a unit of material u from supplier s to the production center p.

${tc}_{p\to d}^{j}$: the cost of carrying a unit of product j from production p to the distribution center d.

${tc}_{d\to c}^{j}$: the cost of carrying a unit of product j from distribution center d to the customer centers c.

${tcr}_{c\to i}^{j}$: the cost of carrying a unit of returning product j from the customer center c to the collection/inspection center i.

${tcr}_{i\to r}^{j}$: the cost of carrying a unit of returning product j from the collection/inspection center i to the recovery center r.

${tcr}_{r\to d}^{j}$: the cost of carrying a unit of returning product j from the recovery center r to the distribution center d.

${tcr}_{i\to k}^{j}$: the cost of carrying a unit of returning product j from the collection/inspection center i to the disassembly center k.

${tcr}_{k\to l}^{u}$: the cost of carrying a unit of returning material u from the disassembly center k to the disposal center l.

${tcr}_{k\to n}^{u}$: the cost of carrying a unit of returning material u from the disassembly center k to the recycling center n.

${tcr}_{n\to l}^{u}$: the cost of carrying a unit of returning material u from the recycling center n to the disposal center l.

${tcr}_{n\to m}^{u}$: the cost of carrying a unit of returning material u from the recycling center n to the secondary market m.

${req}_{ju}$: the required quantity of the row material u for the production of a product j.

${cp}_{j}$: the cost of producing a unit of product j.

${cj}_{j}$: the cost of separating a unit of product j.

${ca}_{u}$: the cost of destroying a unit of raw material u.

${fci}_{i}$: fixed cost for the construction of a collection/inspection center i.

${fcr}_{r}$: fixed cost for the construction of a recovery center r.

${fcj}_{k}$: fixed cost for the construction of a disassembly center k.

${fcb}_{n}$: fixed cost for the construction of a recovery center n.

${sr}_{j}$: cost savings from product recovery j.

${sb}_{u}$: cost savings from product raw material u.

${capp}_{p}$: the capacity of the production center p.

${capd}_{d}$: capacity of the distribution(redistribution) center d.

${capi}_{i}$: the capacity of the collection/inspection center i.

${capr}_{r}$: the capacity of the recovery center r.

${capj}_{k}$: the capacity of the disassembly center k.

${capa}_{l}$: the capacity of the disposal center l.

${capb}_{n}$: the capacity of the recycling center n.

${capm}_{m}$: the capacity of the secondary market m.

${ezr}_{rj}$: the environmental advantage of a unit of product recovery j in the recovery center r.

${ezb}_{nu}$: the environmental advantage of a unit of material recycling u in the recycling center p.

${d}_{cj}$: customer demand c for product j.

${pc}_{cj}$: percentage of the product j that returns from customer c.

${pr}_{j}$: percentage of the product j can be recovered.

${pb}_{j}$: percentage of the product j can be recycled.

Decision variables

${Q}_{s\to p}^{uj}$: quantity of material u purchased from supplier s to production center p for product j.

${Q}_{p\to d}^{j}$: quantity of product j produced from the production center p to the distribution center d.

${Q}_{d\to c}^{j}$: quantity of product j sent from distribution center d to customer center c.

${Q}_{c\to i}^{j}$: quantity of product returned j from customer center c to collection/inspection center i.

${Q}_{i\to r}^{j}$: quantity of product returned j from collection/inspection center i to recovery center r.

${Q}_{r\to d}^{j}$: quantity of product recovered j from recovery center r to redistribution center d.

${Q}_{i\to k}^{j}$: quantity of product returned j from collection/inspection center i to disassembly center k.

${Q}_{k\to l}^{u}$: quantity of material returned u from the disassembly center k to the disposal center l.

${Q}_{k\to n}^{u}$: quantity of material returned u from the disassembly center k to the recycling center n.

${Q}_{n\to l}^{u}$: quantity of material returned u from the recycling center n to the disposal center l.

${Q}_{n\to m}^{u}$: quantity of material return u from the recycling center n to the secondary market m.

$Q{Q}_{p}^{j}$: production quantity in the production center p.

${w}_{i}$: 1, if a collection/inspection center is located at potential site i and set up; 0, otherwise.

${X}_{r}$: 1, if a recovery center is located at potential site r and set up; 0, otherwise.

${Y}_{k}$: 1, if a disassembly center is located at potential site k and set up; 0, otherwise.

${Z}_{n}$: 1, if a recycling center is located at potential site n and set up; 0, otherwise.

1.2 Introducing the symbols of an uncertain model

An approach used for dealing with uncertainty is to utilize a scenario-based approach. In the proposed problem, uncertainty is considered for two parameters related to demand and a percentage of product that returns from customers. For this purpose, we consider the three states of optimistic, normal and pessimistic. In one approach of two-stage stochastic optimization, decision variables are categorized into two stages (Bozorgi-Amiri et al. 2015):

The first stage variables are those that are considered in the model before uncertainty is included in it (including locating decision variables that must be located in such a way that the locating does not change in scenario occurrence). Second stage variables are those that are added to the model after uncertainty is included (such as allocation decision variables which can be moved according to scenarios if various states of uncertainty parameters occur). The first stage variables in the design stage are determined before the uncertainty parameters. All the sets, parameters, decision variables in the state of the uncertainty model are like before with the difference that the following items are either changed or added.

H: set of possible scenarios {1, 2, …, h}.

Scenario parameters

${d}_{cj}^{h}$: customer demand c for product j in scenario h.

${pc}_{cj}^{h}$: Percentage of the product j that returns from customer c in scenario h.

${\mathrm{P}}_{\mathrm{h}}$: probability of the occurrence in scenario h.

Scenario decision variables

${Q}_{s\to p}^{ujh}$: quantity of material u purchased from supplier s to production center p for product j in scenario h.

${Q}_{p\to d}^{jh}$: quantity of product j produced from the production center p to the distribution center d in scenario h.

${Q}_{d\to c}^{jh}$: quantity of product j sent from distribution center d to customer center c in scenario h.

${Q}_{c\to i}^{jh}$: quantity of product returned j from the customer center c to collection/inspection center i in scenario h.

${Q}_{i\to r}^{jh}$: quantity of product returned j from collection/inspection center i to recovery center r in scenario h.

${Q}_{r\to d}^{jh}$ quantity of product recovered j from recovery center r to redistribution center d in scenario h.

${Q}_{i\to k}^{jh}$: quantity of product returned j from collection/inspection center i to disassembly center k in scenario h.

${Q}_{k\to l}^{uh}$: quantity of material returned u from the disassembly center k to the disposal center l in scenario h.

${Q}_{k\to n}^{uh}$: quantity of material returned u from the disassembly center k to the recycling center n in scenario h.

${Q}_{n\to l}^{uh}$: quantity of material returned u from the recycling center n to the disposal center l in scenario h.

${Q}_{n\to m}^{uh}$: quantity of material return u from the recycling center n to the secondary market m in scenario h.

$Q{Q}_{p}^{jh}$: production quantity in the production center p in scenario h.

In the following, the data of the problem under consideration studied are stated.