Modeling and optimizing a multi-period closed-loop supply chain for pricing, warranty period, and quality management

Abstract

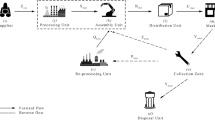
Nowadays, most of the researchers have focused on collecting the used products to carry out the recovery process. This paper deals with the repair process to improve the virtual age of used products and integrate to forward flow as a closed-loop supply chain (CLSC). The products can be returned to the chain several times until they have the required quality to be repaired. Here the optimal number of returning and repairing the used products for maximization of the profits are calculated. Also, the price of selling the products, the acquisition cost, and the warranty period are determined to motivate the customers to bring back their used products and increase the demand for products. For our proposed multi-period problem, an appropriate inventory control policy is taken, and in case of increasing the production amount, additional capacity can be installed by extra cost. The proposed mixed-integer non-linear model has been solved by three metaheuristic algorithms: Particle Swarm Optimization Algorithm (PSO), Genetic Algorithm (GA), Invasive Weeds Optimization algorithm (IWO). Numerical problems depicted model efficiency and by the use of the Taguchi method, qualitative parameters of proposed algorithms are calibrated. Then, the performance comparison of the methods has been done by Relative Performance Deviation.

Appendices

Appendix 1

$${R}_{total}=\sum_{t>1}^{T}\left\{ {\int }_{a-{i}_{t}{x}_{m}}^{b-{i}_{t}{x}_{m}}R\left({v}_{t},x\right)f\left(x\right)dx\right\}$$

$${\varvec{t}}=2$$

$${\varvec{i}}{\varvec{f}} i=1\to R(t=2)={kv}_{1}^{\partial }\frac{{b}^{y+1}-{a}^{y+1}}{(b-a)(y+1)}$$

$${\varvec{t}}=3$$

$${\varvec{i}}{\varvec{f}} i=1\to R\left({i}_{t}\right)={kv}_{1}^{\partial }\frac{{\left(b-{x}_{m}\right)}^{y+1}-{\left(a-{x}_{m}\right)}^{y+1}}{\left(y+1\right)\left(b-a\right)}$$

$${\varvec{i}}{\varvec{f}} i=2\to R\left({i}_{t}\right)={kv}_{2}^{\partial }\frac{{b}^{y+1}-{a}^{y+1}}{(b-a)(y+1)}$$

$${\varvec{t}}=4$$

$${\varvec{i}}{\varvec{f}} i=1\to R\left({i}_{t}\right)={kv}_{1}^{\partial }\frac{{\left(b-{2x}_{m}\right)}^{y+1}-{\left(a-2{x}_{m}\right)}^{y+1}}{\left(y+1\right)\left(b-a\right)}$$

$${\varvec{i}}{\varvec{f}} i=2\to R\left({i}_{t}\right)={kv}_{2}^{\partial }\frac{{\left(b-{x}_{m}\right)}^{y+1}-{\left(a-{x}_{m}\right)}^{y+1}}{\left(y+1\right)\left(b-a\right)}$$

$${\varvec{i}}{\varvec{f}} i=3\to R\left({i}_{t}\right)={kv}_{3}^{\partial }\frac{{b}^{y+1}-{a}^{y+1}}{(b-a)(y+1)}$$

$${{\varvec{i}}}_{{\varvec{t}}}={\varvec{t}}-{\varvec{i}}-1$$

$${R}_{total}=\sum_{t(t>1)}^{T}\left(\sum_{{i}_{t}}^{{I}_{t}} {kv}_{{i}_{t}}^{\partial }\left\{\frac{{(b-{i}_{t}{x}_{m})}^{y+1}-{(a-{i}_{t}{x}_{m})}^{y+1}}{(y+1)(b-a)}\right\}\right)$$

$${R}_{total}=\sum_{t(t>1)}^{T}\left(\sum_{i=1}^{t-i-1\le {I}_{t}} {kv}_{{i}_{t}}^{\partial }\left\{\frac{{(b-(t-i-1){x}_{m})}^{y+1}-{(a-(t-i-1){x}_{m})}^{y+1}}{(y+1)(b-a)}\right\}\right).$$

Appendix 2

In order to solve the model by GAMS software using BARON solver, it should be noted that ${I}_{t}$ is an integer variable and must be transformed into a parameter. For that, we proposed the following procedure:

$$t-i-1\le {I}_{t}+Big{x}_{it} \forall i,t$$

$${kv}_{{i}_{t}}^{\partial }\left\{\frac{{(b-{i}_{t}{x}_{m})}^{y+1}-{(a-{i}_{t}{x}_{m})}^{y+1}}{(y+1)(b-a)}\right\}\le {Big(1- x}_{it}) \forall i,t$$

$${D}_{{i}_{t}}({p}_{r{i}_{t}},w)\left\{C[{\left({i}_{t}{x}_{m}+w\right)}^{\beta }+{i}_{t}^{\beta }{x}_{m}^{\beta }\right\}\le {Big(1- x}_{it}),$$

where ${x}_{it}$ is an auxiliary variable; equals 1 if produced products in period $i$ can be returned and repaired in period $t$.

Appendix 3

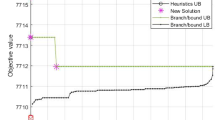
Tables 1, 2 and 3 express the obtained results from implementing ${L}^{9}$, ${L}^{9}$ and ${L}^{27}$ designs GA, PSO and IWO algorithms, respectively.