Skip to main content
Springer Nature Link
Log in

Novel image encryption algorithm using fractional chaos and cellular neural network

  • Original Research
  • Published:
Journal of Ambient Intelligence and Humanized Computing Aims and scope Submit manuscript

Abstract

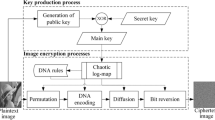
The work presented in this article gives a novel digital image encryption algorithm using a fractional-order chaotic system and cellular neural network. The encryption is done on the lines of chaos-based permutation-substitution architecture. The main contribution lies in key-generation, which is inspired from the Merkel–Damgard scheme. The diffusion mechanism is performed with the help of Conway’s game of life and NARX network. Extensive experimental results of the cipher indicate that the algorithm can withstand classical cryptanalysis and can outperform many other existing image encryption algorithms. Moreover, the scheme fairs pretty well on theoretical aspects of security and passes most of the NIST standards.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Adamatzky A (2010) Game of life cellular automata, vol 1. Springer

  • Arnold V (1978) VI Arnold and A. Avez, ergodic problems of classical mechanics (Benjamin, New York, 1968), p. 20. For quantum-mechanical ergodic problems, see PJM Bongaarts and TH. J. Siskens, Physica (Utrecht) 71, 529 (1978). Physica 71:529

    Google Scholar 

  • Bakhshandeh A, Eslami Z (2013) An authenticated image encryption scheme based on chaotic maps and memory cellular automata. Opt Lasers Eng 51(6):665–673

    Google Scholar 

  • Baptista M (1998) Cryptography with chaos. Phys Lett A 240(1–2):50–54

    MathSciNet  MATH  Google Scholar 

  • Behnia S, Akhshani A, Ahadpour S, Mahmodi H, Akhavan A (2007) A fast chaotic encryption scheme based on piecewise nonlinear chaotic maps. Phys Lett A 366(4–5):391–396

    MATH  Google Scholar 

  • Belazi A, El-Latif AAA, Belghith S (2016) A novel image encryption scheme based on substitution-permutation network and chaos. Signal Process 128:155–170

    Google Scholar 

  • Bhatnagar G, Saha A, Wu QJ, Atrey PK (2014) Analysis and extension of multiresolution singular value decomposition. Inf Sci 277:247–262

    Google Scholar 

  • Chen G, Ueta T (1999) Yet another chaotic attractor. Int J Bifurc Chaos 9(07):1465–1466

    MathSciNet  MATH  Google Scholar 

  • Diethelm K, Ford NJ, Freed AD (2002) A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn 29(1–4):3–22

    MathSciNet  MATH  Google Scholar 

  • Dosselmann R, Yang XD (2011) A comprehensive assessment of the structural similarity index. Signal Image Video Process 5(1):81–91

    Google Scholar 

  • Dua M, Wesanekar A, Gupta V, Bhola M, Dua S (2019) Differential evolution optimization of intertwining logistic map-DNA based image encryption technique. J Ambient Intell Humaniz Comput. https://doi.org/10.1007/s12652-019-01580-z

    Article  Google Scholar 

  • El-Latif AAA, Niu X (2013) A hybrid chaotic system and cyclic elliptic curve for image encryption. AEU Int J Electron Commun 67(2):136–143

    Google Scholar 

  • Elkamchouchi H, Makar M (2005) Measuring encryption quality for bitmap images encrypted with rijndael and kamkar block ciphers. In: Proceedings of the twenty-second national radio science conference, 2005. NRSC 2005. pp 277–284. IEEE

  • François M, Grosges T, Barchiesi D, Erra R (2012) Image encryption algorithm based on a chaotic iterative process. Appl Math 3(12):1910

    Google Scholar 

  • Fridrich J (1998) Symmetric ciphers based on two-dimensional chaotic maps. Int J Bifurc Chaos 8(06):1259–1284

    MathSciNet  MATH  Google Scholar 

  • Gao H, Zhang Y, Liang S, Li D (2006) A new chaotic algorithm for image encryption. Chaos Solitons Fractals 29(2):393–399

    MATH  Google Scholar 

  • Guan Z-H, Huang F, Guan W (2005) Chaos-based image encryption algorithm. Phys Lett A 346(1–3):153–157

    MATH  Google Scholar 

  • Hua Z, Zhou Y, Pun C-M, Chen CP (2015) 2d sine logistic modulation map for image encryption. Inf Sci 297:80–94

    Google Scholar 

  • Kassem A, Hassan HAH, Harkouss Y, Assaf R (2014) Efficient neural chaotic generator for image encryption. Dig Signal Process 25:266–274

    Google Scholar 

  • Katz J, Lindell Y (2014) Introduction to modern cryptography. CRC Press

  • Li C, Peng G (2004) Chaos in Chen’s system with a fractional order. Chaos Solitons Fractals 22(2):443–450

    MathSciNet  MATH  Google Scholar 

  • Li X, Li C, Lee I-K (2016) Chaotic image encryption using pseudo-random masks and pixel mapping. Signal Process 125:48–63

    Google Scholar 

  • Li Y, Wang C, Chen H (2017) A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt Lasers Eng 90:238–246

    Google Scholar 

  • Liu H, Wang X (2011) Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Optics Commun 284(16–17):3895–3903

    Google Scholar 

  • Liu H, Wang X et al (2012) Image encryption using DNA complementary rule and chaotic maps. Appl Soft Comput 12(5):1457–1466

    Google Scholar 

  • Machicao J, Marco AG, Bruno OM (2012) Chaotic encryption method based on life-like cellular automata. Expert Syst Appl 39(16):12626–12635

    Google Scholar 

  • May RM (2004) Simple mathematical models with very complicated dynamics. In: The theory of chaotic attractors. Springer, pp 85–93

  • Mazloom S, Eftekhari-Moghadam AM (2009) Color image encryption based on coupled nonlinear chaotic map. Chaos Solitons Fractals 42(3):1745–1754

    MATH  Google Scholar 

  • Merkle R (1979) Secrecy, authentication, and public key systems. Ph. D. Thesis, Stanford University

  • Musanna F, Kumar S (2018) A novel fractional order chaos-based image encryption using fisher yates algorithm and 3-d cat map. Multimed Tools Appl. https://doi.org/10.1007/s11042-018-6827-2

    Article  Google Scholar 

  • Musanna F, Kumar S (2020) A novel image encryption algorithm using chaotic compressive sensing and nonlinear exponential function. J Inf Secur Appl 54:102560

    Google Scholar 

  • Musanna F, Dangwal D, Kumar S, Malik V (2020) A chaos-based image encryption algorithm based on multiresolution singular value decomposition and a symmetric attractor. Imaging Sci J. https://doi.org/10.1080/13682199.2020.1732116

  • Norouzi B, Mirzakuchaki S (2017) An image encryption algorithm based on DNA sequence operations and cellular neural network. Multimed Tools Appl 76(11):13681–13701

    Google Scholar 

  • Pak C, Huang L (2017) A new color image encryption using combination of the 1d chaotic map. Signal Process 138:129–137

    Google Scholar 

  • Pareek N, Patidar V, Sud K (2005) Cryptography using multiple one-dimensional chaotic maps. Commun Nonlinear Sci Numer Simul 10(7):715–723

    MathSciNet  MATH  Google Scholar 

  • Pareek NK, Patidar V, Sud KK (2006) Image encryption using chaotic logistic map. Image Vis Comput 24(9):926–934

    Google Scholar 

  • Pareek NK, Patidar V, Sud KK (2013) Diffusion-substitution based gray image encryption scheme. Dig Signal Process 23(3):894–901

    MathSciNet  Google Scholar 

  • Rhouma R, Meherzi S, Belghith S (2009) Ocml-based colour image encryption. Chaos Solitons Fractals 40(1):309–318

    MATH  Google Scholar 

  • Rukhin A, Soto J, Nechvatal J, Smid M, Barker E (2001) A statistical test suite for random and pseudorandom number generators for cryptographic applications. Technical report, Booz-Allen and Hamilton Inc Mclean Va

  • Shaheen AM, Sheltami TR, Al-Kharoubi TM, Shakshuki E (2019) Digital image encryption techniques for wireless sensor networks using image transformation methods: DCT and DWT. J Ambient Intell Humaniz Comput 10(12):4733–4750

    Google Scholar 

  • Shannon CE (1948) A mathematical theory of communication. Bell Syst Tech J 27(3):379–423

    MathSciNet  MATH  Google Scholar 

  • Suri S, Vijay R (2019) A synchronous intertwining logistic map-DNA approach for color image encryption. J Ambient Intell Humaniz Comput 10(6):2277–2290

    Google Scholar 

  • Tong X, Cui M (2008) Image encryption with compound chaotic sequence cipher shifting dynamically. Image Vis Comput 26(6):843–850

    Google Scholar 

  • Usama M, Khan MK, Alghathbar K, Lee C (2010) Chaos-based secure satellite imagery cryptosystem. Comput Math Appl 60(2):326–337

    MathSciNet  MATH  Google Scholar 

  • Wang Z, Bovik AC, Sheikh HR, Simoncelli EP et al (2004) Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 13(4):600–612

    Google Scholar 

  • Wang X-Y, Yang L, Liu R, Kadir A (2010) A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn 62(3):615–621

    MathSciNet  MATH  Google Scholar 

  • Wang Y, Wong K-W, Liao X, Chen G (2011) A new chaos-based fast image encryption algorithm. Appl Soft Comput 11(1):514–522

    Google Scholar 

  • Wang X, Liu L, Zhang Y (2015) A novel chaotic block image encryption algorithm based on dynamic random growth technique. Opt Lasers Eng 66:10–18

    Google Scholar 

  • Wang X, Feng L, Zhao H (2019) Fast image encryption algorithm based on parallel computing system. Inf Sci 486:340–358

    MATH  Google Scholar 

  • Wolf A, Swift JB, Swinney HL, Vastano JA (1985) Determining Lyapunov exponents from a time series. Phys D Nonlinear Phenom 16(3):285–317

    MathSciNet  MATH  Google Scholar 

  • Wu Y, Noonan JP, Agaian S et al (2011) NPCR and UACI randomness tests for image encryption. Cyber J Multidiscip J Sci Technol J Sel Areas Telecommun JSAT 1(2):31–38

    Google Scholar 

  • Xiang T, Liao X, Tang G, Chen Y, Wong K-W (2006) A novel block cryptosystem based on iterating a chaotic map. Phys Lett A 349(1–4):109–115

    MATH  Google Scholar 

  • Yang H, Wong K-W, Liao X, Zhang W, Wei P (2010) A fast image encryption and authentication scheme based on chaotic maps. Commun Nonlinear Sci Numer Simul 15(11):3507–3517

    MATH  Google Scholar 

  • Zahmoul R, Ejbali R, Zaied M (2017) Image encryption based on new beta chaotic maps. Opt Lasers Eng 96:39–49

    Google Scholar 

  • Zhang Q, Guo L, Wei X (2010) Image encryption using DNA addition combining with chaotic maps. Math Comput Model 52(11–12):2028–2035

    MathSciNet  MATH  Google Scholar 

  • Zhang Y-Q, Wang X-Y (2014) A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice. Inf Sci 273:329–351

    Google Scholar 

  • Zhang Y-Q, Wang X-Y (2015) A new image encryption algorithm based on non-adjacent coupled map lattices. Appl Soft Comput 26:10–20

    Google Scholar 

  • Zhen W, Xia H, Ning L, Xiao-Na S (2012) Image encryption based on a delayed fractional-order chaotic logistic system. Chin Phys B 21(5):050506

    Google Scholar 

  • Zhu C (2012) A novel image encryption scheme based on improved hyperchaotic sequences. Opt Commun 285(1):29–37

    Google Scholar 

  • Zhu Z-L, Zhang W, Wong K-W, Yu H (2011) A chaos-based symmetric image encryption scheme using a bit-level permutation. Inf Sci 181(6):1171–1186

    Google Scholar 

Download references

Acknowledgements

One of the authors, Farhan Musanna, with grant number MHR-01-23-200-428 is grateful to Ministry of Human Resource Development (MHRD), Government of India and Indian Institute of Technology Roorkee, for providing financial aid for this work. Further, this work is also partially supported by the project grant no. CRG/2020/002040 of SERB New Delhi, India.

Author information

Authors and Affiliations

  1. Department of Mathematics, IIT Roorkee, Roorkee, India

    Farhan Musanna, Deepak Dangwal & Sanjeev Kumar

Authors
  1. Farhan Musanna
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Deepak Dangwal
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Sanjeev Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Sanjeev Kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Musanna, F., Dangwal, D. & Kumar, S. Novel image encryption algorithm using fractional chaos and cellular neural network. J Ambient Intell Human Comput 13, 2205–2226 (2022). https://doi.org/10.1007/s12652-021-02982-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12652-021-02982-8