Abstract
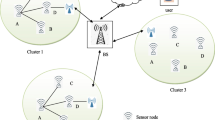
In wireless sensor networks (WSNs), mutual coordination of cluster heads (CHs) is essential to transmit their data towards the sink node through many-hop fashion. As a result of this activity, the CHs in close vicinity to the BS are overburdened with massive relay traffic, which establishes a hot-spot problem. In this paper, in order to capture the hot-spot problem, harris hawk optimization (HHO) based algorithms have been proposed, jointly termed as HHO-UCRA (HHO build on unequal clustering and routing algorithms). In the first step, CH selection mechanism has been proposed based on HHO based technique. Afterwards, the derived CH_Assignment function is used for the cluster formation. Finally, efficient hawk encoding schemes and novel fitness functions of HHO based technique have been formulated for both the algorithms. In the extensive simulation, HHO-UCRA is executed with varying number of sensors and CHs for all the WSN scenarios. Thereafter, the proposed algorithm is evaluated with some recent existing routing approaches and standard meta-heuristic based approach known as PSO-UCRA, to show the efficiency in terms of benchmark indicators of WSNs, such as network energy consumption, lifetime of network, convergence rate, data packets received by the BS and the number of alive nodes.








Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Abbasi AA, Younis M (2007) A survey on clustering algorithms for wireless sensor networks. Comput Commun 30(14–15):2826–2841
Afsar MM, Tayarani-N MH (2014) Clustering in sensor networks: a literature survey. J Netw Comput Appl 46:198–226
Afsar MM, Younis M (2014) An energy-and proximity-based unequal clustering algorithm for wireless sensor networks. In: 39th annual IEEE conference on local computer networks. IEEE, pp 262–269
Akkaya K, Younis M (2005) A survey on routing protocols for wireless sensor networks. Ad Hoc Netw 3(3):325–349
Akyildiz IF, Su W, Sankarasubramaniam Y, Cayirci E (2002) Wireless sensor networks: a survey. Comput Netw 38(4):393–422
Bagci H, Yazici A (2013) An energy aware fuzzy approach to unequal clustering in wireless sensor networks. Appl Soft Comput 13(4):1741–1749
Balakrishna S, Thirumaran M, Solanki VK, Núñez VER et al (2020) Incremental hierarchical clustering driven automatic annotations for unifying iot streaming data. Int J Interact Multimed Artif Intell 6(2):56–70
Banka H, Jana PK et al (2016) Pso-based multiple-sink placement algorithm for protracting the lifetime of wireless sensor networks. In: Proceedings of the second international conference on computer and communication technologies. Springer, pp 605–616
Bara’a AA, Khalil EA (2012) A new evolutionary based routing protocol for clustered heterogeneous wireless sensor networks. Appl Soft Comput 12(7):1950–1957
Carrabs F, Cerulli R, Gentili M, Raiconi A et al (2015) Maximizing lifetime in wireless sensor networks with multiple sensor families. Comput Oper Res 60:121–137
Carrabs F, Cerulli R, Raiconi A et al (2015) A hybrid exact approach for maximizing lifetime in sensor networks with complete and partial coverage constraints. J Netw Comput Appl 58:12–22
Carrabs F, Cerulli R, D’Ambrosio C, Raiconi A (2016) Extending lifetime through partial coverage and roles allocation in connectivity-constrained sensor networks. IFAC-PapersOnLine 49(12):973–978
Carrabs F, Cerulli R, D’Ambrosio C, Raiconi A (2017) Prolonging lifetime in wireless sensor networks with interference constraints. In: International conference on green, pervasive, and cloud computing. Springer, pp 285–297
Dietrich I, Dressler F (2009) On the lifetime of wireless sensor networks. ACM Trans Sens Netw (TOSN) 5(1):1–39
Guru SM, Halgamuge SK, Fernando S (2005) Particle swarm optimisers for cluster formation in wireless sensor networks. In: 2005 international conference on intelligent sensors, sensor networks and information processing. IEEE, pp 319–324
Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H (2019) Harris hawks optimization: algorithm and applications. Future Gener Comput Syst 97:849–872
Heinzelman Wendi B, Chandrakasan AP, Balakrishnan H (2002) An application-specific protocol architecture for wireless microsensor networks. IEEE Trans Wirel Commun 1(4):660–670
Heinzelman WR, Chandrakasan A, Balakrishnan H (2000) Energy-efficient communication protocol for wireless microsensor networks. In: Proceedings of the 33rd annual Hawaii international conference on system sciences. IEEE, p 10
Jain A, Khari M, Verdú E, Omatsu S, Crespo RG (2020) A route selection approach for variable data transmission in wireless sensor networks. Cluster Comput 23(3):1697–1709
Jiang C-J, Shi W-R, Tang X-L et al (2010) Energy-balanced unequal clustering protocol for wireless sensor networks. J China Univ Posts Telecommun 17(4):94–99
Khalil EA, Bara’a AA (2011) Energy-aware evolutionary routing protocol for dynamic clustering of wireless sensor networks. Swarm Evolut Comput 1(4):195–203
Kumar S, Solanki VK, Choudhary SK, Selamat A, González CR (2020) Comparative study on ant colony optimization (ACO) and k-means clustering approaches for jobs scheduling and energy optimization model in internet of things (IoT). Int J Interact Multimed Artif Intell 6(1):107–116
Lalwani P, Banka H, Kumar C (2017) Crwo: clustering and routing in wireless sensor networks using optics inspired optimization. Peer-to-Peer Netw Appl 10(3):453–471
Le-Ngoc KK, Tho QT, Bui TH, Rahmani AM, Hosseinzadeh M (2021) Optimized fuzzy clustering in wireless sensor networks using improved squirrel search algorithm. Fuzzy Sets Syst. https://doi.org/10.1016/j.fss.2021.07.018
Lee S, Choe H, Park B, Song Y, Kim C (2011) Luca: an energy-efficient unequal clustering algorithm using location information for wireless sensor networks. Wirel Pers Commun 56(4):715–731
Lindsey S, Raghavendra CS (2002) Pegasis: power-efficient gathering in sensor information systems. In: Proceedings, IEEE aerospace conference, vol 3. IEEE, p 3
Liu T, Li Q, Liang P (2012) An energy-balancing clustering approach for gradient-based routing in wireless sensor networks. Comput Commun 35(17):2150–2161
Malathi L, Gnanamurthy RK, Chandrasekaran K (2015) Energy efficient data collection through hybrid unequal clustering for wireless sensor networks. Comput Electr Eng 48:358–370
Pasupathi S, Shanmuganthan V, Robinson H, Khari M, Verdú E, Gonzalez CR (2021) Energy efficiency maximization algorithm for underwater mobile sensor networks. Earth Sci Inform IP:1–25. https://doi.org/10.1007/s12145-020-00478-1 (03)
Rao PCS, Banka H (2017a) Energy efficient clustering algorithms for wireless sensor networks: novel chemical reaction optimization approach. Wirel Netw 23(2):433–452
Rao PCS, Banka H (2017) Novel chemical reaction optimization based unequal clustering and routing algorithms for wireless sensor networks. Wirel Netw 23(3):759–778
Rao PCS, Banka H, Jana PK (2015) A gravitational search algorithm for energy efficient multi-sink placement in wireless sensor networks. In: International conference on swarm, evolutionary, and memetic computing. Springer, pp 222–234
Sabor N, Abo-Zahhad M, Sasaki S, Ahmed SM (2016) An unequal multi-hop balanced immune clustering protocol for wireless sensor networks. Appl Soft Comput 43:372–389
Saxena S, Mehta D (2021) An adaptive fuzzy-based clustering and bio-inspired energy efficient hierarchical routing protocol for wireless sensor networks. Wirel Pers Commun 120:2887–2906
Song MAO, Zhao C-L (2011) Unequal clustering algorithm for wsn based on fuzzy logic and improved aco. J China Univ Posts Telecommun 18(6):89–97
Soro S, Heinzelman WB (2005) Prolonging the lifetime of wireless sensor networks via unequal clustering. In: 19th IEEE international parallel and distributed processing symposium. IEEE, p 8
Xiao Y, Yin H, Zhang Y, Qi H, Zhang Y, Liu Z (2021) A dual-stage attention-based conv-lstm network for spatio-temporal correlation and multivariate time series prediction. Int J Intell Syst 36(5):2036–2057
Jiuqiang X, Liu W, Lang F, Zhang Y, Wang C (2010) Distance measurement model based on rssi in wsn. Wirel Sens Netw 2(8):606
Younis O, Fahmy S (2004) Heed: a hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. IEEE Trans Mob Comput 3(4):366–379
Jiguo Yu, Qi Y, Wang G, Guo Q, Xin G (2011) An energy-aware distributed unequal clustering protocol for wireless sensor networks. Int J Distrib Sens Netw 7(1):202145
Zeng B, Dong Y (2016) An improved harmony search based energy-efficient routing algorithm for wireless sensor networks. Appl Soft Comput 41:135–147
Zhang J, Yin J, Tianyi X, Gao Z, Qi H, Yin H (2020) The optimal game model of energy consumption for nodes cooperation in wsn. J Ambient Intell Humaniz Comput 11(2):589–599
Author information
Authors and Affiliations
Contributions
List of author’s contribution as follows. (1) HHO obtained better results in various benchmark function as compare to other optimization techniques, therefore, HHO has been adopted to address the clustering and routing issue for the first time and have been obtained better results. (2) Efficient Encoding scheme has been designed for representing the solution for clustering and routing problems. (3) A Novel cluster formation function has been designed for the efficient formation of clusters.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Harris hawks optimization (HHO)
Appendix 1: Harris hawks optimization (HHO)
In the swarm intelligence optimization algorithm group, harris hawks optimization is one of the recent innovation, which is developed by Heidari et al. It is framed using the hunting strategy of hawks birds. Harris hawks shows the smart behavior while attacking the prey. They starts from monitoring the prey and ends after successfully attacking the prey. In this process, each hawk knows the position of other group members by the help of which hunting process can be executed.
HHO is composed of two phases. First one is diversification and another is intensification. Both the phases together mimics the hunting strategy of prey. First phase also consists of two sub-phases: (1) diversification and (2) process of switching from diversification to intensification. Intensification phase is based on various strategy, namely, (1) soft besiege, (2) hard besiege, (3) soft besiege with progressive quick pounce and (4) hard besiege with progressive quick pounce. Among all these strategies, one of them is taken into the consideration dynamically according to the situation. The detail description of both the phases are as follows.
1.1 1.1: Diversification
In this process, basic nature of harris hawks (HH) is considered, they keep an eye on desert site to track and detect a prey. In order to detect the prey, harris hawks perch on random locations, it is found on two strategies. In the first strategy, perch depends on the other family members and position of rabbit, which is shown in Eq. 29 when \(d<0.5\). In the second strategy, harris hawks are sitting in random tall trees for the perching, which is shown in Eq. 29 when \(d\ge 0.5\).
where \(\partial (t+1)\) represents the position of hawks in the next generation, \(\partial _{rabbit}\) is position of rabbit, \(\partial (t)\) denotes the current generation vector, various random numbers generated between 0 and 1 is denoted by \(r_1\), \(r_2\), \(r_3\), \(r_4\) and d, randomly chosen hawk is represented by \(\partial _{rand}\), and upper and lower bound of variable is shown by LB and UB. The average locations of hawks is represented by \(\partial _m(t)\).
1.2 1.2: Switching from diversification to intensification
Initially, optimization techniques explore the search space i.e., diversification. Thereafter, exploits the neighborhood of the solution (intensification). This phenomena is modeled in HHO using the escaping energy (E) of prey (rabbit). If \(|E|\ge 1\) then diversification is performed, when \(|E|<1\) intensification is taken into the consideration. Hence, switch from diversification to intensification is performed using the escaping energy or prey. The estimation of energy is shown in Eq. 31.
1.3 Intensification
This process is composed of four strategies, namely, (a) soft besiege, (b) hard besiege, (c) soft besiege with progressive quick pounce and (d) hard besiege with progressive quick bounce. The detail description of all these strategies are as follows.
(a) Soft Besiege: In the soft besiege, prey have enough energy to escape, but, failure to escape. This phenomena is modeled using the Eq. 32, when \(r\ge 0.5\) and \(|E| \ge 0.5\).
where \(r_5\) is a random number between 0 and 1, and J represents the jump strength.
(b) Hard Besiege: In the hard besiege, prey/rabbit is not having enough energy to escape and hawk performs the surprise pounce on it. This scenario is modeled using the Eq. 35, when \(r\ge 0.5\) and \(|E| < 0.5\).
(c) soft Besiege Strategy with Progressive Quick Pounce: In this strategy, prey has sufficient amount of energy to escape and still soft besiege is modeled over it. This case is more intelligent than the aforementioned case, when \(|E|\ge\) and \(r< 0.5\). This scenario is modeled using the levy flight function, which is shown in Eq. 36.
Here, Y decides the hawks next movement, which can be estimated as follows.
When hawk approaching towards the prey, then prey and hawk both sometimes perform random movement. This pattern is modeled using LF function as follows.
where u, v are random number between 0 and 1, and \(\omega\) is a constant value.
(d) Hard Besiege: Strategy with Progressive Quick Pounce In this strategy, prey not having sufficient energy to escape and hard besiege is modeled over it, when \(|E|<0.5\) and \(r<0.5\). This scenario is represented using the Eq. 40.
The estimation of Y and Z values are as follows.
Illustration of figure 9: The preliminary phase of harris hawk optimization is Identification (to generate random solutions i.e r1, r2, r3, r4) which have been shown in Fig. 9a. In this phase, the hawk identifies its target and its vicinity. The next step can have two outcomes to proceed which depends upon the energy of prey \(E_r\). If \(E_r\) is greater than equal to one, then firstly diversification phase (exploration) takes place where the hawks exhausts the prey leaving with very low energy is shown in Fig. 9b, followed by intensification (exploitation) phase which is shown in Fig. 9c. But, if initially the energy of prey \(E_r\) is less than one, then directly intensification takes place. In the Intensification phase there are four possibilities of strategies which take place namely, soft besiege strategy (SBS), hard besiege strategy (HBS), soft besiege and progressive quick pounce strategy and hard besiege and progressive quick pounce strategy which are shown in Fig. 9d–g respectively. All of these strategies have been discussed briefly in Sect. 2. The final outcome depends upon the chance of prey to escape (r). If r is smaller than 0.5 then the prey escapes successfully and if the value of r is greater than or equal to 0.5 then the prey cannot escape.
Rights and permissions
About this article
Cite this article
Jain, D., Shukla, P.K. & Varma, S. Energy efficient architecture for mitigating the hot-spot problem in wireless sensor networks. J Ambient Intell Human Comput 14, 10587–10604 (2023). https://doi.org/10.1007/s12652-022-03711-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12652-022-03711-5