A robust possibilistic optimization model for organ transplantation network design considering climate change and organ quality

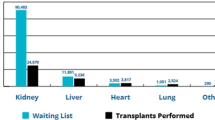
Abstract

In healthcare supply chain management particularly in emergency facilities, organ transplantation network plays a significant task. Donor hospital location and organ allocation can be essential aspects of the transplant network. In the allocation decisions area, weather conditions, quality of organs, and types of vehicles lead to life-challenging issues for the organ recipient. Due to the lack of studies covering location-allocation and organ transplant network design problems concerning uncertain conditions with climate change, quality of organs, and different types of vehicles, this paper proposes a new multi-objective mixed-integer non-linear programming (MINLP) model. The organ transplant network model aims to minimize the network cost and time and to maximize the quality of transmitted organs regarding economic and social dimensions simultaneously. Also, a new hybrid solution approach is presented based on robust possibilistic and ABS-compromise programming methods to handle uncertainties. The developed MINLP model is proper for adapting the design in a multi-organ transplant supply chain that employs multiple donations to deal with fluctuations of organs demands, climate change and organ quality in the supply. The hybrid solution procedure is investigated in an application example from the literature, referring to the organ transplant supply chain, which is exclusively vulnerable to such risks. The outcomes show that by employing the proposed approach, the objective functions increase 35.5%, 74.1%, and 19%, respectively. Also, the results indicate that utilizing the risk of climate change raises the total cost by 1.3% compared to operating without this condition. Furthermore, the time increases 2.3% by considering the risk of climate change in this network. The sensitivity and comparative analyses determine that the quality of the organ enhances 17.8% by increasing the range of the ischemia time from 5 to 55 h.

Appendices

Appendix A

1.1 The review of the literature

Table 6 presents a comprehensive literature review on organ transplant network design in the supply chain.

Table 6 Classification of reviewed papers

Appendix B

2.1 Percentage of transportation risk

See Table 7.

Table 7 Percentage of transport risk in different climate conditions

Appendix C

3.1 Possibility distribution

The possibility distribution is shown in Fig. 8.

Fig. 8

Trapezoidal possibility distribution

3.2 Linearization process of the robust optimization model

To linearize Eqs. (94), (96), and (97) that have positive and binary variables, the following methods are used. In Eq. (61), ${\rho }_{ikov}^{t}$ is a positive variable and θ is a binary variable. When these two variables are multiplied, this equation changes to a non-linear position. For linearization, ${\kappa }_{ikov}^{t}$ is used the following equations:

$$ \kappa_{ikov}^{t} \le M.\rho_{ikov}^{t} ,\quad \forall i,k,o,v,t $$

$$ \kappa_{ikov}^{t} \le \theta ,\quad \forall i,k,o,v,t $$

$$ \kappa_{ikov}^{t} \ge \theta - M\left( {1 - \rho_{ikov}^{t} } \right) ,\quad \forall i,k,o,v,t $$

$$ \mathop \sum \limits_{t}^{T} t.\rho_{ikov}^{t} sp_{v} \left( 3 \right) - \kappa_{ikov}^{t} sp_{v} \left( 3 \right) + \kappa_{ikov}^{t} sp_{v} \left( 4 \right) \le \mathop \sum \limits_{t}^{T} t.d_{ik} \alpha_{ikov}^{t} ,\quad \forall i,k,o,v $$

For the linearization of Eq. (96) that non-linear terms exist in a fraction of equation, $Q_{o}$ is used.

$$ \begin{gathered} \left( {\left( {1 - \theta } \right)ISC_{o} \left( 4 \right) + \theta ISC_{o} \left( 3 \right)} \right) - \mathop \sum \limits_{i}^{I} \mathop \sum \limits_{k}^{K} \mathop \sum \limits_{t}^{T} t.\rho_{ikov}^{t} - \mathop \sum \limits_{i}^{I} \mathop \sum \limits_{k}^{K} \mathop \sum \limits_{t}^{T} t.\alpha_{ikov}^{t} \hfill \\ \ge (\left( {ISC_{o} \left( 3 \right) - ISC_{o} \left( 3 \right)\theta } \right)Q_{o} + \left( {\theta ISC_{o} \left( 4 \right)Q_{o} } \right) ,\quad \forall o,v \hfill \\ \end{gathered} $$

In Eq. (97), multiplication of positive variable ${\Omega }_{ikov}^{t}$ and $\theta$ make a non-linear term. The linear formulation of this equation exists in Eq. (85) and, the linear process exists in the equations below. Also, multiplication of $\theta$ and ${\alpha }_{ikov}^{t}$ is another non-linear term, and the process of linearization exists following equations. For this concept, ${\varrho }_{ikov}$ is a positive variable that is defined by multiplication of ${\Omega }_{ikov}^{t}$ and $\theta$; and ${\varnothing }_{ikov}^{t}$ is proposed for multiplication of $\theta$ and ${\alpha }_{ikov}^{t}$ (Vidal and Goetschalckx 2001).

$${\varrho }_{ikov}\le M.\theta \,\,\forall i,k,o,v$$

$${\varrho }_{ikov}\le M.{\Omega }_{ikov}^{t}\,\,\forall i,k,o,v$$

$${\varrho }_{ikov}\le \theta -M.(1-{\Omega }_{ikov}^{t})\,\,\forall i,k,o,v$$

$${\varnothing }_{ikov}^{t}\le M.{\alpha }_{ikov}^{t}\,\,\forall i,k,o,v,t$$

$${\varnothing }_{ikov}^{t}\le \theta \,\,\forall i,k,o,v,t$$

$${\alpha }_{ikov}^{t}\ge \theta -M.{(1-\alpha }_{ikov}^{t})\,\,\forall i,k,o,v,t$$

$$ \mathop \sum \limits_{i}^{I} \mathop \sum \limits_{k}^{K} \mathop \sum \limits_{o}^{O} \mathop \sum \limits_{v}^{V} \mathop \sum \limits_{t}^{T} {\Omega }_{ikov}^{t} - \varrho_{ikov} ISC_{o} \left( 3 \right) + {\Omega }_{ikov}^{t} ISC_{o} \left( 4 \right) = \mathop \sum \limits_{i}^{I} \mathop \sum \limits_{k}^{K} \mathop \sum \limits_{o}^{O} \mathop \sum \limits_{v}^{V} \mathop \sum \limits_{t}^{T} (((\alpha_{ikov}^{t} - \emptyset_{ikov}^{t} ISC_{o} \left( 3 \right)) + \emptyset_{ikov}^{t} ISC_{o} \left( 4 \right)) - \left( {{\text{t}}.\rho_{ikov}^{t} } \right) + (t.\alpha_{ikov}^{t} )) $$

Appendix D

4.1 Parameters of the application example:

The parameters of the experimental example are determined in Table 8.

Table 8 Parameters of the application example

4.2 Pareto solutions:

See Tables 9, 10, 11.

Table 9 Pareto solution of cost and time

Table 10 Pareto solution of quality and time

Table 11 Pareto solution of quality and cost

4.3 Comparative analysis

See Table 12.

Table 12 Comparisons among several methods' performances