Skip to main content

Advertisement

Springer Nature Link
Log in

Design of a kind of nonlinear neural networks for solving the inverse optimal value problem with convex constraints

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

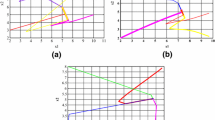
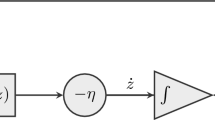
In this paper, we consider how to design a kind of nonlinear neural networks for solving the inverse optimal value problem with convex constraints. Firstly, based on optimal theory, the inverse optimal value problem considered is changed to a class of nonlinear bilevel program problems. Secondly, under the given assumptions, the corresponding nonlinear bilevel programming problem can be reduced to the one-level programming problem. Thirdly, based on the gradient theory, a nonlinear neural network model is designed to solve this one-level programming problem. Moreover, by employing Lyapunov function approach, the proposed neural network is analyzed to be globally Lyapunov stable and capable of generating approximal optimal solution to the inverse optimal value problem. Finally, two illustrative examples are provided to verify the feasibility and the efficiency of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Burton D, Toint Ph.L. (1992) On an instance of the inverse shortest paths problem. Math Program 53:45–61

    Article  MATH  MathSciNet  Google Scholar 

  2. Burton D, Toint Ph L (1994) On the use of an inverse shortest paths algorithm for recovering correlated costs. Math Program 63:1–22

    Article  MATH  MathSciNet  Google Scholar 

  3. Zhang J, Ma Z, Yang C (1995) A column generation method for inverse shortest paths problems. ZOR Math Methods Oper Res 41:347–358

    Article  MATH  MathSciNet  Google Scholar 

  4. Zhang J, Liu Z, Ma Z (1996) On the inverse problem of minimum spanning tree with partition constraints. ZOR Math Methods Oper Res 44:171–188

    Article  MATH  MathSciNet  Google Scholar 

  5. Sokkalingam PT, Ahuja R, Orlin JB (1999) Solving inverse spanning tree problems through network flow techniques. Oper Res 47:291–298

    Article  MATH  MathSciNet  Google Scholar 

  6. Zhang J, Liu Z (1996) Calculating some inverse linear programming problems. J Comput Appl Math 72:261–273

    Article  MATH  MathSciNet  Google Scholar 

  7. Zhang J, Liu Z (1999) A further study on inverse linear programming problems. J Comput Appl Math 106:345–359

    Article  MATH  MathSciNet  Google Scholar 

  8. Yang C, Zhang J, Ma Z (1997) Inverse maximum flow and minimum cut problems. Optimization 40:147–170

    Article  MATH  MathSciNet  Google Scholar 

  9. Zhang J, Cai MC (1998) Inverse problem of minimum cuts. Math Methods Oper Res 47:51-58

    Article  MATH  MathSciNet  Google Scholar 

  10. Ahuja RK, Orlin JB (2001) Inverse optimization. Oper Res 49:771–783

    Article  MATH  MathSciNet  Google Scholar 

  11. Ahuja RK, Orlin JB (2000) A faster algorithm for the inverse spanning tree problem. J Algorithm 34:177–193

    Article  MATH  MathSciNet  Google Scholar 

  12. Ahuja RK, Orlin JB (2002) Combinatorial algorithms for inverse network flow problems. Networks 40:181–187

    Article  MATH  MathSciNet  Google Scholar 

  13. Heuberger C (2004) Inverse combinatorial optimization: a survey on problems, methods, and results. J Comb Optim 8:329–361

    Article  MATH  MathSciNet  Google Scholar 

  14. Ahmed S, Guan Y (2005) The inverse optimal value problem. Math Program 102:91–110

    Article  MATH  MathSciNet  Google Scholar 

  15. Lv YB, Hu TS, Wan ZP (2008) A penalty function method for solving inverse optimal value problem. J Comput Appl Math 220:175–180

    Article  MATH  MathSciNet  Google Scholar 

  16. Lv YB, Chen Z, Wan ZP (2010) A penalty function method based on bilevel programming for solving inverse optimal value problems. Appl Math Lett 23:170–175

    Article  MATH  MathSciNet  Google Scholar 

  17. Lv YB, Chen Z, Wan ZP (2010) A neural network for solving a convex quadratic bilevel programming problem. J Comput Appl Math 234:505–511

    Article  MATH  MathSciNet  Google Scholar 

  18. Tong DL, Mintram R (2010) Genetic Algorithm-Neural Network (GANN): a study of neural network activation functions and depth of genetic algorithm search applied to feature selection. Int J Mach Learn Cybern 1(1-4): 75–87

    Article  Google Scholar 

  19. Boehm O, Hardoon DR, Manevitz LM (2011) Classifying cognitive states of brain activity via one-class neural networks with feature selection by genetic algorithms. Int J Mach Learn Cybern 2(3):125–134

    Article  Google Scholar 

  20. Graaff AJ, Engelbrecht AP (2012) Clustering data in stationary environments with a local network neighborhood artificial immune system. Int J Mach Learn Cybern 3(1):1–26

    Article  Google Scholar 

  21. Sarlin P (2011) Visual tracking of the millennium development goals with a fuzzified self-organizing neural network. Int J Mach Learn Cybern. doi:10.1007/s13042-011-0057-5

  22. Tsang ECC, Wang XZ, Yeung DS (2000) Improving learning accuracy of fuzzy decision trees by hybrid neural networks. IEEE Trans Fuzzy Syst 8 (5): 601–614

    Google Scholar 

  23. Wu H, Wang K, Li N, Wu C, Guo Q, Xu G (2012) Applications of the general nonlinear neural networks in solving the inverse optimal value problem with linear constraints. Inf Technol J 11:713–718

    Article  Google Scholar 

  24. Tarantola A (1987) Inverse problem theory: methods for data fitting and model parameter estimation. Elsevier, Amsterdam, The Netherlands

  25. Wang XJ, Feng SY (1995) The optimality theory of bilevel system. Science Publishers, Beijing

    Google Scholar 

  26. Dempe S (2002) Foundation of bilevel programming. Kluwer Academic Publishers, London

    Google Scholar 

Download references

Acknowledgments

The authors are extremely grateful to the Editor and the Reviewers for their valuable comments and suggestions, which help to enrich the content and improve the presentation of this paper.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Yanshan University, Qinhuangdao, 066001, China

    Huaiqin Wu, Kewang Wang, Qiangqiang Guo, Guohua Xu & Ning Li

Authors
  1. Huaiqin Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Kewang Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Qiangqiang Guo
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Guohua Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Ning Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Huaiqin Wu.

Additional information

This work was supported by the Natural Science Foundation of Hebei Province of China (A2011203103) and the Hebei Province Education Foundation of China (2009157).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wu, H., Wang, K., Guo, Q. et al. Design of a kind of nonlinear neural networks for solving the inverse optimal value problem with convex constraints. Int. J. Mach. Learn. & Cyber. 5, 85–92 (2014). https://doi.org/10.1007/s13042-012-0138-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-012-0138-0

Keywords