Skip to main content

Advertisement

Springer Nature Link
Log in

Novel stability condition of stochastic fuzzy neural networks with Markovian jumping under impulsive perturbations

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

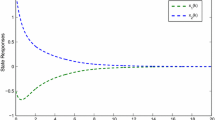
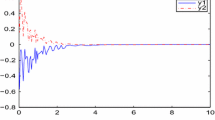
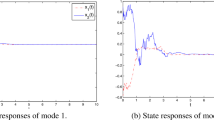
For the first time, this paper investigates the global asymptotic stability of stochastic fuzzy neural networks with mixed delays and Markovian jumping under impulsive perturbations in mean square. The mixed delays include time-varying delay and continuously distributed delay. By using stochastic analysis method, linear convex combination technique, Jensen integral inequality and the free-weight matrix method, a novel sufficient condition is derived to ensure the global asymptotic stability of the equilibrium point of the considered networks in mean square. The proposed result, which is expressed in terms of linear matrix inequalities, can be easily checked via Matlab software. Finally, a numerical example is given to demonstrate the effectiveness and less conservativeness of our theoretical results over existing literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Arnold L (1972) Stochastic differential equations: theory and applications. Wiley, New York

    Google Scholar 

  2. Balasubramaniam P, Vembarasan V (2011) Robust stability of uncertain fuzzy BAM neural networks of neutral-type with Markovian jumping parameters and impulses. Comput Math Appl 62(4):1838–1861

    Article  MathSciNet  MATH  Google Scholar 

  3. Gu K (2000) An integral inequality in the stability problem of time-delay systems. In: Proceedings of 39th IEEE conference decision and control, Sydney, Australia, pp 2805–2810

  4. Haykin S (1994) Neural networks. Prentice-Hall, New Jersey

    MATH  Google Scholar 

  5. Han W, Liu Y, Wang L (2012) Global exponential stability of delayed fuzzy cellular neural networks with Markovian jumping parameters. Neural Comput Appl 21:67–72

    Article  Google Scholar 

  6. He C (2014) Approximation of polygonal fuzzy neural networks in sense of Choquet integral norms. Int J Mach Learn Cyber 5(1):93–99

    Article  Google Scholar 

  7. Li X, Rakkiyappan R, Balasubramaniam P (2011) Existence and global stability analysis of equilibrium of fuzzy cellular neural networks with time delay in the leakage term under impulsive perturbations. J Franklin Inst 348:135–155

    Article  MathSciNet  MATH  Google Scholar 

  8. Lin D, Wang X (2010) Observer-based decentralized fuzzy neural sliding mode control for interconnected unknown chaotic systems via network structure adaptation. Fuzzy Sets Syst 161(15):2066–2080

    Article  MathSciNet  MATH  Google Scholar 

  9. Lin D, Wang X, Nian F, Zhang Y (2010) Dynamic fuzzy neural networks modeling and adaptive backstepping tracking control of uncertain chaotic systems. Neurocomputing 73(16–18):2873–2881

    Article  Google Scholar 

  10. Liu Z, Zhang H, Wang Z (2009) Novel stability criterions of a new fuzzy cellular neural networks with time-varying delays. Neurocomputing 72:1056–1064

    Article  Google Scholar 

  11. Mao X (2002) Exponential stability of stochastic delay interval systems with Markovian switching. IEEE Trans Autom Contr 47(10):1604–1612

    Article  MathSciNet  Google Scholar 

  12. Poznyak AS, Sanchez EN (1995) Nonlinear systems approximation by neural networks: Error stability analysis. Intell Automat Softw Comput Int J 1:247–258

    Article  Google Scholar 

  13. Tang Y, Fang J, Miao Q (2009) On the exponential synchronization of stochastic jumping chaotic neural networks with mixed delays and sector-bounded non-linearities. Neurocomputing 72:1694–1701

    Article  Google Scholar 

  14. Tong S, Li Y, Li Y, Liu Y (2011) Observer-based adaptive fuzzy backstepping control for a class of stochastic nonlinear strict-feedback systems. IEEE Trans Syst Man Cyber B 41(6):1693–1704

    Article  MathSciNet  Google Scholar 

  15. Tong S, Wang T, Li Y, Chen B (2013) A combined backstepping and stochastic small-gain approach to robust adaptive fuzzy output feedback control. IEEE Trans Fuzzy Syst 21(2):314–327

    Article  Google Scholar 

  16. Yang Y, Wang G, Yang Y Parameters optimization of polygonal fuzzy neural networks based on GA-BP hybrid algorithm. Int J Machine Learn Cyber. doi:10.1007/s13042-013-0224-y

  17. Yang T, Yang L (1996) The global stability of fuzzy cellular neural networks. IEEE Trans Circ Syst 43(10):880–883

    Article  Google Scholar 

  18. Yuan C, Lygeros J (2005) Stabilization of a class of stochastic differential equations with Markovian switching. Syst. Control Lett. 54:819–833

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhang Y, Yue D, Tian E (2009) New stability criteria of neural networks with interval time-varying delay: a piecewise delay method. Appl Math Comput 208:249–259

    MathSciNet  MATH  Google Scholar 

  20. Zhou W, Tong D, Gao Y, Ji C, Su H (2012) Mode and delay-dependent adaptive exponential synchronization in \(p\)th moment for stochastic delayed neural networks with Markovian switching. IEEE Trans Neural Netw Learn Syst 23(3):662–668

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Science, Dalian Jiaotong University, 116028, Dalian, People’s Republic of China

    Cheng-De Zheng & Yanli Zhang

  2. School of Information Science and Engineering, Northeastern University, 110004, Shenyang, People’s Republic of China

    Zhanshan Wang

Authors
  1. Cheng-De Zheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yanli Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhanshan Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Cheng-De Zheng.

Additional information

This work was supported by the National Natural Science Foundation of China 61034005, 61074073, 61273022, Program for New Century Excellent Talents in University of China (NCET-10-0306), and the Fundamental Research Funds for the Central Universities under Grants N110504001 and N100104102.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zheng, CD., Zhang, Y. & Wang, Z. Novel stability condition of stochastic fuzzy neural networks with Markovian jumping under impulsive perturbations. Int. J. Mach. Learn. & Cyber. 7, 795–803 (2016). https://doi.org/10.1007/s13042-014-0298-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-014-0298-1

Keywords