Retailer’s optimal strategy for fixed lifetime products

Abstract

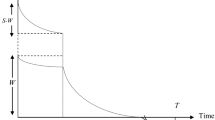
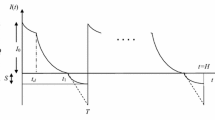
This model illustrates an inventory model to obtain retailer’s optimal replenishment policy for deteriorating items with fixed lifetime, shortages, and time dependent backorder rate. The backorder rate is assumed as a decreasing function of waiting time up to the next replenishment. The aim is to minimize the total relevant cost of the system. The necessary and sufficient conditions are derived analytically. Some lemmas are established for the existence and uniqueness of optimal solution. Finally, some numerical examples, sensitivity analysis, comparison with other models, study of non-considering lifetime of products along with graphical representations are provided to illustrate the proposed model. From the numerical example, this model proves more savings than Wu et al. (Int J Prod Econ 101:369–384, 2006).

Appendices

Appendix A

$$\begin{aligned} \lambda&= {} 1+L-t,\varphi =1+L-t_{d},P=\frac{c_{3}+\delta c_{4}}{\delta }, \phi =\frac{\varphi }{\xi }, \phi _{1}=\frac{\varphi }{\xi _{1}}\\ \eta _{1}&= {} (1+b+bL),\quad \eta _{2}=(6bL^2+12bL-18L+6b-18),\quad \eta _{3}=(9+3b+3bL), \\ \quad \eta _{4}&= {} (3-b-bL),\quad \eta _{5}=(1-b-bL),\quad \eta _{6}=(e^{-bt_{1}}-e^{-bt_{d}}),\quad \eta _{7}=(t_{1}e^{-bt_{1}}-t_{d}e^{-bt_{d}}),\\ \quad \eta _{8}&= {} (2-b-bL),\quad \eta _{9}=(t_{1}^2e^{-bt_{1}}-t_{d}^2e^{-bt_{d}}),\quad \eta _{10}=(1-e^{-bt_{d}})c_{1}+bc_{2}e^{-bt_{d}},\\ \eta _{11}&= {} e^{-bt_{1}}-bt_{1}e^{-bt_{1}},\quad \eta _{12}=1-bt_{1}-e^{-bt_{1}}.\\ \xi&= {} 1+L-t_{1},\xi _{1}=1+L-x, \xi _{2}=(e^{-bx}-e^{-bt_{d}}), \xi _{3}=(xe^{-bx}-t_{d}e^{-bt_{d}}),\\ \xi _{4}&= {} (x^2e^{-bx}-t_{d}^2e^{-bt_{d}}),\xi _{5}=(2xe^{-bx}-bx^2e^{-bx}),\xi _{6}=(e^{-bx}-bxe^{-bx}),\\ \xi _{7}&= {} (-b-bL+bx),\xi _{8}=\frac{c_{1}}{b}(1-e^{-bt_{d}})+c_{2}e^{-bt_{d}},\\ \xi _{9}&= {} -b\eta _{5}e^{-bx}+b\xi _{6}-b^2\xi _{1}(1-bx-e^{-bx})(1+\ln \xi _{1})+b^2\xi _{1} (e^{-bx}-b\xi _{1}-1+bx-e^{-bx}\xi _{7})\ln \xi _{1},\\ \xi _{10}&= {} \frac{\eta _{1}}{b^2\xi _{1}}(\xi _{2}\eta _{5}+b\xi _{1}(b\xi _{1}(1-bx) +\xi _{7}e^{-bx})\ln \xi _{1}+b\xi _{3}),\\ \xi _{11}&= {} \eta _{2}+2\eta _{3}x-12bx^2+6\xi _{1}(\eta _{4}-2bx)+12b\xi _{1}^2\ln \xi _{1}+12\xi _{1} (\eta _{4}-2bx)\ln \xi _{1},\\ \xi _{12}&= {} \frac{b\xi _{8}\varphi }{\xi _{1}}+\frac{(1+bx)\xi _{8}\varphi }{\xi _{1}^2}+ (c_{1}-bc_{2})\left( \eta _{5}e^{-bx}-\xi _{6}+\frac{\eta _{1}\xi _{9}}{b^2\xi _{1}}+\frac{\xi _{10}}{\xi _{1}}\right) ,\\ \xi _{13}&= {} \frac{(1+bx)\xi _{8}\varphi }{\xi _{1}}, \xi _{14}=\xi _{10}-\frac{(\xi _{2}\eta _{5}+b\xi _{3})}{b},\\ \xi _{15}&= {} 1-\frac{\delta (\xi _{13}-c_{2}+(c_{1}-bc_{2})\xi _{14})}{c_{3}+\delta c_{4}} \\ \mu&= {} (t_{1}-t_{d})\eta _{2}+(t_{1}^2-t_{d}^2) \eta _{3}-4b(t_{1}^3-t_{d}^3)-6\xi ^2(\eta _{4}-2bt_{1})\ln \xi +6\varphi ^2(\eta _{4}-2bt_{d})\ln \varphi ,\\ \mu _{1}&= {} (x-t_{d})\eta _{2}+(x^2-t_{d}^2) \eta _{3}-4b(x^3-t_{d}^3)-6\xi _{1}^2(\eta _{4}-2bx)\ln \xi_{1} +6\varphi ^2(\eta _{4}-2bt_{d})\ln \varphi ,\\ \mu _{2}&= {} t_{1}\eta _{2}+t_{1}^2\eta _{3}-4bt_{1}^3-6\xi ^2\ln \xi (\eta _{4}-2bt_{1}) +6\eta _{4}(1+L)^2\ln (1+L),\\ \mu _{3}&= {} (e^{-bt_{1}}-1)\eta _{5}+bt_{1}e^{-bt_{1}}\\ M&= {} \left[ \frac{c_{1}}{b}(1-e^{-bt_{d}})+c_{2}e^{-bt_{d}}\right] \left( \frac{bt_{1}+1}{\xi }\right) \varphi +(c_{1}-bc_{2}) \left[ \frac{1}{b}(\eta _{5}\eta _{6}+b\eta _{7})\left( \frac{\eta _{1}}{b\xi }-1\right) +\xi \eta _{1}\eta _{12}\ln \xi \right] -c_{2}\\ M_{1}&= {} [\frac{c_{1}}{b}(1-e^{-bt_{d}})+c_{2}e^{-bt_{d}}]\left(\frac{bt_{1}+1}{\xi _{1}}\right)\varphi +(c_{1}-bc_{2}) \left[ \frac{1}{b}(\eta _{5}\xi _{2}+b\xi _{3})\left( \frac{\eta _{1}}{b\xi _{1}}-1\right) +\xi _{1}\eta _{1}\ln \xi _{1}(1-bx-e^{-bx})\right] -c_{2}\\ N&= {} \left[ \frac{c_{1}}{b}(1-e^{-bt_{d}})+c_{2}e^{-bt_{d}}\right] (bt_{d}+1)+(c_{1}-bc_{2})\left[ \eta _{1}\xi \ln \xi (1-bt_{d}-e^{-bt_{d}})\right] -c_{2} \end{aligned}$$

Appendix B

$$\begin{aligned} \frac{\partial ^2Z\left( t_{1}^*,T^*\right) }{\partial {t_{1}^*}^2}&= {} \frac{a}{T^*}\Bigg [\frac{\delta P}{[1+\delta (T^*-t_{1}^*)]^2}+\frac{\eta _{10}\varphi }{\xi (t_{1}^*)}+\frac{\eta _{10}(1+bt_{1}^*)\varphi }{b\xi ^2(t_{1}^*)}+(c_{1}-bc_{2})\Bigg \{e^{-bt_{1}^*}\eta _{5}-\eta _{11}(t_{1}^*)\\&\quad+\frac{\eta _{1}}{b\xi (t_{1}^*)}\Big (\eta _{11}(t_{1}^*) -e^{-bt_{1}^*}\eta _{5}-b\xi (t_{1}^*)\eta _{12}(t_{1}^*) \left( 1+\ln \xi (t_{1}^*)\right) -b\xi (t_{1}^*)\ln \xi (t_{1}^*)(\eta _{12}(t_{1}^*)\\&\quad+b\xi (t_{1}^*)(1-e^{-bt_{1}^*}))\Big ) +\eta _{1}\eta _{12}(t_{1}^*)\ln \xi (t_{1}^*)+\frac{\eta _{1}\left[ \eta _{6}(t_{1}^*)\eta _{5}+b\eta _{7}(t_{1}^*)\right] }{b^2\xi ^2(t_{1}^*)}\Bigg \}\Bigg ]\\ \frac{\partial ^2Z\left( t_{1}^*,T^*\right) }{\partial {T^*}^2}&= {} \frac{a\delta P}{T^*\left[ 1+\delta \left( T^*-t_{1}^*\right) \right] ^2}-\frac{2aP\delta \left( T^*-t_{1}^*\right) }{{T^*}^2\left[ 1+\delta \left( T^*-t_{1}^*\right) \right] }+\frac{2a}{{T^*}^3}Z\left( t_{1}^*,T^*\right) \\\\ \frac{\partial Z\left( t_{1}^*,T^*\right) }{\partial t_{1}^*\partial T^*}&= {} -\frac{a\delta P}{T^*\left[ 1+\delta \left( T^*-t_{1}\right) \right] ^2}-\frac{a}{{T^*}^2}\bigg [\left( c_{1}-bc_{2}\right) \bigg \{\left( \frac{\eta _{5}\eta _{6}(t_{1}^*) +b\eta _{7}(t_{1}^*)}{b}\right) \left( \frac{\eta _{1}}{b\xi (t_{1}^*)}-1\right) \\&\quad+ \eta _{1}\eta _{12}(t_{1}^*)\ln \xi (t_{1}^*)\bigg \}+\frac{(1+bt_{1}^*)\varphi }{b\xi (t_{1}^*)}\eta _{10}-\frac{P\delta (T^*-t_{1}^*) }{1+\delta ( T^*-t_{1}^*) }-c_{2}\bigg ] \end{aligned}$$