Skip to main content

Advertisement

Springer Nature Link
Log in

Synchronization of delayed Markovian jump memristive neural networks with reaction–diffusion terms via sampled data control

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

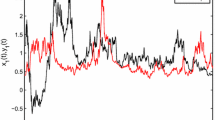
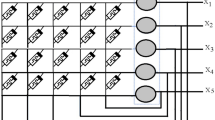
This paper is concerned with the sampled-data synchronization issues for delayed memristive neural networks with Markovian jumping and reaction–diffusion terms. In the frame work of inequality techniques and a useful Lyapunov functional, some new testable algebraic criteria are obtained to ensure the stability of the error system, and thus, the master system can synchronize with the slave system. Finally, an illustrative example is exploited to demonstrate the performance and effectiveness of the developed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Chua L (1971) Memristor—the missing circuit element. IEEE Trans Circuit Theory 18:507–519

    Article  Google Scholar 

  2. Strukov D, Snider G, Stewart D, Williams R (2008) The missing memristor found. Nature 453:80–83

    Article  Google Scholar 

  3. Corinto F, Ascoli A, Gilli M (2011) Nonlinear dynamics of memristor oscillators. IEEE Trans Circuits Syst I 58:1323–1336

    Article  MathSciNet  Google Scholar 

  4. Tour J, He T (2008) Electronics: the fourth element. Nature 453:42–43

    Article  Google Scholar 

  5. Messias M, Nespoli C, Botta V (2010) Hopf bifurcation from lines of equilibria without parameters in memristor oscillators. Int J Bifurcation Chaos 20:437–450

    Article  MATH  MathSciNet  Google Scholar 

  6. Itoh M, Chua L (2008) Memristor oscillators. Int J Bifurcation Chaos 18:3183–3206

    Article  MATH  MathSciNet  Google Scholar 

  7. Petras I (2010) Fractional-order memristor-based Chua’s circuit. IEEE Trans Circuits Syst II Exp Briefs 57:975–979

    Article  Google Scholar 

  8. Tsang E, Wang X, Yeung D (2000) Improving learning accuracy of fuzzy decision trees by hybrid neural networks. IEEE Trans Fuzzy Syst 8:601–614

    Article  Google Scholar 

  9. Wang X, Dong C, Fan T (2007) Training T-S norm neural networks to refine weights for fuzzy if-then rules. Neurocomputing 70:2581–2587

    Article  Google Scholar 

  10. Roska T, Chua L (1992) Cellular neural networks with nonlinear and delay-type tempiate. Int J Circuit Theory Appl 20:469–481

    Article  MATH  Google Scholar 

  11. Li H, Chen B, Zhou Q, Qian W (2009) Robust stability for uncertain delayed fuzzy Hopfield neural networks with Markovian jumping parameters. IEEE Trans Syst Man Cybern B Cybern 39:94–102

    Article  Google Scholar 

  12. Wang Z, Liu Y, Yu L, Liu X (2006) Exponential stability of delayed recurrent neural networks with Markovian jumping parameters. Phys Lett A 356:346–352

    Article  MATH  Google Scholar 

  13. Wu Z, Shi P, Su H, Chu J (2011) Passivity analysis for discrete-time stochastic Markovian jump neural networks with mixed time delays. IEEE Trans Neural Netw 22:1566–1575

    Article  Google Scholar 

  14. Zhang H, Wang Y (2008) Stability analisis of Markovian jumping stochastic Cohen–Grossberg neural networks with mixed time delays. IEEE Trans Neural Netw 19:366–370

    Article  Google Scholar 

  15. Zhu Q, Cao J (2011) Exponential stability of neural networks with both Markovian jump parameters and mixed time delays. IEEE Trans Syst Man Cybern B Cybern 41:341–353

    Google Scholar 

  16. Landsman A, Schwartz I (2007) Complete chaotic synchronization in mutually coupled time-delay systems. Phys Rev E 5:26–33

    Google Scholar 

  17. Huang T, Li C, Liao X (2007) Synchronization of a class of coupled chaotic delays systems with parameter mismatch. Chaos 17:33–121

    Google Scholar 

  18. Cui B, Lou X (2009) Synchronization of chaotic recurrent neural networks with time-varying delays using nonlinear feedback control. Chaos Solitons Fract 39:288–294

    Article  MATH  MathSciNet  Google Scholar 

  19. Gan Q, Xu R, Kang X (2011) Synchronization of chaotic neural networks with mixed time delays. Commun Nonlinear Sci Numer Simul 16:966–974

    Article  MATH  MathSciNet  Google Scholar 

  20. Zhan M, Wei G, Lai C (2002) Transition from intermittency to periodicity in lag synchronization in coupled Rössler oscillators. Phys Rev E 65:36–40

    Article  Google Scholar 

  21. Xu D, Chee C (2002) Controlling the ultimate state of projective synchronization in chaotic systems of arbitrary dimension. Phys Rev E 66:46–50

    Article  Google Scholar 

  22. Li X, Bohner M (2010) Exponential synchronization of chaotic neural networks with mixed delays and impulsive effects via output coupling with delay feedback. Math Comput Model 52:643–653

    Article  MATH  MathSciNet  Google Scholar 

  23. Ding S, Wang Z (2015) Stochastic exponential synchronization control of memristive neural networks with multiple time-varying delays. Neurocomputing 162:16–25

    Article  Google Scholar 

  24. Zhang G, Hu J, Shen Y (2015) Exponential lag synchronization for delayed memristive recurrent neural networks. Neurocomputing 154:86–93

    Article  Google Scholar 

  25. Zhang G, Shen Y (2015) Exponential stabilization of memristor-based chaotic neural networks with time-varying delays via intermittent control. IEEE Trans Neural Netw Learn Syst 26:1431–1441

    Article  Google Scholar 

  26. Bao H, Cao J (2015) Projective synchronization of fractional-order memristor-based neural networks. Neural Netw 63:1–9

    Article  Google Scholar 

  27. Wu A, Wen S, Zeng Z (2012) Synchronization control of a class of memristor-based recurrent neural networks. Inf Sci 183:106–116

    Article  MATH  MathSciNet  Google Scholar 

  28. Fridman E, Seuret A, Richard J (2004) Robust sampled-data stabilization of linear systems: an input delay approach. Automatica 40:1441–1446

    Article  MATH  MathSciNet  Google Scholar 

  29. Boyd S, Ghaoui L, Feron E, Balakrishnan V (1994) Linear matrix inequalities in system and control theory. SIAM, Philadephia

    Book  MATH  Google Scholar 

  30. Lu J (2008) Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos Solitons Fract 35:116–125

    Article  MATH  Google Scholar 

Download references

Acknowledgments

This work was supported by the Scientific and Technological Research Program of Chongqing Municipal Education Commission (Grant No. KJ1501002).

Author information

Authors and Affiliations

  1. Department of Mathematics, and Research Center for Complex Systems and Network Sciences, Southeast University, 210096, Nanjing, China

    Ruoxia Li

  2. Department of Mathematics and Statistics, Chongqing University, 401331, Chongqing, China

    Hongzhi Wei

Authors
  1. Ruoxia Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hongzhi Wei
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ruoxia Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, R., Wei, H. Synchronization of delayed Markovian jump memristive neural networks with reaction–diffusion terms via sampled data control. Int. J. Mach. Learn. & Cyber. 7, 157–169 (2016). https://doi.org/10.1007/s13042-015-0423-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-015-0423-9

Keywords