Skip to main content
Springer Nature Link
Log in

Decomposition methods of formal contexts to construct concept lattices

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

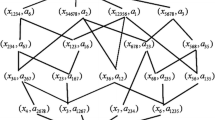
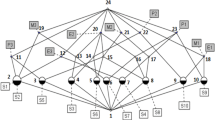
As an important tool for data analysis and knowledge processing, formal concept analysis has been applied to many fields. In this paper, we introduce a decomposition method of a formal context to construct its corresponding concept lattice, which answers an open problem to some extent that how this decomposition method of a context translates into a decomposition method of its corresponding concept lattice. Firstly, based on subcontext, closed relation and pairwise noninclusion covering on the attribute set, we obtain the decomposition theory of a formal context, and then we provide the method and algorithm of constructing the corresponding concept lattice by using this decomposition theory. Moreover, we consider the similar decomposition theory and method of a formal context from the object set. Finally, we make another decomposition of a formal context by combining the above two results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Wang XZ, Xing HJ et al (2015) A study on relationship between generalization abilities and fuzziness of base classifiers in ensemble learning. IEEE Trans Fuzzy Syst 23(5):1638–1654

    Article  Google Scholar 

  2. Wang XZ, Ashfaq RAR, Fu AM (2015) Fuzziness based sample categorization for classifier performance improvement. J Intell Fuzzy Syst 29(3):1185–1196

    Article  MathSciNet  Google Scholar 

  3. Ashfaq RAR., Wang XZ et al (2016) Fuzziness based semi-supervised learning approach for intrusion detection system. Inf Sci. doi:10.1016/j.ins.2016.04.019

  4. Ashfaq RAR, He YL, Chen DG (2016) Toward an efficient fuzziness based instance selection methodology for intrusion detection system. Int J Mach Learn Cybern. doi:10.1007/s13042-016-0557-4

  5. Wille R (1982) Restructuring lattice theory: an approach based on hierarchies of concepts. In: Rival I (ed) Ordered sets. Reidel, Dordrecht-Boston, pp 445–470

    Chapter  Google Scholar 

  6. Ganter B, Wille R (1999) Formal concept analysis: mathematical foundations. Springer-Verlag, Berlin

    Book  MATH  Google Scholar 

  7. Davey BA, Priestley HA (2002) Introduction to lattices and order. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  8. Poelmans J, Ignatov DI, Kuznetsov SO, Dedene G (2013) Formal concept analysis in knowledge processing: a survey on applications. Expert systems with applications 40(16):6538–6560

    Article  Google Scholar 

  9. Kaytoue M, Kuznetsov SO, Napoli A, Duplessis S (2011) Mining gene expression data with pattern structures in formal concept analysis. Inf Sci 181(10):1989–2001

    Article  MathSciNet  Google Scholar 

  10. Codocedo V, Napoli A (2015) Formal concept analysis and information retrieval-a survey. ICFCA 9113:61–77

    MATH  Google Scholar 

  11. Wang XZ (2015) Learning from big data with uncertainty-editorial[J]. J Intell Fuzzy Syst 28(5):2329–2330

    Article  MathSciNet  Google Scholar 

  12. Tonella P (2003) Using a concept lattice of decomposition slices for program understanding and impact analysis. IEEE Trans Softw Eng 29:495–509

    Article  Google Scholar 

  13. Ganapathy V, King D, Jaeger T, Jha S (2007) Mining security sensitive operations in legacy code using concept analysis. In: Proc. 29th Int. conference on software engineering, pp 458–467

  14. Bělohlávek R, Sigmund E, Zacpal J (2011) Evaluation of IPAQ questionnaires supported by formal concept analysis. Inf Sci 181(10):1774–1786

  15. Singh PK, Kumar CA, Gani A (2016) A comprehensive survey on formal concept analysis, its research trends and applications. Int J Appl Math Comput Sci 26(2):495–516

    Article  MathSciNet  MATH  Google Scholar 

  16. Wu WZ, Leung Y, Mi JS (2009) Granular computing and knowledge reduction in formal contexts. IEEE Trans Knowl Data Eng 21(10):1461–1474

    Article  Google Scholar 

  17. Wei L (2005) Reduction theory and approach to rough set and concept lattice. Xi’an Jiaotong University, Xi’an

  18. Shao MW, Leung Y (2014) Relations between granular reduct and dominance reduct in formal contexts. Knowl Based Syst 65:1–11

    Article  Google Scholar 

  19. Dias SM, Vieira NJ (2015) Concept lattices reduction: defnition, analysis and classifcation. Expert Syst Appl 42:7084–7097

    Article  Google Scholar 

  20. Mi JS, Leung Y, Wu WZ (2010) Approaches to attribute reduction in concept lattices induced by axialities. Knowl Based Syst 23:504–511

    Article  Google Scholar 

  21. Ishigure H, Mutoh A, Matsui T, Inuzuka N (2015) Concept lattice reduction using attribute inference. In: IEEE 4th global conference on consumer electronics, Osaka, Japan, pp 108–111

  22. Kumar CA, Dias SM, Vieira NJ (2015) Knowledge reduction in formal contexts using non-negative matrix factorization. Math Comput Simul 109:46–63

    Article  MathSciNet  Google Scholar 

  23. Shao MW, Leung Y, Wu WZ (2014) Rule acquisition and complexity reduction in formal decision contexts. Int J Approx Reason 55:259–274

    Article  MathSciNet  MATH  Google Scholar 

  24. Li JH, Mei CL, Lv YJ (2013) Incomplete decision contexts: approximate concept construction, rule acquisition and knowledge reduction. Int J Approx Reason 54(1):149–165

    Article  MathSciNet  MATH  Google Scholar 

  25. Kumar CA, Srinivas S (2010) Mining associations in healthcare data using formal concept analysis and singular value decomposition. Biol Syst 18(4):787–807

    Article  Google Scholar 

  26. Kumar CA (2012) Fuzzy clustering based formal concept analysis for association rules mining. Appl Artif Intell 26(3):274–301

    Article  Google Scholar 

  27. Wang LD, Liu XD (2008) Concept analysis via rough set and AFS algebra. Inf Sci 178:4125–4137

    Article  MathSciNet  MATH  Google Scholar 

  28. Wan Q, Wei L (2015) Approximate concepts acquisition based on formal contexts. Knowl Based Syst 75:78–86

    Article  Google Scholar 

  29. Singh PK, Kumar ChA, Li JH (2015) Concepts reduction in formal concept analysis with fuzzy setting using Shannon entropy. Int J Mach Learn Cybern 6(1):1–11

    Article  Google Scholar 

  30. Bělohlávek R (2000) Similarity relations in concept lattices. Logic Comput 10:823–845

  31. Yao YY (2008) Probabilistic rough set approximations. Int J Approx Reason 49:255–271

    Article  MATH  Google Scholar 

  32. Xu WH, Li WT (2016) Granular computing approach to two way learning based on formal concept analysis in fuzzy datasets. IEEE Trans Cybern 46(2):366–379

    Article  Google Scholar 

  33. Li JH, Mei CL, Xu WH, Qian YH (2015) Concept learning via granular computing: a cognitive viewpoint. Inf Sci 298:447–467

    Article  MathSciNet  Google Scholar 

  34. Li JH, Ren Y, Mei CL, Qian YH, Yang XB (2016) A comparative study of multigranulation rough sets and concept lattices via rule acquisition. Knowl Based Syst 91:152–164

    Article  Google Scholar 

  35. Li KW, Shao MW, Wu WZ (2016) A data reduction method in formal fuzzy contexts. Int J Mach Learn Cybern. doi:10.1007/s13042-015-0485-8

  36. Li MZ, Wang GY (2015) Knowledge reduction in crisply generated fuzzy concept lattices. Fundam Inf 142(1–4):307–335

    Article  MathSciNet  MATH  Google Scholar 

  37. Cornejo ME, Medina J, Eloisa R (2015) Cuts or thresholds, what is the best reduction method in fuzzy formal concept analysis? Fuzzy Systems (FUZZ-IEEE). In: 2015 IEEE international conference on Istanbul. doi:10.1109/FUZZ-IEEE.2015.7337990

  38. Yao YY (2016) Rough-set concept analysis: interpreting RS-definable concepts based on ideas from formal concept analysis. Inf Sci 346–347:442–462

    Article  MathSciNet  Google Scholar 

  39. Zhi HL, Li JH (2016) Granule description based on formal concept analysis. Knowl Based Syst 104:62–73

    Article  Google Scholar 

  40. Li JH, Huang CC, Qi JJ, Qian YH, Liu WQ (2016) Three-way cognitive concept learning via multi-granularity. Inf Sci. doi:10.1016/j.ins.2016.04.051

  41. Yao YY (2012) An outline of a theory of three-way decisions. Rough Set and Knowledge Technology, Spring International Publishing: volume 7413 of Lecture Notes in Computer Science, pp 1–17

  42. Qi JJ, Wei L, Yao YY (2014) Three-way formal concept analysis. rough set and knowledge technology. In: Lecture notes in computer science, vol 8818. Spring International Publishing, pp 732–741

  43. Bělohlávek R, Vychodil V (2010) Discovery of optimal factors in binary data via a novel method of matrix decomposition. J Comput Syst Sci 76:3–20

  44. Outrata J, Vychodil V (2012) Fast algorithm for computing fixpoints of Galois connections induced by object-attribute relational data. Inf Sci 185:114–127

    Article  MathSciNet  MATH  Google Scholar 

  45. Zou L, Zhang Z, Long J (2015) A fast incremental algorithm for constructing concept lattices. Expert Syst Appl 42:4474–4481

    Article  Google Scholar 

  46. Qian T, Wei L (2014) A novel concept acquisition approach based on formal contexts. Sci World J 1:1–7

    Article  Google Scholar 

  47. Krajca P, Outrata J, Vychodil V (2010) Parallel algorithm for computing fixpoints of Galois connections. Ann Math Artif Intell 59(2):257–272

    Article  MathSciNet  MATH  Google Scholar 

  48. Kourie DG, Obiedkov S, Watson BW, Vander MD (2009) An incremental algorithm to construct a lattice of set intersections. Sci Comput Program 74:128–142

    Article  MathSciNet  MATH  Google Scholar 

  49. Qi JJ, Wei L, Li ZZ (2005) A partitional view of concept lattice. In: Rough set, fuzzy set, data mining, and granular computing. Lecture notes in computer science, vol 3641. Spring, Berlin, pp 74–83

  50. Qi JJ, Liu W, Wei L (2012) Computing the set of concepts through the composition and decomposition of formal contexts. Int Conf Mach Learn Cybern 4:1326–1332

    Google Scholar 

Download references

Acknowledgments

This work is partially supported by the National Natural Science Foundation of China (Grant Nos. 11371014 and 11071281), the Natural Science Basic Research Plan in Shaanxi Province of China (Program No. 2014JM8306) and the State Scholarship Fund of China.

Author information

Authors and Affiliations

  1. School of Mathematics, Northwest University, Xi’an, 710069, China

    Ting Qian & Ling Wei

  2. College of Science, Xi’an Shiyou University, Xi’an, 710065, China

    Ting Qian

  3. School of Computer Science and Technology, Xidian University, Xi’an, 710071, China

    Jianjun Qi

Authors
  1. Ting Qian
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ling Wei
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jianjun Qi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ling Wei.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qian, T., Wei, L. & Qi, J. Decomposition methods of formal contexts to construct concept lattices. Int. J. Mach. Learn. & Cyber. 8, 95–108 (2017). https://doi.org/10.1007/s13042-016-0578-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-016-0578-z

Keywords