Skip to main content

Advertisement

Springer Nature Link
Log in

Bifurcation control in the delayed fractional competitive web-site model with incommensurate-order

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

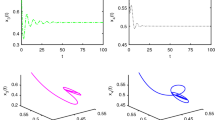
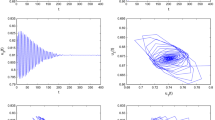
The delayed competitive web-site system with incommensurate fractional orders, based on the Lotka–Volterra competition model, is firstly proposed in this paper. It is demonstrated that there is a stability switch for time delay, Hopf bifurcation occurs when time delay crosses through a critical value and each order has important influence on the creation of bifurcation. Furthermore, a nonlinear delayed feedback control is successfully designed to postpone the onset of Hopf bifurcation, extend the stability domain, and then the system possesses the stability in a larger parameter range. Finally, numerical simulations are included to illustrate the efficiency of the obtained theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Strom D (1977) The best of push. Datamation 43(4):56–61

    Google Scholar 

  2. Adamic LA, Huberman BA (2000) The nature of markets in the world wide web. Q J Electron Commence 1:5–12

    Google Scholar 

  3. Maurer SM, Huberman BA (2003) Competitive dynamics of web sites. J Econ Dyn Control 27:2195–2206

    Article  MathSciNet  MATH  Google Scholar 

  4. Ren Y, Yang D, Diao X (2010) Websites competition model with market segmentation and its stability analysis. J Dalian Univ Technol 50(5):816–821

    MathSciNet  Google Scholar 

  5. Cabo RM, Gimeno R (2013) Estimating population ecology models for the WWW market: evidence of competitive oligopolies. Nonlinear Dyn Psychol Life Sci 17(1):159–172

    Google Scholar 

  6. Aluja M, Ordano M, Guillen L, Rul J (2015) Understanding long-term fruit fly (Diptera: Tephritidae) population dynamics: implications for areawide management. J Econ Entomol 105(3):823–836

    Article  Google Scholar 

  7. Li J, Zhao A (2015) Stability analysis of a non-autonomous Lotka–Volterra competition model with seasonal succession. Appl Math Model 40(2):763–781

    Article  MathSciNet  Google Scholar 

  8. Avelino PP, Bazeia D, Menezes J (2014) String networks in [formula omitted] Lotka–Volterra competition models. Phys Lett A 378(4):393–397

    Article  MATH  Google Scholar 

  9. Jia Y, Wu J, Xu HK (2014) Positive solutions of a Lotka–Volterra competition model with cross-diffusion. Comput Math Appl 68(10):1220–1228

    Article  MathSciNet  MATH  Google Scholar 

  10. Caputo M (1967) Linear models of dissipation whose Q is almost frequency independent-II. Geophys J R Astron Soc 13:529–539

    Article  Google Scholar 

  11. Kvitsinskii AA (1993) Fractional integrals and derivatives: theory and applications. Teoret Mat Fiz 3:397–414

    Google Scholar 

  12. Sun HH, Abdelwahab AA, Onaral B (1984) Linear approximation of transfer function with a pole of fractional order. IEEE Trans Autom Control 29:441–444

    Article  MATH  Google Scholar 

  13. Podlubny I (1999) Fractional differential equations. Academic Press, New York

    MATH  Google Scholar 

  14. Mandelbrot BB (1982) The fractal geometry of nature. Henry Holt and Company, New York

    MATH  Google Scholar 

  15. Rakkiyappan R, Cao JD, Velmurugan G (2015) Existence and uniform stability analysis of fractional-order complex-valued neural networks with time delays. IEEE Trans Neural Netw Learn Syst 1(26):84–97

    Article  MathSciNet  MATH  Google Scholar 

  16. Liu H, Li S, Wang H, Huo Y, Luo J (2015) Adaptive synchronization for a class of uncertain fractional-order neural networks. Entropy 17(10):7185–7200

    Article  MathSciNet  Google Scholar 

  17. Li G, Liu H (2016) Stability analysis and synchronization for a class of fractional-order neural networks. Entropy 18(2):55

    Article  Google Scholar 

  18. Xiao M, Zheng WX, Jiang GP, Cao JD (2015) Undamped oscillations generated by hopf bifurcations in fractional-order recurrent neural networks with caputo derivative. IEEE Trans Neural Netw Learn Syst 26(12):3201–3214

    Article  MathSciNet  Google Scholar 

  19. Cao JD, Xiao M (2007) Stability and Hopf bifurcation in a simplified BAM neural network with two time delays. IEEE Trans Neural Netw 18:416–430

    Article  Google Scholar 

  20. Yu P (2004) Bifurcation dynamics in control systems. Bifurc Control 293(3):719–722

    Google Scholar 

  21. Abed EH, Fu JH (1987) Local feedback stabilization and bifurcation control: II. Stationary bifurcation. Syst Control Lett 8:467–473

    Article  MathSciNet  MATH  Google Scholar 

  22. Chen GR, Moiola JL, Wang HO (2000) Bifurcation control: theories, methods and applications. Int J Bifurc Chaos 10:511–548

    MathSciNet  MATH  Google Scholar 

  23. Yu P, Chen G (2004) Hopf bifurcation control using nonlinear feedback with polynomial functions. Int J Bifurc Chaos 14:1683–1704

    Article  MathSciNet  MATH  Google Scholar 

  24. Pan Y, Yu H, Er MJ (2014) Adaptive neural pd control with semiglobal asymptotic stabilization guarantee. IEEE Trans Neural Netw Learn Syst 25(12):2264–2274

    Article  Google Scholar 

  25. Pan Y, Liu Y, Xu B, Yu H (2016) Hybrid feedback feedforward: an efficient design of adaptive neural network control. Neural Netw 76:122–134

    Article  Google Scholar 

  26. Pan Y, Yu H (2016) Composite learning from adaptive dynamic surface control. IEEE Trans Autom Control 61(9):2603–2609

    Article  MathSciNet  MATH  Google Scholar 

  27. Xiao M, Ho DWC, Cao JD (2009) Time-delayed feedback control of dynamical small-world networks at Hopf bifurcation. Nonlinear Dyn 58:319–344

    Article  MathSciNet  MATH  Google Scholar 

  28. Shi M, Wang ZH (2013) Stability and Hopf bifurcation control of a fractional-order small world network model. Sci China Phys Mech 43(4):467–477

    Google Scholar 

  29. Min X, Cao J (2006) Stability and Hopf bifurcation in a delayed competitive web sites model. Phys Lett A 353(2–3):138–150

    MATH  Google Scholar 

  30. Deng W, Li C, Lu J (2007) Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn 48(4):409–416

    Article  MathSciNet  MATH  Google Scholar 

  31. Zhang JL, Dou JH, Shi Y (2011) Hopf bifurcation of a competitive web-site system with reflexive and competition delays. Pure Appl Math 27:51–54

    MathSciNet  MATH  Google Scholar 

  32. Xu CJ, Wu YS (2015) Frequency domain analysis for Hopf bifurcation in a delayed competitive web-site model. Int J Comput Inf Sci Engine 9(2):138–141

    Google Scholar 

  33. Huang CD, Cao JD, Xiao M (2016) Hybrid control on bifurcation for a delayed fractional gene regulatory network. Chaos Solitons Fract 87:19–29

    Article  MathSciNet  MATH  Google Scholar 

  34. Wang H, Yu Y, Wen G, Zhang S, Yu J (2015) Global stability analysis of fractional-order Hopfield neural networks with time delay. Neurocomputing 154(C):15–23

    Article  Google Scholar 

  35. Abdelouahab MS, Hamri NE, Wang J (2012) Hopf bifurcation and chaos in fractional-order modified hybrid optical system. Nonlinear Dyn 69(1–2):275–284

    Article  MathSciNet  MATH  Google Scholar 

  36. Lozi RP, Abdelouahab MS (2015) Hopf Bifurcation and chaos in simplest fractional-order memristor-based electrical circuit. Indian J Ind Appl Math 6(2):105–119

    Article  Google Scholar 

  37. Padula F, Alcantara S, Vilanova R, Visioli A (2013) \(H_\infty\)control of fractional linear systems. Automatica 49:2276–2280

    Article  MathSciNet  MATH  Google Scholar 

  38. Bhalekar S, Varsha D (2011) A predictor–corrector scheme for solving nonlinear delay differential equations of fractional order. J Fract Calc Appl 1(5):1–9

    Google Scholar 

Download references

Acknowledgements

This work was jointly supported by the National Natural Science Foundation of China under Grant nos. 61573096, 61272530 and 61573194, the National Science Foundational of Jiangsu Province of China under Grant no. BK2012741, the “333 Engineering” Foundation of Jiangsu Province of China under Grant no. BRA2015286.

Author information

Authors and Affiliations

  1. School of Information Engineering, Nanjing Xiaozhuang University, Nanjing, 211171, China

    Lingzhi Zhao

  2. Research Center for Complex Systems and Network Sciences, and School of Mathematics, Southeast University, Nanjing, 210096, China

    Jinde Cao

  3. Nonlinear Analysis and Applied Mathematics Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, 21589, Saudi Arabia

    Jinde Cao, Ahmed Alsaedi & Bashir Ahmad

  4. School of Mathematics and Computer Science, Hubei University of Arts and Science, Xiangyang, 441053, China

    Chengdai Huang

  5. College of Automation, Nanjing University of Posts and Telecommunications, Nanjing, 210003, China

    Min Xiao

Authors
  1. Lingzhi Zhao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jinde Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Chengdai Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Min Xiao
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Ahmed Alsaedi
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Bashir Ahmad
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Lingzhi Zhao.

Appendix

Appendix

1.1 Appendix A

$$\begin{aligned} \mathfrak {M}_1&=-\alpha x^*\omega _0^{q_2+q_3+1}\sin \frac{(q_2+q_3)\pi }{2}-\alpha ^2{(x^*)}^2 \left(\omega _0^{q_2+1}\sin \frac{q_2\pi }{2}+\omega _0^{q_3+1}\sin \frac{q_3\pi }{2}\right),\\ \mathfrak {M}_2&=\omega _0\alpha ^3{(x^*)}^3-\omega _0\alpha \gamma ^2{(x^*)}^3+\alpha x^*\omega _0^{q_2+q_3+1}\cos \frac{(q_2+q_3)\pi }{2}\\&\quad+\alpha ^2{(x^*)}^2\left(\omega _0^{q_2+1}\cos \frac{q_2\pi }{2}+\omega _0^{q_3+1} \cos \frac{q_3\pi }{2}\right),\\ \mathfrak {N}_1&=\alpha x^*(q_2+q_3)\omega _0^{q_2+q_3-1}\cos \frac{(q_2+q_3-1)\pi }{2}\\&\quad+\alpha ^2{(x^*)}^2\left[q_2\omega _0^{q_2-1}\cos \frac{(q_2-1)\pi }{2} +q_3\omega _0^{q_3-1}\cos \frac{(q_3-1)\pi }{2}\right]\\&\quad-\tau _0\left[\alpha ^3{(x^*)}^3-\alpha \gamma ^2{(x^*)}^3+\alpha x^*\omega _0^{q_2+q_3}\cos \frac{(q_2+q_3)\pi }{2}\right.\\ &\quad\left.+\alpha ^2{(x^*)}^2\left(\omega _0^{q_2}\cos \frac{q_2\pi }{2}+\omega _0^{q_3}\cos \frac{q_3\pi }{2}\right)\right] +\left[(q_1+q_2+q_3) \right.\\&\quad\times\omega _0^{q_1+q_2+q_3-1}\cos \frac{(q_1+q_2+q_3-1)\pi }{2}+ \alpha x^*(q_1+q_2)\omega _0^{q_1+q_2-1}\\&\quad\times\cos \frac{(q_1+q_2-1)\pi }{2} +\alpha x^*(q_1+q_3)\omega _0^{q_1+q_3-1} \\&\quad\times\cos \frac{(q_1+q_3-1)\pi }{2}+(\alpha ^2{(x^*)}^2 -\gamma ^2{(x^*)}^2)~q_1\omega _0^{q_1-1} \cos \frac{(q_1-1)\pi }{2}\\&\quad-\gamma ^2{(x^*)}^2 q_2\omega _0^{q_2-1}\cos \frac{(q_2-1)\pi }{2} -\gamma ^2{(x^*)}^2q_3\omega _0^{q_3-1}\\&\quad\left.\times\cos \frac{(q_3-1)\pi }{2})\right]\cos \omega _0\tau _0 -\left[(q_1+q_2+q_3)\omega _0^{q_1+q_2+q_3-1}\sin \frac{(q_1+q_2+q_3-1)\pi }{2}\right.\\&\quad+\alpha x^*(q_1+q_2)\omega _0^{q_1+q_2-1}\sin \frac{(q_1+q_2-1)\pi }{2}+\alpha x^*(q_1+q_3)\omega _0^{q_1+q_3-1}\sin \frac{(q_1+q_3-1)\pi }{2}\\&\quad+(\alpha ^2{(x^*)}^2 -\gamma ^2{(x^*)}^2)~q_1\omega _0^{q_1-1} \sin \frac{(q_1-1)\pi }{2}\\&\quad\left.-\gamma ^2{(x^*)}^2 q_2\omega _0^{q_2-1}\sin \frac{(q_2-1)\pi }{2}-\gamma ^2{(x^*)}^2q_3\omega _0^{q_3-1} \sin \frac{(q_3-1)\pi }{2})\right]\sin \omega _0\tau _0, \end{aligned}$$
$$\begin{aligned} \mathfrak {N}_2&=\alpha x^*(q_2+q_3)\omega _0^{q_2+q_3-1}\sin \frac{(q_2+q_3-1)\pi }{2} +\alpha ^2{(x^*)}^2\left[q_2\omega _0^{q_2-1}\right.\\&\quad\left.\times\sin \frac{(q_2-1)\pi }{2} +q_3\omega _0^{q_3-1}\sin \frac{(q_3-1)\pi }{2}\right]-\tau _0\left[\alpha ^3{(x^*)}^3-\alpha \gamma ^2{(x^*)}^3\right.\\&\quad\left.+\alpha x^*\omega _0^{q_2+q_3}\sin \frac{(q_2+q_3)\pi }{2} +\alpha ^2{(x^*)}^2(\omega _0^{q_2}\sin \frac{q_2\pi }{2}+\omega _0^{q_3} \sin \frac{q_3\pi }{2})\right] +\left[(q_1+q_2+q_3) \right.\\&\quad\times\omega _0^{q_1+q_2+q_3-1}\cos \frac{(q_1+q_2+q_3-1)\pi }{2}+ \alpha x^*(q_1+q_2)\omega _0^{q_1+q_2-1}\\&\quad\times\cos \frac{(q_1+q_2-1)\pi }{2} +\alpha x^*(q_1+q_3)\omega _0^{q_1+q_3-1} \\&\quad\times\cos \frac{(q_1+q_3-1)\pi }{2}+(\alpha ^2{(x^*)}^2-\gamma ^2{(x^*)}^2) ~q_1\omega _0^{q_1-1} \cos \frac{(q_1-1)\pi }{2}\\&\quad-\gamma ^2{(x^*)}^2 q_2\omega _0^{q_2-1}\cos \frac{(q_2-1)\pi }{2} -\gamma ^2{(x^*)}^2q_3\omega _0^{q_3-1}\\&\quad\left.\times\cos \frac{(q_3-1)\pi }{2}\right]\sin \omega _0\tau _0 +\left[(q_1+q_2+q_3)\omega _0^{q_1+q_2+q_3-1}\right.\\&\quad\times\sin \frac{(q_1+q_2+q_3-1)\pi }{2}+\alpha x^*(q_1+q_2)\omega _0^{q_1+q_2-1}\\&\quad\times\sin \frac{(q_1+q_2-1)\pi }{2}+\alpha x^*(q_1+q_3)\omega _0^{q_1+q_3-1}\sin \frac{(q_1+q_3-1)\pi }{2}\\&\quad+(\alpha ^2{(x^*)}^2 -\gamma ^2{(x^*)}^2)~q_1\omega _0^{q_1-1} \sin \frac{(q_1-1)\pi }{2}\\&\quad\left.-\gamma ^2{(x^*)}^2 q_2\omega _0^{q_2-1}\sin \frac{(q_2-1)\pi }{2}-\gamma ^2{(x^*)}^2q_3\omega _0^{q_3-1} \sin \frac{(q_3-1)\pi }{2}\right]\cos \omega _0\tau _0. \end{aligned}$$

1.2 Appendix B

$$\begin{aligned}\mathfrak {M}^*_1&=\omega _0^*(\alpha ^3{x^*}^3-\alpha \gamma ^2{x^*}^3 +k_1\alpha ^2{x^*}^2)+\alpha x^*{(\omega _0^*)}^{q_2+q_3+1}\cos \frac{(q_2+q_3)\pi }{2}\\&\quad+\alpha ^2{(x^*)}^2\left[(\omega _0^*)^{q_2+1}\cos \frac{q_2\pi }{2}+(\omega _0^*)^{q_3+1} \cos \frac{q_3\pi }{2}\right]\\&\quad+k_1\alpha x^*(\omega _0^*)^{q_3+1}\cos \frac{q_3\pi }{2},\\ \mathfrak {M}^*_2&=\alpha x^*(\omega _0^*)^{q_2+q_3+1}\sin \frac{(q_2+q_3)\pi }{2}+\alpha ^2{(x^*)}^2 \left[(\omega _0^*)^{q_2+1}\sin \frac{q_2\pi }{2}\right.\\&\quad\left.+(\omega _0^*)^{q_3+1} \sin \frac{q_3\pi }{2}+k_1\alpha x^*(\omega _0^*)^{q_3+1}\sin \frac{q_3\pi }{2}\right],\\ \mathfrak {N}^*_1&=\alpha x^*(q_2+q_3)(\omega _0^*)^{q_2+q_3-1}\cos \frac{(q_2+q_3-1)\pi }{2} +\alpha ^2{(x^*)}^2\left[q_2(\omega _0^*)^{q_2-1}\right.\\&\quad\left.\times\cos \frac{(q_2-1)\pi }{2} +q_3(\omega _0^*)^{q_3-1}\cos \frac{(q_3-1)\pi }{2}\right] \\&\quad+k_1\alpha x^*q_3(\omega _0^*)^{q_3-1} \cos \frac{(q_3-1)\pi }{2}-\tau _0^*\left[\alpha ^3{(x^*)}^3-\alpha \gamma ^2{(x^*)}^3\right.\\&\quad+\alpha x^*(\omega _0^*)^{q_2+q_3}\cos \frac{(q_2+q_3)\pi }{2} +\alpha ^2{(x^*)}^2\left((\omega _0^*)^{q_2}\cos \frac{q_2\pi }{2}\right.\\&\quad\left.\left.+(\omega _0^*)^{q_3}\cos \frac{q_3\pi }{2}\right) +k_1\alpha x^*(\omega _0^*)^{q_3}\cos \frac{q_3\pi }{2}\right] +\left[(q_1+q_2+q_3)(\omega _0^*)^{q_1+q_2+q_3-1}\right.\\&\quad\times\cos \frac{(q_1+q_2+q_3-1)\pi }{2}+ \alpha x^*(q_1+q_2)\\&\quad\times(\omega _0^*)^{q_1+q_2-1}\cos \frac{(q_1+q_2-1)\pi }{2} +\alpha x^*(q_1+q_3)(\omega _0^*)^{q_1+q_3-1} \cos \frac{(q_1+q_3-1)\pi }{2}\\&\quad+k_1(q_1+q_3)(\omega _0^*)^{q_1+q_3-1} \cos \frac{(q_1+q_3-1)\pi }{2}\\&\quad+(\alpha ^2{(x^*)}^2-\gamma ^2{(x^*)}^2+k_1\alpha x^*)~q_1(\omega _0^*)^{q_1-1} \cos \frac{(q_1-1)\pi }{2}\\&\quad\left.-\gamma ^2{x^*}^2q_2 (\omega _0^*)^{q_2-1}\cos \frac{(q_2-1)\pi }{2 }-\gamma ^2{(x^*)}^2q_3(\omega _0^*)^{q_3-1}\cos \frac{(q_3-1)\pi }{2}\right]\\&\quad\times\cos \omega _0^*\tau _0^*-\left[(q_1+q_2+q_3)(\omega _0^*)^{q_1+q_2+q_3-1} \sin \frac{(q_1+q_2+q_3-1)\pi }{2}\right.\\&\quad+\alpha x^*(q_1+q_2)s^{q_1+q_2-1}\sin \frac{(q_1+q_2-1)\pi }{2}+\alpha x^*(q_1+q_3)\\&\quad\times(\omega _0^*)^{q_1+q_3-1}\sin \frac{(q_1+q_3-1)\pi }{2} +(\alpha ^2{(x^*)}^2-\gamma ^2{(x^*)}^2)~q_1(\omega _0^*)^{q_1-1} \sin \frac{(q_1-1)\pi }{2}\\&\quad-\gamma ^2{(x^*)}^2 q_2(\omega _0^*)^{q_2-1}\sin \frac{(q_2-1)\pi }{2}-\gamma ^2{(x^*)}^2q_3\\&\quad\left.\times(\omega _0^*)^{q_3-1} \sin \frac{(q_3-1)\pi }{2})\right]\sin \omega _0^*\tau _0^*, \end{aligned}$$
$$\begin{aligned} \mathfrak {N}^*_2&=\alpha x^*(q_2+q_3)(\omega _0^*)^{q_2+q_3-1}\sin \frac{(q_2+q_3-1)\pi }{2} +\alpha ^2{(x^*)}^2\left[q_2(\omega _0^*)^{q_2-1}\sin \frac{(q_2-1)\pi }{2} +q_3(\omega _0^*)^{q_3-1}\sin \frac{(q_3-1)\pi }{2}\right]\\ &\quad+k_1\alpha x^*q_3(\omega _0^*)^{q_3-1}\sin \frac{(q_3-1)\pi }{2}-\tau _0^*\left[\alpha ^3{(x^*)}^3 -\alpha \gamma ^2{(x^*)}^3+\alpha x^*(\omega _0^*)^{q_2+q_3}\sin \frac{(q_2+q_3)\pi }{2} +\alpha ^2{x^*}^2\left((\omega _0^*)^{q_2}\sin \frac{q_2\pi }{2}\right.\right.\\ &\quad\left.\left.+(\omega _0^*)^{q_3} \sin \frac{q_3\pi }{2}\right)+k_1\alpha x^*(\omega _0^*)^{q_3}\sin \frac{q_3\pi }{2}\right] +\left[(q_1+q_2+q_3)(\omega _0^*)^{q_1+q_2+q_3-1}\cos \frac{(q_1+q_2+q_3-1)\pi }{2}+ \alpha x^*(q_1+q_2)\right.\\ &\quad\times(\omega _0^*)^{q_1+q_2-1}\cos \frac{(q_1+q_2-1)\pi }{2} +\alpha x^*(q_1+q_3)(\omega _0^*)^{q_1+q_3-1} \cos \frac{(q_1+q_3-1)\pi }{2}+k_1(q_1+q_3)(\omega _0^*)^{q_1+q_3-1} \cos \frac{(q_1+q_3-1)\pi }{2}\\&\quad \left.+(\alpha ^2{x^*}^2 -\gamma ^2{(x^*)}^2+k_1\alpha x^*) ~q_1(\omega _0^*){q_1-1}\cos \frac{(q_1-1)\pi }{2} -\gamma ^2{(x^*)}^2q_2(\omega _0^*)^{q_2-1}\cos \frac{(q_2-1)\pi }{2}- \gamma ^2{(x^*)}^2q_3(\omega _0^*)^{q_3-1}\cos \frac{(q_3-1)\pi }{2}\right]\\ &\quad\times\sin \omega _0^*\tau _0^* +\left[(q_1+q_2+q_3)(\omega _0^*)^{q_1+q_2+q_3-1}\sin \frac{(q_1+q_2+q_3-1)\pi }{2} +\alpha x^*(q_1+q_2)s^{q_1+q_2-1}\sin \frac{(q_1+q_2-1)\pi }{2}+\alpha x^*(q_1+q_3)\right.\\&\quad\times (\omega _0^*)^{q_1+q_3-1}\sin \frac{(q_1+q_3-1)\pi }{2} +(\alpha ^2{(x^*)}^2-\gamma ^2{(x^*)}^2)~q_1(\omega _0^*)^{q_1-1} \sin \frac{(q_1-1)\pi }{2}-\gamma ^2{(x^*)}^2 q_2(\omega _0^*)^{q_2-1}\sin \frac{(q_2-1)\pi }{2}-\gamma ^2{(x^*)}^2q_3\\ &\quad\left.\times(\omega _0^*)^{q_3-1}\sin \frac{(q_3-1)\pi }{2}\right]\cos \omega _0^*\tau _0^*. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, L., Cao, J., Huang, C. et al. Bifurcation control in the delayed fractional competitive web-site model with incommensurate-order. Int. J. Mach. Learn. & Cyber. 10, 173–186 (2019). https://doi.org/10.1007/s13042-017-0707-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-017-0707-3

Keywords