Skip to main content

Advertisement

Springer Nature Link
Log in

Nonsmooth exponential synchronization of coupled neural networks with delays: new switching design

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

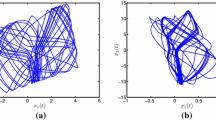
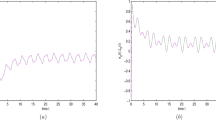
This paper considers the exponential synchronization for a class of coupled time-delayed neural networks with discontinuous activations. Based on differential inclusions theory, set-valued analysis, and by constructing suitable coupling function and Lyapunov function, designing a novel discontinuous controller, when the controller and activation functions are both discontinuous, the global exponential synchronization for the coupled neural networks can be achieved. Especially, we consider a new Lyapunov–Krasovskii functional which is time-dependent, and the results in this paper are applicable to the undirected weighted networks. Finally, to demonstrate the correctness of our results, a numerical example is provided to illustrate it. Our results extend previously known researches.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Wang D, Huang L (2014) Periodicity and global exponential stability of generalized Cohen-Grossberg neural networks with discontinuous activations and mixed delays. Neural Netw 51:80–95

    Article  MATH  Google Scholar 

  2. Akhmet M, Lmaz E (2012) Global exponential stability of neural networks with non-smooth and impact activations. Neural Netw 34:18–27

    Article  MATH  Google Scholar 

  3. Yang X, Cao J (2013) Exponential synchronization of delayed neural networks with discontinuous activations. IEEE Trans Circuits Syst I 60(9):2431–2439

    Article  MathSciNet  Google Scholar 

  4. Qin S, Xue X, Wang P (2013) Global exponential stability of almost periodic solution of delayed neural networks with discontinuous activations. Info Sci 220:367–378

    Article  MathSciNet  MATH  Google Scholar 

  5. Schiepek G, Tominschek I, Heinzel S et al (2013) Discontinuous patterns of brain activation in the psychotherapy process of obsessive-compulsive disorder: converging results from repeated FMRI and daily self-reports. Plos One 8(8):e71863

    Article  Google Scholar 

  6. Forti M, Nistri P (2003) Global convergence of neural networks with discontinuous neuron activations. IEEE Trans Circuits Syst I 50(11):1421–1435

    Article  MathSciNet  MATH  Google Scholar 

  7. Forti M, Nistri P, Papini D (2005) Global exponential stability and global convergence in finite time of delayed neural networks with infinite gain. IEEE Trans Neural Netw Learn Syst 16(6):1449–1463

    Article  Google Scholar 

  8. Forti M, Grazzini M, Nistri P et al (2006) Generalized Lyapunov approach for convergence of neural networks with discontinuous or non-Lipschitz activations. Phys D 214(1):88–99

    Article  MathSciNet  MATH  Google Scholar 

  9. Allegretto W, Papini D, Forti M (2010) Common asymptotic behavior of solutions and almost periodicity for discontinuous, delayed, and impulsive neural networks. IEEE Trans Neural Netw 21(7):1110–1125

    Article  Google Scholar 

  10. Duan L, Huang L, Cai Z (2014) Existence and stability of periodic solution for mixed time-varying delayed neural networks with discontinuous activations. Neurocomputing 123:255–265

    Article  Google Scholar 

  11. Cai Z, Huang L, Zhang L (2015) New exponential synchronization criteria for time-varying delayed neural networks with discontinuous activations. Neural Netw 65:105–114

    Article  MATH  Google Scholar 

  12. Liu X, Su H, Chen M (2016) A switching approach to designing finite-time synchronization controllers of coupled neural networks. IEEE Trans Neural Netw Learn Syst 27(2):471–482

    Article  MathSciNet  Google Scholar 

  13. Wang Y, Cao J (2013) Cluster synchronization in nonlinearly coupled delayed networks of non-identical dynamic systems. Nonlinear Anal 14(1):842–851

    Article  MathSciNet  MATH  Google Scholar 

  14. Shen J, Cao J (2011) Finite-time synchronization of coupled neural networks via discontinuous controllers. Cognit Neurodyn 5(4):373–385

    Article  Google Scholar 

  15. Tang Y, Wong W (2013) Distributed synchronization of coupled neural networks via randomly occurring control. IEEE Trans Neural Netw Learn Syst 24(3):435–447

    Article  Google Scholar 

  16. Volos C, Kyprianidis I, Stouboulos I et al (2015) Memristor: a new concept in synchronization of coupled neuromorphic circuits. J Eng Sci Technol Rev 8(2):157–173

    Article  Google Scholar 

  17. Wang Y, Xie L, De Souza C (1997) Robust control of a class of uncertain nonlinear systems. Syst Control Lett 19(2):139–149

    Article  MathSciNet  MATH  Google Scholar 

  18. Aubin J, Cellina A (1984) Differential inclusions. Springer, New York, pp 8–13

    Book  MATH  Google Scholar 

  19. LaSalle J (1976) The stability of dynamical systems. SIAM, Philadelphia

    Book  MATH  Google Scholar 

  20. Filippov A (1988) Differential equations with discontinuous right-hand sides and differential inclusions. Nonlinear Anal Nonlinear Diff Equ 154(2):265–288

    MATH  Google Scholar 

  21. Clarke F (1990) Optimization and nonsmooth analysis. SIAM, Philadelphia

    Book  MATH  Google Scholar 

  22. Karimi H, Gao H (2010) New delay-dependent exponential synchronization for uncertain neural networks with mixed time delays. IEEE Trans Syst Man Cybern 40(1):173–185

    Article  Google Scholar 

  23. Zhang H, Ma T, Huang G et al (2010) Robust global exponential synchronization of uncertain chaotic delayed neural networks via dual-stage impulsive control. IEEE Trans Syst Man Cybern 40(3):831–844

    Article  Google Scholar 

  24. Zhang H, Wang Z, Liu D (2014) A comprehensive review of stability analysis of continuous-time recurrent neural networks. IEEE Trans Neural Netw Learn Syst 25(7):1229–1262

    Article  Google Scholar 

  25. Zhang H, Liu Z, Huang G et al (2010) Novel weighting-delay-based stability criteria for recurrent neural networks with time-varying delay. IEEE Trans Neural Netw 21(1):91–106

    Article  Google Scholar 

  26. Liu Y, Wang Z, Liu X (2008) Exponential synchronization of complex networks with Markovian jump and mixed delays. Phys Lett A 372(22):3986–3998

    Article  MathSciNet  MATH  Google Scholar 

  27. Li L, Huang L (2009) Dynamical behaviors of a class of recurrent neural networks with discontinuous neuron activations. Appl Math Model 33(12):4326–4336

    Article  MathSciNet  MATH  Google Scholar 

  28. Zhang L, Huang L, Cai Z (2016) Finite-time stabilization control for discontinuous time-delayed networks: new switching design. Neural Netw 75:84–96

    Article  Google Scholar 

  29. Guo Z, Wang J, Yan Z (2015) Global exponential synchronization of two memristor-based recurrent neural networks with time delays via static or dynamic coupling. IEEE Trans Syst Man Cybern 45(2):235–249

    Article  Google Scholar 

  30. Cai Z, Huang L, Guo Z et al (2012) On the periodic dynamics of a class of time-varying delayed neural networks via differential inclusions. Neural Netw 33:97–113

    Article  MATH  Google Scholar 

  31. Zhang W, Li C, Huang T et al (2015) Synchronization of memristor-based coupling recurrent neural networks with time-varying delays and impulses. IEEE Trans Neural Netw Learn Syst 26(12):3308–3313

    Article  MathSciNet  Google Scholar 

  32. Yang X (2014) Can neural networks with arbitrary delays be finite-timely synchronized? Neurocomputing 143:275–281

    Article  Google Scholar 

  33. Yang X, Song Q, Liang J et al (2015) Finite-time synchronization of coupled discontinuous neural networks with mixed delays and nonidentical perturbations. J Frankl Inst 352(10):4382–4406

    Article  MathSciNet  MATH  Google Scholar 

  34. Tang Z, Park J, Jung H (2015) Exponential synchronization for coupled neural networks with time-varying delay under single impulsive controller. The 27th Chinese control and decision conference, (2015 CCDC). IEEE pp 1708–1713

  35. Liu X, Chen T (2007) Exponential synchronization of nonlinear coupled dynamical networks with a delayed coupling. Phys A 381:82–92

    Article  Google Scholar 

  36. Feng J, Yu F, Zhao Y (2016) Exponential synchronization of nonlinearly coupled complex networks with hybrid time-varying delays via impulsive control. Nonlinear Dyn 85:621–632

    Article  MathSciNet  MATH  Google Scholar 

  37. Zhou B, Liao X, Huang T et al (2015) Pinning exponential synchronization of complex networks via event-triggered communication with combinational measurements. Neurocomputing 157:199–207

    Article  Google Scholar 

  38. Yang X, Cao J, Ho D (2015) Exponential synchronization of discontinuous neural networks with time-varying mixed delays via state feedback and impulsive control. Cognit Neurodyn 9(2):113–128

    Article  Google Scholar 

  39. Rakkiyappan R, Dharani S, Zhu Q (2015) Stochastic sampled-data H\(_{\infty }\) synchronization of coupled neutral-type delay partial differential systems. J Frankl Inst 352(10):4480–4502

    Article  MathSciNet  MATH  Google Scholar 

  40. Rakkiyappan R, Dharani S, Zhu Q (2015) Synchronization of reaction-diffusion neural networks with time-varying delays via stochastic sampled-data controller. Nonlinear Dyn 79(1):485–500

    Article  MathSciNet  MATH  Google Scholar 

  41. Rakkiyappan R, Latha V, Zhu Q et al (2017) Exponential synchronization of Markovian jumping chaotic neural networks with sampled-data and saturating actuators. Nonlinear Anal Hybrid Syst 24:28–44

    Article  MathSciNet  MATH  Google Scholar 

  42. Zhu Q, Cao J (2012) \(p\)th moment exponential synchronization for stochastic delayed Cohen–Grossberg neural networks with Markovian switching. Nonlinear Dyn 67(1):829–845

    Article  MATH  Google Scholar 

  43. Zhu Q, Cao J (2011) Adaptive synchronization under almost every initial data for stochastic neural networks with time-varying delays and distributed delays. Commun Nonlinear Sci Numer Simul 16(4):2139–2159

    Article  MathSciNet  MATH  Google Scholar 

  44. Zhu Q, Cao J (2010) Adaptive synchronization of chaotic Cohen–Crossberg neural networks with mixed time delays. Nonlinear Dyn 61(3):517–534

    Article  MathSciNet  MATH  Google Scholar 

  45. Yang X, Zhu Q, Huang C (2011) Generalized lag-synchronization of chaotic mix-delayed systems with uncertain parameters and unknown perturbations. Nonlinear Anal Real World Appl 12(1):93–105

    Article  MathSciNet  MATH  Google Scholar 

  46. Zhou C, Zhang W, Yang X et al (2017) Finite-time synchronization of complex-valued neural networks with mixed delays and uncertain perturbations. Neural Process Lett 46(1):271–291

    Article  Google Scholar 

  47. Yang X, Feng Z, Feng J et al (2016) Synchronization of discrete-time neural networks with delays and Markov jump topologies based on tracker information. Neural Netw Off J Int Neural Netw Soc 85(C):157–164

    Google Scholar 

  48. Wang J, Feng J, Xu C et al (2015) Pinning synchronization of nonlinearly coupled complex networks with time-varying delays using M-matrix strategies. Neurocomputing 177(C):89–97

    Google Scholar 

  49. Zhang W, Tang Y, Wu X et al (2017) Synchronization of nonlinear dynamical networks with heterogeneous impulses. IEEE Trans Circ Syst I Regul Pap 61(4):1220–1228

    Article  Google Scholar 

  50. Wang J, Wu H, Huang T et al (2017) Pinning control for synchronization of coupled reaction-diffusion neural networks with directed topologies. IEEE Trans Syst Man Cybern Syst 46(8):1109–1120

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (11771059).

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Science, Changsha University, Changsha, 410022, People’s Republic of China

    Chao Yang

  2. School of Mathematical and Statistics, Changsha University of Science and Technology, Changsha, 410114, Hunan, People’s Republic of China

    Lihong Huang

Authors
  1. Chao Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Lihong Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Lihong Huang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, C., Huang, L. Nonsmooth exponential synchronization of coupled neural networks with delays: new switching design. Int. J. Mach. Learn. & Cyber. 10, 623–630 (2019). https://doi.org/10.1007/s13042-017-0742-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-017-0742-0

Keywords