Skip to main content

Advertisement

Springer Nature Link
Log in

Novel decision-making algorithms based on intuitionistic fuzzy rough environment

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

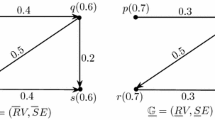
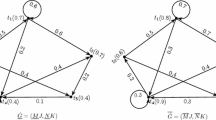
Abstract

Intuitionistic fuzzy sets and rough sets are two different mathematical models to deal the problem of how to understand and manipulate imperfect knowledge. An intuitionistic fuzzy rough framework is made by combining these two models, which is a more flexible and expressive for modeling and processing incomplete information in information systems. In this research study, we introduce intuitionistic fuzzy rough graphs, and describe certain types of intuitionistic fuzzy rough graphs with several examples. We present applications of intuitionistic fuzzy rough graphs in decision-making problems. We develop efficient algorithms to solve decision-making problems and compute time complexity of each algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353

    MATH  Google Scholar 

  2. Bhutani KR (1989) On automorphism of fuzzy graphs. Pattern Recognit Lett 9(3):159–162

    MathSciNet  MATH  Google Scholar 

  3. Atanassov KT (1986) Intuitionististic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    MathSciNet  Google Scholar 

  4. Atanassov KT (1999) Intuitionistic fuzzy sets: theory and applications. Springer Physica-Verlag, Berlin

    MATH  Google Scholar 

  5. Atanassov KT, Pasi G, Yager R, Atanassova V (2003) Intuitionistic fuzzy graph interpretations of multi-person multi-criteria decision making. Proceedings of the 3rd Conference of the European Society for Fuzzy Logic and Technology, Zittau, Germany, September 10–12, pp 115–119

  6. Atanassov KT, Pasi G, Yager R (2007) Intuitionistic fuzzy interpretations of multi-criteria multi-person and multi-measurement tool decision making. Int J Syst Sci 36(14):859–868

    MathSciNet  MATH  Google Scholar 

  7. Pawlak Z (1991) Rough sets-theoretical aspects to reasoning about data. Kluwer Academic Publisher, Boston

    MATH  Google Scholar 

  8. Pawalak Z (1982) Rough sets. Int J Comput Inf Sci 11(5):341–356

    Google Scholar 

  9. Liu GL (2010) Rough set theory based on two universal sets and its applications. Knowl Based Syst 23(2):110–115

    Google Scholar 

  10. Griffin G, Chen Z (1998) Rough set extension of Tcl for data mining. Knowl Based Syst 11(3–4):249–253

    Google Scholar 

  11. Pei DW, Xu ZB (2007) Transformation of rough set models. Knowl Based Syst 20(8):745–751

    Google Scholar 

  12. Dai JH, Hu H, Wu WZ, Qian YH, Huang DB (2017) Maximal discernibility pairs based approach to attribute reduction in fuzzy rough sets. IEEE Transactions on Fuzzy Systems. https://doi.org/10.1109/TFUZZ.2017.2768044

  13. Dai JH, Wei BJ, Zhang XH, Zhang QH (2017) Uncertainty measurement for incomplete interval-valued information systems based on a-weak similarity. Knowl Based Syst 136:159–171

    Google Scholar 

  14. Li J, Kumar Cherukuri Aswani, Mei Changlin, Wang Xizhao (2017) Comparison of reduction in formal decision contexts. Int J Approx Reason 80:100–122

    MathSciNet  MATH  Google Scholar 

  15. Li J, Mei C, Lv Y (2013) Incomplete decision contexts: approximate concept construction, rule acquisition and knowledge reduction. Int J Approx Reason 54(1):149–165

    MathSciNet  MATH  Google Scholar 

  16. Wang C, Shao M, He Q, Qian Y, Qi Y (2016) Feature subset selection based on fuzzy neighborhood rough sets. Knowl Based Syst 111(1):173–179

    Google Scholar 

  17. Wang C, Hu Q, Wang X, Chen D, Qian Y Feature selection based on neighborhood discrimination index. IEEE Transactions on Neural Networks and Learning Systems. https://doi.org/10.1109/TNNLS.2017.2710422

  18. Wang C, He Q, Shao M, Hu Q Feature selection based on maximal neighborhood discernibility. International journal of machine learning and cybernetics. https://doi.org/10.1007/s13042-017-0712-6

  19. Wang C, He Q, Shao M, Xua Y, Hu Q (2017) A unified information measure for general binary relations. Knowl Based Syst 135(1):18–28

    Google Scholar 

  20. Zhang XH (2017) Fuzzy anti-grouped filters and fuzzy normal filters in pseudo-BCI algebras. J Intell Fuzzy Syst 33:1767–1774

    MATH  Google Scholar 

  21. Zhang XH, Park C, Wu SP (2018) Soft set theoretical approach to pseudo-BCI algebras. J Intell Fuzzy Syst 34:559–568

    Google Scholar 

  22. Dubios D, Prade H (1990) Rough fuzzy and fuzzy rough sets. Int J Gen Syst 17(2–3):191–209

    MATH  Google Scholar 

  23. Chakrabarty K, Biswas R, Nanda S (2000) Fuzziness in rough sets. Fuzzy Sets Syst 110(2):247–251

    MathSciNet  MATH  Google Scholar 

  24. Mi JS, Zhang WX (2002) Composition of general fuzzy approximation spaces. Springer, Berlin, pp 497–501

    MATH  Google Scholar 

  25. Cornelis C, De Cock M, Kerre EE (2003) Intuitionistic fuzzy rough sets: at the crossroads of imperfect knowledge. Expert Syst 20(5):260–271

    Google Scholar 

  26. Xu W, Liu Y, Sun W Intuitionistic fuzzy rough sets model based on \((\Theta , \Phi )\)-operators. 2012 9th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2012): 234–238

  27. Zhou L, Wu WZ (2008) On generalerized intuitionistic fuzzy rough approximation operators. Inf Sci 178(11):2448–2465

    MATH  Google Scholar 

  28. Huang B, Guo C, Zhuang YL, Li H, Zhou X (2014) Intuitionistic fuzzy multigranulation rough sets. Inf Sci 277:299–320

    MathSciNet  MATH  Google Scholar 

  29. Wu WZ Intuitionistic fuzzy rough sets determined by intuitionistic fuzzy implicators. 2010 IEEE International Conference on Granular Computing, 536–540

  30. Guo ZL, Yang HL, Wang J (2015) Rough set over dual-universes in intuitionistic fuzzy approximation space and its application. J Intell Fuzzy Syst 28(1):169–178

    MathSciNet  MATH  Google Scholar 

  31. Yang HL, Li SG, Guo ZL, Ma CH (2012) Transformation of bipolar fuzzy rough set models. Knowl Based Syst 27:60–68

    Google Scholar 

  32. Yang HL, Li SG, Wang S, Wang J (2012) Bipolar fuzzy rough set model on two different universes and its application. Knowl Based Syst 35:94–101

    Google Scholar 

  33. Zhu K, Zhan J (2016) Fuzzy parameterized fuzzy soft sets and decision making. Int J Mach Learn Cybern 7(6):1207–1212

    Google Scholar 

  34. Zhan J, Liu Q, Herawan T (2017) A novel soft rough set: soft rough hemirings and its multicriteria group decision making. Appl Soft Comput 54:393–402

    Google Scholar 

  35. Shahzamanian MH, Shirmohammadi M, Davvaz B (2010) Roughness in Cayley graphs. Inf Sci 180:3362–3372

    MathSciNet  MATH  Google Scholar 

  36. Kauffman A (1973) Introduction a la Theorie des Sous-emsembles Flous. Masson et Cie 12(4):213–227

    Google Scholar 

  37. Rosenfeld A (1975) Fuzzy graphs. In: Zadeh LA, Fu KS, Shimura M (eds) Fuzzy sets and their applications. Academic Press, New York

    Google Scholar 

  38. Bhattacharya P (1987) Some remarks on fuzzy graphs. Pattern Recognit Lett 6(5):297–302

    MATH  Google Scholar 

  39. Mordeson JN, Peng CS (1994) Operations on fuzzy graphs. Inf Sci 79(3–4):159–170

    MathSciNet  MATH  Google Scholar 

  40. Mordeson JN, Nair PS (2000) Fuzzy graphs and fuzzy hypergraphs. Springer Physica-Verlag, Heidelberg Gmbl

    MATH  Google Scholar 

  41. Sunitha MS, Vijayakumar A (2002) Complement of a fuzzy graph. Indian J Pure Appl Math 33(9):1451–1464

    MathSciNet  MATH  Google Scholar 

  42. Mathew S, Sunitha M (2009) Types of arcs in a fuzzy graph. Inf Sci 179(11):1760–1768

    MathSciNet  MATH  Google Scholar 

  43. Mathew S, Sunitha M (2013) Strongest strong cycles and fuzzy graphs. IEEE Trans Fuzzy Syst 21:1096–1104

    Google Scholar 

  44. Pramanik T, Samanta S, Pal M (2016) Interval-valued fuzzy planar graphs. Int J Mach Learn Cybern 7:653664. https://doi.org/10.1007/s13042-014-0284-7

    Google Scholar 

  45. NagoorGani A, Akram M, Vijayalakshmi P (2016) Certain types of fuzzy sets in a fuzzy graph. Int J Mach Learn Cybern 7:573579. https://doi.org/10.1007/s13042-014-0267-8

    Google Scholar 

  46. Myithili KK, Parvathi R, Akram M (2016) Certain types of intuitionistic fuzzy directed hypergraphs. Int J Mach Learn Cybern 7:287295. https://doi.org/10.1007/s13042-014-0253-1

    Google Scholar 

  47. Borzooei RA, Rashmanlou H (2017) New concepts of vague graphs. Int J Mach Learn Cybern 8:10811092. https://doi.org/10.1007/s13042-015-0475-x

    Google Scholar 

  48. Parvathi R, Karunambigai MG, Atanassov KT (2009) Operations on intuitionistic fuzzy graphs. IEEE International Conference on Fuzzy Systems, Jeju Island, Korea 20–24:1396–1401

  49. Akram M, Ashraf A, Sarwar M (2014) Novel applications of intuitionistic fuzzy digraphs in decision support systems. The Scientific World Journal 2014. Article ID 904606

  50. Akram M, Saira N (2016) Fuzzy soft graphs with applications. J Intell Fuzzy Syst 30(6):3619–3632

    MATH  Google Scholar 

  51. Akram M, Shahzadi S (2016) Novel intuitionistic fuzzy soft multiple-attribute decision-making methods. Neural Computing and Applications. https://doi.org/10.1007/s00521-016-2543-x

  52. Akram M, Alshehri N, Davvaz B, Ashraf A (2016) Bipolar fuzzy digraphs in decision support systems. J. Multiple-Valued Logic Soft Comput 27:531–551

    MATH  Google Scholar 

  53. Molina-Solana M, Birch D, Guo Y (2017) Improving data exploration in graphs with fuzzy logic and large-scale visualisation. Appl Soft Comput 53:227–235

    Google Scholar 

  54. Akram M, Zafar F (2018) Journal of Applied Mathematics and Computing. https://doi.org/10.1007/s12190-018-1171-2

  55. Zafar F, Akram M (2018) A novel decision-making method based on rough fuzzy information. Int J Fuzzy Syst 20(3):1000–1014. https://doi.org/10.1007/s40815-017-0368-0

    MathSciNet  Google Scholar 

  56. Malik HM, Akram M (2018) A new approach based on intuitionistic fuzzy rough graphs for decision-making. J Intell Fuzzy Syst 34(4):2325–2342. https://doi.org/10.3233/JIFS-171395

    Google Scholar 

  57. Akram M, Malik HM, Shahzadi S, Smarandache F (2018) Neutrosophic soft rough graphs with application. Axioms 7(1): https://doi.org/10.3390/axioms7010014

Download references

Acknowledgements

The authors are very thankful to the Editor and referees for their valuable comments and suggestions for improving the paper. This research is partially supported by a grant of National Natural Science Foundation of China (11461025).

Author information

Authors and Affiliations

  1. Department of Mathematics, Hubei University for Nationalities, Enshi, 445000, People’s Republic of China

    Jianming Zhan

  2. Department of Mathematics, University of the Punjab, New Campus, Lahore, Pakistan

    Hafsa Masood Malik & Muhammad Akram

Authors
  1. Jianming Zhan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hafsa Masood Malik
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Muhammad Akram
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Muhammad Akram.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhan, J., Masood Malik, H. & Akram, M. Novel decision-making algorithms based on intuitionistic fuzzy rough environment. Int. J. Mach. Learn. & Cyber. 10, 1459–1485 (2019). https://doi.org/10.1007/s13042-018-0827-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-018-0827-4

Keywords