Abstract
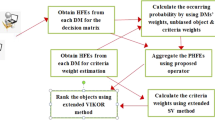
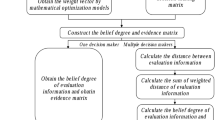
In this paper, multi-criteria decision-making (MCDM) methods with probabilistic hesitant fuzzy information are proposed based on the dominance degree of probabilistic hesitant fuzzy elements (PHFEs) and best worst method (BWM). First, we discuss the probabilistic distribution function of PHFE and the dominance degree matrix between two PHFEs. The dominance degree matrix is constructed based on the probabilistic distribution function of PHFE, which can be characterized as a fuzzy complementary judgment matrix. Second, BWM is extended to fuzzy preference relations based on the constructed dominance degree matrix. Subsequently, an algorithm is designed for selecting the best and worst weight vectors, and then two models are developed based on additive consistency and multiplicative consistency of fuzzy preference relations to derive the criteria weights. In addition, an algorithm is presented to improve the consistency of the dominance degree matrix when a desired consistency level is not achieved. Finally, the selection of best investment company is provided as an example to demonstrate the feasibility and effectiveness of the proposed methods.


Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Ivanco M, Hou G, Michaeli J (2017) Sensitivity analysis method to address user disparities in the analytic hierarchy process. Expert Syst Appl 90:111–126
Ahn BS (2017) The analytic hierarchy process with interval preference statements. Omega 67:177–185
Ren PJ, Xu ZS, Liao HC (2016) Intuitionistic multiplicative analytic hierarchy process in group decision making. Comput Ind Eng 101:513–524
Zhü KY (2014) Fuzzy analytic hierarchy process: fallacy of the popular methods. Eur J Oper Res 236:209–217
Kahraman C, Öztayşi B, Uçal Sarı İ, Turanoğlu E (2014) Fuzzy analytic hierarchy process with interval type-2 fuzzy sets. Knowl Based Syst 59:48–57
Liao HC, Xu ZS (2015) Consistency of the fused intuitionistic fuzzy preference relation in group intuitionistic fuzzy analytic hierarchy process. Appl Soft Comput 35:812–826
Otay İ, Oztaysi B, Onar SC, Kahraman C (2017) Multi-expert performance evaluation of healthcare institutions using an integrated intuitionistic fuzzy AHP&DEA methodology. Knowl Based Syst 133:90–106
Cao YX, Zhou H, Wang JQ (2018) An approach to interval-valued intuitionistic stochastic multi-criteria decision-making using set pair analysis. Int J Mach Learn Cybernet 9:629–640
Zhu B, Xu ZS (2014) Analytic hierarchy process-hesitant group decision making. Eur J Oper Res 239:794–801
Zhu B, Xu ZS, Zhang R, Hong M (2016) Hesitant analytic hierarchy process. Eur J Oper Res 250:602–614
Zhou W, Xu ZS, Asymmetric hesitant fuzzy sigmoid preference relations in the analytic hierarchy process. Inf Sci 358–359:191–207 (2016)
Santos LFdOM, Osiro L, Lima RHP (2017) A model based on 2-tuple fuzzy linguistic representation and analytic hierarchy process for supplier segmentation using qualitative and quantitative criteria. Expert Syst Appl 79:53–64
Franco CA (2014) On the analytic hierarchy process and decision support based on fuzzy-linguistic preference structures. Knowl Based Syst 70:203–211
Peng HG, Wang JQ, Cheng PF (2018) A linguistic intuitionistic multi-criteria decision-making method based on the Frank Heronian mean operator and its application in evaluating coal mine safety. Int J Mach Learn Cybernet 9:1053–1068
Abdullah L, Najib L (2014) A new type-2 fuzzy set of linguistic variables for the fuzzy analytic hierarchy process. Expert Syst Appl 41:3297–3305
He YQ, Du SP (2016) Classification of urban emergency based on fuzzy analytic hierarchy process. Proced Eng 137:630–638
Mangla SK, Govindan K, Luthra S (2017) Prioritizing the barriers to achieve sustainable consumption and production trends in supply chains using fuzzy analytical hierarchy process. J Clean Prod 151:509–525
Kuo CFJ, Lin CH, Hsu MW, Li MH (2017) Evaluation of intelligent green building policies in Taiwan—using fuzzy analytic hierarchical process and fuzzy transformation matrix. Energy Build 139:146–159
Zhou W, Xu ZS, Chen MH (2015) Preference relations based on hesitant-intuitionistic fuzzy information and their application in group decision making. Comput Ind Eng 87:163–175
García-Lapresta JL, Pérez-Román D (2016) Consensus-based clustering under hesitant qualitative assessments. Fuzzy Sets Syst 292:261–273
Wang JQ, Peng JJ, Zhang HY, Chen XH (2017) Outranking approach for multi-criteria decision-making problems with hesitant interval-valued fuzzy sets. Soft Comput. https://doi.org/10.1007/s13042-13016-10589-13049
Wang J, Wang JQ, Tian ZP, Zhao DY (2018) A multi-hesitant fuzzy linguistic multicriteria decision-making approach for logistics outsourcing with incomplete weight information. Int Trans Oper Res 25:831–856
Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25:529–539
Zhu B (2014) Decision method for research and application based on preference relation. Southeast University, Nanjing
Yu SM, Wang J, Wang JQ, Li L (2018) A multi-criteria decision-making model for hotel selection with linguistic distribution assessments. Appl Soft Comput 67:739–753
Zhou H, Wang JQ, Zhang HY (2017) Stochastic multicriteria decision-making approach based on SMAA-ELECTRE with extended gray numbers. Int Trans Oper Res. https://doi.org/10.1111/itor.12380
Xu ZS, Zhou W (2017) Consensus building with a group of decision makers under the hesitant probabilistic fuzzy environment. Fuzzy Optim Decis Mak 16:481–503
Peng HG, Zhang HY, Wang JQ (2018) Probability multi-valued neutrosophic sets and its application in multi-criteria group decision-making problems. Neural Comput Appl 30:363–383
Zhang S, Xu ZS, He Y (2017) Operations and integrations of probabilistic hesitant fuzzy information in decision making. Inf Fusion 38:1–11
Wang JQ, Cao YX, Zhang HY (2017) Multi-criteria decision-making method based on distance measure and choquet integral for linguistic Z-numbers. Cognit Comput 9:827–842
Zhou W, Xu ZS (2017) Expected hesitant VaR for tail decision making under probabilistic hesitant fuzzy environment. Appl Soft Comput 60:297–311
Li J, Wang JQ (2017) An extended QUALIFLEX method under probability hesitant fuzzy environment for selecting green suppliers. Int J Fuzzy Syst 19:1866–1879
Li J, Wang JQ (2017) Multi-criteria outranking methods with hesitant probabilistic fuzzy sets. Cognit Comput 9:611–625
Ding J, Xu ZS, Zhao N (2017) An interactive approach to probabilistic hesitant fuzzy multi-attribute group decision making with incomplete weight information. J Intell Fuzzy Syst 32:2523–2536
Wu ZB, Jin BM, Xu JP (2018) Local feedback strategy for consensus building with probability-hesitant fuzzy preference relations. Appl Soft Comput 67:691–705
Zhou W, Xu ZS (2017) Group consistency and group decision making under uncertain probabilistic hesitant fuzzy preference environment. Inf Sci 414:276–288
Wu ZB, Xu JP (2018) A consensus model for large-scale group decision making with hesitant fuzzy information and changeable clusters. Inf Fusion 41:217–231
Zhou W, Xu ZS (2018) Probability calculation and element optimization of probabilistic hesitant fuzzy preference relations based on expected consistency. IEEE Trans Fuzzy Syst 26:1367–1378
Zhang YX, Xu ZS, Wang H, Liao HC (2016) Consistency-based risk assessment with probabilistic linguistic preference relation. Appl Soft Comput 49:817–833
Zhang YX, Xu ZS, Liao HC (2018) A consensus process for group decision making with probabilistic linguistic preference relations. Inf Sci 414:260–275
Rezaei J (2015) Best-worst multi-criteria decision-making method. Omega 53:49–57
Rezaei J (2016) Best-worst multi-criteria decision-making method: some properties and a linear model. Omega 64:126–130
Mou Q, Xu ZS, Liao HC (2017) A graph based group decision making approach with intuitionistic fuzzy preference relations. Comput Ind Eng 110:138–150
Mou Q, Xu ZS, Liao HC (2016) An intuitionistic fuzzy multiplicative best-worst method for multi-criteria group decision making. Inf Sci 374:224–239
Guo S, Zhao H (2017) Fuzzy best-worst multi-criteria decision-making method and its applications. Knowl Based Syst 121:23–31
Gupta H, Barua MK (2016) Identifying enablers of technological innovation for Indian MSMEs using best–worst multi criteria decision making method. Technol Forecast Soc Chang 107:69–79
Ren JZ, Liang HW, Chan FTS (2017) Urban sewage sludge, sustainability, and transition for Eco-City: multi-criteria sustainability assessment of technologies based on best-worst method. Technol Forecast Soc Chang 116:29–39
Rezaei J, Nispeling T, Sarkis J, Tavasszy L (2016) A supplier selection life cycle approach integrating traditional and environmental criteria using the best worst method. J Clean Prod 135:577–588
Rezaei J, Wang J, Tavasszy L (2015) Linking supplier development to supplier segmentation using best worst method. Expert Syst Appl 42:9152–9164
Liu BD (2005) A course in uncertainty theory. Tsinghua University Press, Beijing
Liu Y, Fan ZP, Zhang Y (2011) A method for stochastic multiple criteria decision making based on dominance degrees. Inf Sci 181:4139–4153
Xia MM, Xu ZS (2011) Hesitant fuzzy information aggregation in decision making. Int J Approx Reason 52:395–407
Kay E (1977) Graph theory with applications. J Oper Res Soc 28:237–238
Tanino T (1984) Fuzzy preference orderings in group decision making. Fuzzy Sets Syst 12:117–131
Wu ZB, Xu JP (2012) A concise consensus support model for group decision making with reciprocal preference relations based on deviation measures. Fuzzy Sets Syst 206:58–73
Xu ZS, Hu H (2010) Projection models for intuitionistic fuzzy multiple attribute decision making. Int J Inf Technol Decis Mak 9:267–280
Wei GW, Zhao XF, Lin R (2013) Some hesitant interval-valued fuzzy aggregation operators and their applications to multiple attribute decision making. Knowl Based Syst 46:43–53
Acknowledgements
The authors thank the editors and anonymous reviewers for their helpful comments and suggestions. This work was supported by the National Natural Science Foundation of China (No. 71571193) and the Fundamental Research Funds for the Central Universities of Central South University (Nos. 2018zzts095).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Li, J., Wang, Jq. & Hu, Jh. Multi-criteria decision-making method based on dominance degree and BWM with probabilistic hesitant fuzzy information. Int. J. Mach. Learn. & Cyber. 10, 1671–1685 (2019). https://doi.org/10.1007/s13042-018-0845-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-018-0845-2