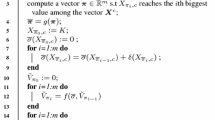Skip to main content
SpringerLink
Log in

Learning from correlation with extreme learning machine

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

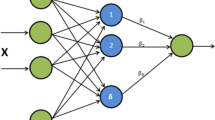
A seemingly unrelated regression (SUR) refers to several individual equations among which there is not an explicit connection such as one equation’s observation is another equation’s response, but there exists an implicit relation represented by correlated disturbances of response variables. In this paper, SUR is applied to extreme learning machine (ELM) which is a single hidden layer feed-forward neural network where input weights and hidden layer biases are randomly assigned but the weight parameters between hidden and output layers are least-square solutions of a regression equation. A correlation-based extreme learning machine is built using the auxiliary sample which is related to the main sample which we focus on. Considering the weights between hidden and output layers in ELM as a random vector, we derive an explicit representation for the vector’s covariance matrix. The proof of theorems and simulation process indicate that the stronger correlation between main sample and auxiliary sample is, the higher generalization ability is.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Zellner A (1962) An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias. J Am Stat Assoc 57(298):348–368

    Article  MathSciNet  MATH  Google Scholar 

  2. Hubert M, Verdonck T, Yorulmaz z (2016) Fast robust sur with economical and actuarial applications. Stat Anal Data Min ASA Data Sci J 10(2):77–88

    Article  MathSciNet  Google Scholar 

  3. Wang H (2010) Sparse seemingly unrelated regression modelling: applications in finance and econometrics. Comput Stat Data Anal 54(11):2866–2877

    Article  MathSciNet  MATH  Google Scholar 

  4. Foschi P, Kontoghiorghes EJ (2004) A computationally efficient method for solving sur models with orthogonal regressors. Linear Algebra Appl 388(1):193–200

    Article  MathSciNet  MATH  Google Scholar 

  5. Fraser D, Rekkas M, Wong A (2005) Highly accurate likelihood analysis for the seemingly unrelated regression problem. J Econom 127(1):17–33

    Article  MathSciNet  MATH  Google Scholar 

  6. Dufour J-M, Khalaf L (2002) Exact tests for contemporaneous correlation of disturbances in seemingly unrelated regressions. J Econom 106(1):143–170

    Article  MathSciNet  MATH  Google Scholar 

  7. Zellner A, Ando T (2010) A direct monte carlo approach for bayesian analysis of the seemingly unrelated regression model. J Econom 159(1):33–45

    Article  MathSciNet  MATH  Google Scholar 

  8. Zellner A, Huang DS (1962) Further properties of efficient estimators for seemingly unrelated regression equations. Int Econ Rev 3(3):300–313

    Article  MATH  Google Scholar 

  9. Magnus JR (1978) Maximum likelihood estimation of the gls model with unknown parameters in the disturbance covariance matrix. J Econom 7(3):281–312

    Article  MathSciNet  MATH  Google Scholar 

  10. Kakwani NC (1967) The unbiasedness of Zellner’s seemingly unrelated regression equations estimators. Publ Am Stat Assoc 62(317):141–142

    Article  MathSciNet  MATH  Google Scholar 

  11. Zellner A (1963) Estimators for seemingly unrelated regression equations: some exact finite sample results. J Am Stat Assoc 58(304):977–992

    Article  MATH  Google Scholar 

  12. Revankar NS (1974) Some finite sample results in the context of two seemingly unrelated regression equations. J Am Stat Assoc 69(345):187–190

    Article  MathSciNet  MATH  Google Scholar 

  13. Revankar NS (1976) Use of restricted residuals in sur systems: some finite sample results. J Am Stat Assoc 71(353):183–188

    Article  MathSciNet  MATH  Google Scholar 

  14. Liu A (2002) Efficient estimation of two seemingly unrelated regression equations. J Multivar Anal 82(2):445–456

    Article  MathSciNet  MATH  Google Scholar 

  15. Ma T, Ye R (2010) Efficient improved estimation of the parameters in two seemingly unrelated regression models. J Stat Plan Inference 140(9):2749–2754

    Article  MathSciNet  MATH  Google Scholar 

  16. Wang L, Lian H, Singh RS (2011) On efficient estimators of two seemingly unrelated regressions. Stat Probab Lett 81(5):563–570

    Article  MathSciNet  MATH  Google Scholar 

  17. Zhao L, Xu X (2017) Generalized canonical correlation variables improved estimation in high dimensional seemingly unrelated regression models. Stat Probab Lett 126:119–126

    Article  MathSciNet  MATH  Google Scholar 

  18. Kurata H, Kariya T (1996) Least upper bound for the covariance matrix of a generalized least squares estimator in regression with applications to a seemingly unrelated regression model and a heteroscedastic model. Ann Stat 24(4):1547–1559

    Article  MathSciNet  MATH  Google Scholar 

  19. Chauvin Y, Rumelhart DE (1995) Back-propagation: theory, architecture, and applications. Lawrence Erlbaum Associates Inc., Hillsdale

    Google Scholar 

  20. Huang G-B, Zhu Q-Y, Siew CK (2006) Extreme learning machine: theory and applications. Neurocomputing 70(1–3):489–501

    Article  Google Scholar 

  21. Huang G-B, Zhou HM, Ding XJ, Zhang R (2012) Extreme learning machine for regression and multi-class classification. IEEE Trans Syst Man Cybern Part B Cybern 42(2):513–529

    Article  Google Scholar 

  22. Huang Z, Yu Y, Gu J (2015) A novel method for traffic sign recognition based on extreme learning machine. In: Intelligent control and automation, pp 1451–1456

  23. Zhang L, Wang X, Huang GB, Liu T, Tan X (2018) Taste recognition in e-tongue using local discriminant preservation projection. IEEE Trans Cybern PP(99):1–14

    Google Scholar 

  24. Wang J, Zhang L, Cao J-J, Han D (2018) Nbwelm: naive bayesian based weighted extreme learning machine. Int J Mach Learn Cybern 9(1):21–35

    Article  Google Scholar 

  25. Wang R, Chen D, Kwong S (2014) Fuzzy rough set based active learning. IEEE Trans Fuzzy Syst 22(6):1699–1704

    Article  Google Scholar 

  26. Wang R, Wang X-Z, Kwong S, Chen X (2017) Incorporating diversity and informativeness in multiple-instance active learning. IEEE Trans Fuzzy Syst 25(6):1460–1475

    Article  Google Scholar 

  27. Srivastava DG (1987) Seemingly unrelated regression models. Dekker, New York

    MATH  Google Scholar 

  28. Wang X-Z, Wang R, Chen X (2018) Discovering the relationship between generalization and uncertainty by incorporating complexity of classification. IEEE Trans Cybern 48(2):703–715

    Article  Google Scholar 

  29. Cao J, Zhang K, Luo M, Yin C, Lai X (2016) Extreme learning machine and adaptive sparse representation for image classification. Neural Netw 81(C):91–102

    Article  Google Scholar 

  30. Zhao H, Guo X, Wang M, Li T, Pang C, Georgakopoulos D (2018) Analyze EEG signals with extreme learning machine based on PMIS feature selection. Int J Mach Learn Cybern 9(2):243–249

    Article  Google Scholar 

  31. Wang R, Chow C-Y, Kwong S (2016) Ambiguity based multiclass active learning. IEEE Trans Fuzzy Syst 24(1):242–248

    Article  Google Scholar 

  32. Luo X, Yang X, Jiang C, Ban X (2018) Timeliness online regularized extreme learning machine. Int J Mach Learn Cybern 9(3):465–476

    Article  Google Scholar 

  33. Zhao X, Cao W, Zhu H, Ming Z, Ashfaq RAR (2018) An initial study on the rank of input matrix for extreme learning machine. Int J Mach Learn Cybern 9(5):867–879

    Article  Google Scholar 

  34. Zhao L, Yan L, Xu X (2018) High correlated residuals improved estimation in the high dimensional SUR model. Commun Stat Simul Comput 47(7):1583–1605. https://doi.org/10.1080/03610918.2017.1309429

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We would like to express our gratitude to all those who helped me during the writing of this paper. We gratefully acknowledge the help of our supervisor, Prof. XiZhao Wang, who has offered us valuable suggestions to revise and improve this paper. This work was supported in part by the National Natural Science Foundation of China (Grant 61772344, Grant 61732011, and Grant 61811530324), in part by the Natural Science Foundation of SZU (Grant 827-000140, Grant 827-000230, and Grant 2017060), in part by Basic Research Project of Knowledge Innovation Program in ShenZhen (JCYJ20180305125850156).

Author information

Authors and Affiliations

  1. The College of Computer Science and Software Engineering, Shenzhen University, Shenzhen, 518060, China

    Li Zhao

  2. Guangdong Key Laboratory of Intelligent Information Processing, Shenzhen University, Shenzhen, 518060, China

    Li Zhao

  3. Department of Information Management, The National Police University for Criminal Justice, Beijing, China

    Jie Zhu

Authors
  1. Li Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jie Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li Zhao.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

A Proof of Theorem 3

A Proof of Theorem 3

Proof

For the sake of brevity we Let

$$\begin{aligned} \mathbf{I}-\mathbf{H}{^*}(\mathbf{H}{^*}'\mathbf{H}^*)^{-1}\mathbf{H}{^*}'= \mathbf{A}_1,\,\, \mathbf{I}-\mathbf{H}(\mathbf{H}'\mathbf{H})^{-1}\mathbf{H}'= \mathbf{A}_2 \end{aligned}$$

Then

$$\begin{aligned} \frac{{\hat{\sigma}}_{12}}{{\hat{\sigma}}_{22}}=\frac{(\mathbf{T}^*-\mathbf{H}^*\hat{\varvec{\beta}}_{ ols}^*)'(\mathbf{T} -\mathbf{H} \hat{\varvec{\beta}}_{ ols})}{(\mathbf{T} -\mathbf{H} \hat{\varvec{\beta}}_{ ols})'(\mathbf{T} -\mathbf{H} \hat{\varvec{\beta}}_{ ols})}=\frac{\mathbf{T}{^*}'\mathbf{A}_1\mathbf{A}_2\mathbf{T}}{\mathbf{T}'\mathbf{A}_2\mathbf{T}} \end{aligned}$$

and

$$\begin{aligned}&var(\hat{\varvec{\beta}}^*_F) =var(\hat{\varvec{\beta}}_{ ols}^*) +(\mathbf{H}{^*}'\mathbf{H}{^*})^{-1}\mathbf{H}{^*}' var\left( \frac{\mathbf{T}{^*}'\mathbf{A}_1\mathbf{A}_2\mathbf{T}}{\mathbf{T}'\mathbf{A}_2\mathbf{T}}\mathbf{A}_2\mathbf{T}\right) \mathbf{H}{^*} (\mathbf{H}{^*}'\mathbf{H}{^*})^{-1}\\&\quad -2(\mathbf{H}{^*}'\mathbf{H}^*)^{-1}\mathbf{H}{^*}'Cov\left( \mathbf{T}^*,\frac{\mathbf{T}{^*}'\mathbf{A}_1\mathbf{A}_2\mathbf{T}}{\mathbf{T}'\mathbf{A}_2\mathbf{T}}\mathbf{A}_2\mathbf{T}\right) \mathbf{H}{^*}(\mathbf{H}{^*}'\mathbf{H}^*)^{-1}. \end{aligned}$$

From Theorem 1 we know that \(var(\hat{\varvec{\beta}}_{ ols}^*) =\sigma _{11}(\mathbf{H}{^*}'\mathbf{H}^*)^{-1}\).

Obviously \(\mathbf{A}_i\) and \(\mathbf{I}-\mathbf{A}_i\) are both symmetric idempotent matrices with order M and orthogonal to each other, \(i=1,2\). Let \(k_1=rank(\mathbf{H}{^*})\), and \(k_2=rank(\mathbf{H})\). There exists and \(M\times (M-k_i)\) full column rank matrix \(\mathbf{B}_i\) such that \(\mathbf{A}_i=\mathbf{B}_i\mathbf{B}_i'\), \(i=1,2\) and \(M\times (M-k_1)\) matrix \(\mathbf{P}\) such that \(\mathbf{I}-\mathbf{A}_1=\mathbf{P}\mathbf{P}'\). We know that \(\mathbf{P}'\mathbf{P}=\mathbf{I}_{k_1}, \mathbf{P}'\mathbf{B}_1=\mathbf{O}_{(k_1)\times (M-k_1)}\) and \(\mathbf{B}_i'\mathbf{B}_i=\mathbf{I}_{M-k_i},\)\(i=1,2\). Let

$$\begin{aligned} \varvec{\gamma}=\frac{1}{\sqrt{\sigma _{11}}}\mathbf{T}^*\,\, \varvec{\eta}=\frac{1}{\sqrt{\sigma _{22}}}\mathbf{T}\,\, \varvec{\kappa}=\frac{1}{\sqrt{\sigma _{11}}}(\mathbf{P}' \mathbf{T}^*-\mathbf{H}{^*} \varvec{\beta _1}). \end{aligned}$$
(12)

Then

$$\begin{aligned} \left[ \begin{array}{c} \varvec{\kappa}\\ \varvec{\gamma}\\ \varvec{\eta} \end{array}\right] \thicksim N\left( \left( \begin{array}{c} \mathbf{0}\\ \mathbf{0}\\ \mathbf{0} \end{array} \right) ,\ \left[ \begin{array}{ccc} I_{k_1}&{}\quad \mathbf{O}&{}\quad \rho _{21}\mathbf{P}'\mathbf{B}_2\\ \mathbf{O}&{}\quad I_{M-k_1}&{}\quad \rho _{12}\mathbf{B}_1'\mathbf{B}_2\\ \rho _{21}\mathbf{B}_2'\mathbf{P}&{}\quad \rho _{21}\mathbf{B}_2'\mathbf{B}_1&{}\quad I_{M-k_2} \end{array}\right] \right) . \end{aligned}$$
(13)

and

$$\begin{aligned} \begin{aligned} var(\hat{\varvec{\beta}}^*_F)&=\sigma _{11}\left( \mathbf{H}{^*}'\mathbf{H}{^*}\right) ^{-1}+\sigma _{11}\left( \mathbf{H}{^*}'\mathbf{H}{^*}\right) ^{-1}\mathbf{H}{^*}'\left( var\left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) \right. \\&\quad -\left. 2\sqrt{\sigma _{11}} cov\left( \left( \sqrt{\sigma _{11}}\mathbf{P}\varvec{\kappa}+\mathbf{H}{^*}\beta _1\right) ,\frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) \right) \mathbf{H}{^*}\left( \mathbf{H}{^*}'\mathbf{H}{^*}\right) ^{-1}. \end{aligned} \end{aligned}$$
(14)

According to (13) we have that

$$\begin{aligned} \varvec{\gamma}|\varvec{\eta}\thicksim M\left( \rho _{12}\mathbf{B}_1'\mathbf{B}_2\varvec{\eta},\ \ \ I_{M-k_1}-\rho _{12}^2\mathbf{B}_1'\mathbf{B}_2\mathbf{B}_2'\mathbf{B}_1\right) , \end{aligned}$$
(15)

and

$$\begin{aligned} E\left( \varvec{\kappa} | (\varvec{\gamma}', \varvec{\eta}')' \right) =-\frac{\rho _{12}^2}{1-\rho _{12}^2}\mathbf{P}'\mathbf{A}_2\mathbf{B}_1\varvec{\gamma}+\rho _{12}\mathbf{P}'\mathbf{B}_2\varvec{\eta}+\frac{\rho _{12}^3}{1-\rho _{12}^2}\mathbf{P}'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}. \end{aligned}$$
(16)

From (15) we know that

$$\begin{aligned} \begin{aligned} E\left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) = E\left( E\left( \left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) |\varvec{\eta} \right) \right) = \rho _{12}E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{B}_1\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) . \end{aligned} \end{aligned}$$

Since the distribution of \(\varvec{\eta}\) is is symmetric about the origin, we have that

$$\begin{aligned} E\left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) =\mathbf{O}. \end{aligned}$$
(17)

From (17) we know that

$$\begin{aligned} \begin{aligned} var\left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right)&= E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{B}_1\varvec{\gamma}\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\right) \\ {}&= E\left( E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{B}_1\varvec{\gamma}\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\right) |\varvec{\eta}\right) \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} E(\varvec{\gamma}\varvec{\gamma}'|\varvec{\eta})=E(\varvec{\gamma}|\varvec{\eta})E(\varvec{\gamma}'|\varvec{\eta})+var(\varvec{\gamma}|\varvec{\eta}). \end{aligned}$$
(18)

Combining with (15) we know that

$$\begin{aligned} \begin{aligned}&var\left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) \\ {}&\quad = E\left( \varvec{\eta}'\mathbf{B}_2'\mathbf{B}_1\frac{(\rho _{12}^2\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\mathbf{B}_1+I_{M-k_1}-\rho _{12}^2\mathbf{B}_1'\mathbf{B}_2\mathbf{B}_2'\mathbf{B}_1)}{\varvec{\eta}'\varvec{\eta}\varvec{\eta}'\varvec{\eta}} \mathbf{B}_1'\mathbf{B}_2\varvec{\eta}\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\right) \\&\quad = \rho _{12}^2 E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'}{\varvec{\eta}'\varvec{\eta}\varvec{\eta}'\varvec{\eta}}\right) \\&\qquad + (1-\rho _{12}^2)E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'}{\varvec{\eta}'\varvec{\eta}\varvec{\eta}'\varvec{\eta}}\right) . \end{aligned} \end{aligned}$$
(19)

It is easy to check that \(\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\) and \(\mathbf{I}_{M-k_2}-\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\) are both symmetric idempotent matrice. Since \(\text {rank}(\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2)=tr(\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2)=tr(\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2)=tr(\mathbf{A}_2\mathbf{A}_1)=M-k_1-k_2,\) we can find an \((M-k_2)\times (M-k_1-k_2)\)-matrix \(\mathbf{Q}_2^c\) and an \((M-k_2)\times k_1\)-matrix \(\mathbf{Q}_2\) such that \(\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2=\mathbf{Q}_2^c \mathbf{Q}_2^{c'}\), \(I_{M-k_2}-\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2=\mathbf{Q}_2\mathbf{Q}_2'\) and \((\mathbf{Q}_2,\mathbf{Q}_2^{c})\) is an orthogonal matrix.

Let

$$\begin{aligned} \left( \begin{array}{c} \varvec{\zeta}\\ \varvec{\zeta}^c \end{array} \right) =\left( \begin{array}{c} \mathbf{Q}_2'\varvec{\eta} \\ \mathbf{Q}_2^{c'}\varvec{\eta} \end{array} \right) =\left( \begin{array}{c} \mathbf{Q}_2' \\ \mathbf{Q}_2^{c'} \end{array} \right) \varvec{\eta} \end{aligned}$$

Then

$$\begin{aligned} \varvec{\eta}=\mathbf{Q}_2\varvec{\zeta}+\mathbf{Q}_2^{c}\varvec{\zeta}^c\,\, \text {and}\,\, \varvec{\eta}'\varvec{\eta}=(\mathbf{Q}_2\varvec{\zeta}+\mathbf{Q}_2^{c}\varvec{\zeta}^c)'(\mathbf{Q}_2\varvec{\zeta}+\mathbf{Q}_2^{c}\varvec{\zeta}^c)=\varvec{\zeta}'\varvec{\zeta}+\varvec{\zeta}^{c'}\varvec{\zeta}^c, \end{aligned}$$

Furthermore,

$$\begin{aligned} \begin{aligned}&E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'}{\varvec{\eta}'\varvec{\eta}\varvec{\eta}'\varvec{\eta}}\right) \\&\quad = \mathbf{B}_2E\left( \frac{(\varvec{\eta}'\mathbf{Q}_2^c \mathbf{Q}_2^{c'}\varvec{\eta})^2}{(\varvec{\eta}'\varvec{\eta})^2}(\mathbf{Q}_2\mathbf{Q}_2')\varvec{\eta}\varvec{\eta}'\right) (\mathbf{Q}_2\mathbf{Q}_2')\mathbf{B}_2'\\&\quad = \mathbf{B}_2E\left( \frac{(\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}{(\varvec{\zeta}' \varvec{\zeta}+\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}\mathbf{Q}_2\varvec{\zeta}\varvec{\zeta}'\mathbf{Q}_2'\right) \mathbf{B}_2'\\&\quad = \mathbf{B}_2\mathbf{Q}_2E\left( \frac{(\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}{(\varvec{\zeta}' \varvec{\zeta}+\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}\varvec{\zeta}\varvec{\zeta}'\right) \mathbf{Q}_2'\mathbf{B}_2'\\ \end{aligned} \end{aligned}$$

Let

$$\begin{aligned} E\left( \frac{(\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}{(\varvec{\zeta}' \varvec{\zeta}+\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}\varvec{\zeta}\varvec{\zeta}'\right) =\Delta \end{aligned}$$

and write \(\varvec{\zeta}=(w_1,w_2,\ldots ,w_{k_1})^T\). Then the (i, j)th element of \(\Delta\) is denoted by \(\Delta (i,j)\) where \(\Delta (i,j)=E\Bigg [\frac{(\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}{(\varvec{\zeta}' \varvec{\zeta}+\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}w_iw_j\Bigg ], (1\le i,j \le k_1)\). Since \(w_1,w_2,\ldots ,w_{k_1}\) are independent and identically distributed random variables, when \(i\ne j,\)

$$\begin{aligned} \Delta (i,j)=E\left( \frac{(\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2w_iw_j}{\left( \sum \nolimits _{l=1}^{k_1} w_l^2+\varvec{\zeta}^{c'} \varvec{\zeta}^c\right) ^2}\right) =0. \end{aligned}$$

When \(i=j<k_1\)

$$\begin{aligned} \begin{aligned}&E\left( \frac{(\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2w_i^2}{\left( \sum \nolimits _{l=1}^{k_1} w_l^2+\varvec{\zeta}^{c'} \varvec{\zeta}^c\right) ^2}\right) \\&\quad =E\left( \frac{\left( \varvec{\zeta}^{c'} \varvec{\zeta}^c\right) ^2\frac{1}{k_1}\sum \nolimits _{l=1}^{k_1}w_l^2}{\left( \sum \nolimits _{l=1}^{k_1} w_l^2+\varvec{\zeta}^{c'} \varvec{\zeta}^c\right) ^2}\right) \\&\quad =\frac{1}{k_1}E\left( \frac{\left( \varvec{\zeta}^{c'} \varvec{\zeta}^c\right) ^2}{\left( \sum \nolimits _{l=1}^{k_1} w_l^2+\varvec{\zeta}^{c'} \varvec{\zeta}^c\right) ^2}\left( \sum \nolimits _{l=1}^{k_1}w_l^2+\varvec{\zeta}^{c'} \varvec{\zeta}^c-\varvec{\zeta}^{c'} \varvec{\zeta}^c\right) \right) \\&\quad =\frac{1}{k_1}E\left( \left( \frac{\varvec{\zeta}^{c'} \varvec{\zeta}^c}{\varvec{\zeta}'\varvec{\zeta}+\varvec{\zeta}^{c'} \varvec{\zeta}^c}\right) ^2(\varvec{\zeta}'\varvec{\zeta}+\varvec{\zeta}^{c'} \varvec{\zeta}^c) - \left( \frac{\varvec{\zeta}^{c'} \varvec{\zeta}^c}{\varvec{\zeta}'\varvec{\zeta}+\varvec{\zeta}^{c'} \varvec{\zeta}^c}\right) ^3(\varvec{\zeta}'\varvec{\zeta}+\varvec{\zeta}^{c'} \varvec{\zeta}^c)\right) \end{aligned} \end{aligned}$$

Since \(\varvec{\zeta}^{c^T} \varvec{\zeta}^c\sim \chi ^2(M-k_2-k_1),\,\,\varvec{\zeta}^T\varvec{\zeta}\sim \chi ^2(k_1)\) and \(\varvec{\zeta}^{c^T} \varvec{\zeta}^c\) is independent of \(\varvec{\zeta}^T\varvec{\zeta}\). we have that

$$\begin{aligned}&\varvec{\zeta}^T\varvec{\zeta}+\varvec{\zeta}^{c^T} \varvec{\zeta}^c\sim \chi ^2(M-k_2) ,\,\text {and}\\&\quad \frac{\varvec{\zeta}^{c^T} \varvec{\zeta}^c}{\varvec{\zeta}^T\varvec{\zeta}+\varvec{\zeta}^{c^T} \varvec{\zeta}^c}\sim \beta \left( \frac{M-k_2-k_1}{2},\,\,\frac{k_1}{2}\right) \end{aligned}$$

meanwhile \(\varvec{\zeta}^{c^T} \varvec{\zeta}^c/(\varvec{\zeta}^T\varvec{\zeta}+\varvec{\zeta}^{c^T}\varvec{\zeta}^c)\) is independent of \(\varvec{\zeta}^T\varvec{\zeta}+\varvec{\zeta}^{c^T} \varvec{\zeta}^c\). Hence

$$\begin{aligned} \begin{aligned} E\left( \frac{(\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2\frac{1}{k_1}\sum \nolimits _{l=1}^{k_1}w_l^2}{(\sum \nolimits _{l=1}^{k_1} w_l^2+\varvec{\zeta}^{c'} \varvec{\zeta}^c)^2}\right) =\frac{(M-k_2-k_1)(M-k_2-k_1+2)}{(M-k_2+2)(M-k_2+4)}. \end{aligned} \end{aligned}$$

Combining with \(\mathbf{A}_1\mathbf{A}_2=\mathbf{A}_2\mathbf{A}_1\) and \(\mathbf{A}_2\mathbf{P}=\mathbf{P}\), we have that

$$\begin{aligned} \begin{aligned}&E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'}{\varvec{\eta}'\varvec{\eta}\varvec{\eta}'\varvec{\eta}}\right) \\&\quad = \frac{(M-k_2-k_1)(M-k_2-k_1+2)}{(M-k_2+2)(M-k_2+4)} \mathbf{B}_2(I_{M-k_2}-\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2)\mathbf{B}_2'\\&\quad =\frac{(M-k_2-k_1)(M-k_2-k_1+2)}{(M-k_2+2)(M-k_2+4)}\mathbf{P} , \end{aligned} \end{aligned}$$
(20)

Similarly

$$\begin{aligned} \begin{aligned} E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'}{\varvec{\eta}'\varvec{\eta}\varvec{\eta}'\varvec{\eta}}\right) =\frac{(M-k_2-k_1)}{(M-k_2)(M-k_2+2)}\mathbf{P} \end{aligned} \end{aligned}$$
(21)

Substituting (20) and (21) into (19) , we have that

$$\begin{aligned} \begin{aligned}&var\left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) =\frac{M-k_2-k_1}{M-k_2+2}\\&\quad \times \,\left( \frac{ (M-k_2-k_1+2)\rho _{12}^2}{ M-k_2+4} +\frac{1-\rho _{12}^2}{M-k_2}\right) \mathbf{P} \end{aligned} \end{aligned}$$
(22)

Then we calculate the last term in (14). From (15) and the symmetry of distribution we have that

$$\begin{aligned}&E\left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'\right) =E\left( E\left( \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'|\varvec{\eta}\right) \right) \\&\quad =\rho _{12}E\left( \frac{\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'\right) =0. \end{aligned}$$

Combining with (17) and (16) we know that

$$\begin{aligned} \begin{aligned}&cov\left( \left( \sqrt{\sigma _{11}}\mathbf{P}\varvec{\kappa}+\mathbf{H}{^*} \varvec{\beta _1}\right) ,\frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) \\&\quad = E\left( \mathbf{H}{^*}'\left( \sqrt{\sigma _{11}}\mathbf{P}\varvec{\kappa}+\mathbf{H}{^*} \varvec{\beta _1}\right) \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'\right) \\&\quad =\sqrt{\sigma _{11}} \mathbf{P}E\left( E\left( \left( \varvec{\kappa}\frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'\right) |\left( \varvec{\gamma},\varvec{\eta}\right) \right) \right) \\&\quad =\sqrt{\sigma _{11}} \mathbf{P}E\left( \left( -\frac{\rho _{12}^2}{1-\rho _{12}^2}\mathbf{P}'\mathbf{A}_2\mathbf{B}_1\varvec{\gamma}\right. \right. \\&\qquad \left. \left. +\rho _{12}\mathbf{P}'\mathbf{B}_2\varvec{\eta}+\frac{\rho _{12}^3}{1-\rho _{12}^2}\mathbf{P}'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}\right) \frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'\right) \\&\quad = \sqrt{\sigma _{11}} (\mathbf{I}-\mathbf{A}_1) \left( -\frac{\rho _{12}^2}{1-\rho _{12}^2}\mathbf{B}_1E\left( E\left( \frac{\varvec{\gamma}\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'|\varvec{\eta}\right) \right) \right. \\&\qquad \left. +\rho _{12} \mathbf{B}_2E\left( E\left( \frac{\varvec{\eta}\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'|\varvec{\eta}\right) \right) \right) \\&\quad =-\sqrt{\sigma _{11}} (\mathbf{I}-\mathbf{A}_1) \frac{\rho _{12}^2}{1-\rho _{12}^2}\mathbf{B}_1 E\left( \frac{(\rho _{12}^2\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\mathbf{B}_1+I_{M-k_1}-\rho _{12}^2\mathbf{B}_1'\mathbf{B}_2\mathbf{B}_2'\mathbf{B}_1)}{\varvec{\eta}'\varvec{\eta}}\right. \\&\qquad \mathbf{B}_1'\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\Bigg ) +\sqrt{\sigma _{11}}\rho _{12}^2 M_1E \left( \frac{\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'A_1\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'\right) . \end{aligned} \end{aligned}$$

Here, the third equation is hold for \(\mathbf{P}\mathbf{P}'=\mathbf{I}-\mathbf{A}_1,\, (\mathbf{I}-\mathbf{A}_1)\mathbf{A}_2=(\mathbf{I}-\mathbf{A}_1),\) and \((\mathbf{I}-\mathbf{A}_1)\mathbf{A}_1=\mathbf{0}.\) The last equation is hold for (15) and (18). Note that \((\mathbf{I}-\mathbf{A}_1) \mathbf{B}_1\mathbf{B}_1'=(\mathbf{I}-\mathbf{A}_1) \mathbf{A}_1=\mathbf{0},\) therefore

$$\begin{aligned} \begin{aligned}&cov\left( \left( \sqrt{\sigma _{11}}\mathbf{P}\varvec{\kappa}+\mathbf{H}{^*} \varvec{\beta}_1\right) ,\frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) \\&\quad =\sqrt{\sigma _{11}} \rho _{12}^2 M_1E\left( \frac{\mathbf{B}_2\varvec{\eta}\varvec{\eta}'\mathbf{B}_2'\mathbf{A}_1\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\varvec{\eta}'\mathbf{B}_2'\right) . \end{aligned} \end{aligned}$$

Follows the same method as in Eq. (20), we get that

$$\begin{aligned} \begin{aligned}&cov\left( \left( \sqrt{\sigma _{11}}\mathbf{P}\varvec{\kappa}+\mathbf{H}{^*} \varvec{\beta}_1\right) ,\frac{\varvec{\gamma}'\mathbf{B}_1'\mathbf{B}_2\varvec{\eta}}{\varvec{\eta}'\varvec{\eta}}\mathbf{B}_2\varvec{\eta}\right) \\&\quad =\sqrt{\sigma _{11}} \rho _{12}^2\frac{M-k_2-k_1}{M-k_2+2} (\mathbf{I}-\mathbf{B}_1). \end{aligned} \end{aligned}$$
(23)

Substituting (22), (23) and into (14), we finally have the variance of \({\hat{\beta}}_{1FG}\) is

$$\begin{aligned} Cov(\hat{\varvec{\beta}}^*_F)&=\sigma _{11} (\mathbf{H}{^*}'\mathbf{H}{^*})^{-1}\left( 1+\frac{(M-k_2-k_1)}{(M-k_2)(M-k_2+2)}\right. \\&\quad \Bigg ( \rho _{12}^2 \left. \left. \left( \frac{-M^2+2Mk_2-Mk_1-7M k_2^2+k_1k_2+7k_2-4}{M-k_2+4}\right) +1 \right) \right) \end{aligned}$$

Let

$$\begin{aligned} a=\frac{(M-k_2-k_1)}{(M-k_2)(M-k_2+2)}, \end{aligned}$$

and

$$\begin{aligned} b= & {} \left( \frac{-M^2+2Mk_2-Mk_1-7M k_2^2+k_1k_2+7k_2-4}{M-k_2+4}\right) \\= & {} \left( M+3+k_1-k_2-\frac{8+4k_1}{M-k_2+4}\right) . \end{aligned}$$

Then

$$\begin{aligned} Cov(\hat{\varvec{\beta}}^*_F)=\sigma _{11}(\mathbf{H}{^*}'\mathbf{H}{^*})^{-1}\left( 1+a\left( 1-b \rho ^2 \right) \right) . \end{aligned}$$

\(\square\)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, L., Zhu, J. Learning from correlation with extreme learning machine. Int. J. Mach. Learn. & Cyber. 10, 3635–3645 (2019). https://doi.org/10.1007/s13042-019-00949-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-019-00949-y

Keywords

Search

Navigation