Implement an uncertain vector approach to solve entropy-based four-dimensional transportation problems with discounted costs

Abstract

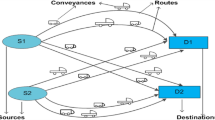
In this research paper, using uncertainty theory we introduced and developed entropy-based uncertain four-dimensional transportation problem with fixed charges, discounted costs, and vehicle costs. In this transportation system, we considered a discount policy on the transportation cost which depends on the basis of the transported amount. Here, the discounted costs are in the form of all unit discounts (AlUD), incremental quantity discounts (InQD), and the combination of these two. The main objective is to minimize the total transportation cost via maximum entropy which ensures the number of items to be transported from some source to some destinations by some conveyances through some routes. For optimizing the proposed model, using uncertain programming techniques, we have developed two different models such as expected value programming model and expected constrained programming model. Then, Using minimizing distance method and linear weighted method we formulated and solved the equivalent deterministic transformation of these two constructed models. Finally, to show the application of the proposed models and methods we presented a numerical example with optimal results.

Appendices

Appendix

Preliminaries

In this section, we will discuss uncertain variables, uncertain vector, and uncertain entropy function.

1.1 Uncertain variables and uncertain vectors

In this section, we briefly discuss some fundamental definitions, theorems, and examples of uncertain variables and uncertain vectors.

Definition A.1

[31] We assume that $(\Gamma ,{\mathcal {L}})$ be a measurable space, where ${\mathcal {L}}$ be a $\sigma$ -algebra on a nonempty set $\Gamma$. A set function ${\mathcal {M}}:{\mathcal {L}}\rightarrow [0, 1]$ is called an uncertain measure if it satisfies the following four axioms:

1. Normality axiom : ${\mathcal {M}}\{ \Gamma \}$=1 for the universal set $\Gamma$.

2. Duality axiom: ${\mathcal {M}}\{\Lambda \}$+${\mathcal {M}}\{\Lambda ^{C}\}$=1, for any event $\Lambda \in {\mathcal {L}}$ and $\Lambda ^{C}$ is a complement of $\Lambda$.

3. Subadditivity axiom : For every countable sequence of events $\Lambda _{1},\Lambda _{2},...$, we have

$$\begin{aligned} {\mathcal {M}}{\bigg \{}\bigcup _{n=1}^{\infty }\Lambda _{n} \bigg \}\le \sum _{n=1}^{\infty }{\mathcal {M}}\bigg \{\Lambda _{n} \bigg \} \end{aligned}$$

4. Product axiom : Let $(\Gamma _n,{\mathcal {L}}_n,{\mathcal {M}}_n)$ be uncertainty spaces for $n=1,2,\cdots$.Then, the product uncertain measure ${\mathcal {M}}$ is an uncertain measure satisfying the following condition:

$$\begin{aligned} {\mathcal {M}}{\bigg \{}\prod _{n=1}^{\infty }\Lambda _{n} \bigg \} = \bigwedge _{n=1}^{\infty }{\mathcal {M}}_n\bigg \{\Lambda _{n} \bigg \} \end{aligned}$$

where $\Lambda _{n}$ are arbitrarily chosen events from ${\mathcal {L}}_{n}$ for $n=1,2,\cdots$. respectively.

In this case, the triplet $(\Gamma ,{\mathcal {L}},{\mathcal {M}})$ is called an uncertainty space (US) where $\Gamma$ be a non-empty set, ${\mathcal {L}}$ be a $\sigma$ -algebra on the nonempty set $\Gamma$ and ${\mathcal {M}}$ be the uncertain measure (UM).

Definition A.2

[31] An uncertain variable (UV) is denoted by $\zeta$ and which is a function from an US $(\Gamma ,{\mathcal {L}}, {\mathcal {M}})$ to the set of real numbers such that

$$\begin{aligned} \{\zeta \ \in B\}=\{\gamma \in \Gamma |{\zeta }(\gamma )\in B\} \end{aligned}$$

is an event for any Borel set B of real numbers.

For any Borel sets $B_1,B_2,\cdots B_n$ of real numbers, the UVs ${\zeta _1},{\zeta _2} ,\cdots ,{\zeta _n}$ are said to be independent if

$$\begin{aligned} {\mathcal {M}}{\bigg \{}\bigcap ^n_{i=1} (\zeta _i\ \in B_i)\bigg \}= \bigwedge _{i=1}^{n}{\mathcal {M}}\{\zeta _i\ \in B_i \} \end{aligned}$$

Definition A.3

[31] The uncertainty distribution (UD) $\Phi (x)$ of an UV $\zeta$ is defined by

$$\begin{aligned} \Phi (x)= {\mathcal {M}} \{{\zeta } \le x \} \qquad \forall ~~ x\in \mathfrak {R}. \end{aligned}$$

Definition A.4

[32] An UD $\Phi (x)$ is said to be regular UD if it is a strictly increasing and continuous function with respect to x at which $0< \Phi (x) < 1$, and

$$\begin{aligned} \lim _{x\rightarrow -\infty } \Phi (x)= 0 \qquad \qquad \text {and} \qquad \qquad \lim _{x\rightarrow \infty } \Phi (x)= 1 \end{aligned}$$

Definition A.5

[32] Let ${\zeta }$ be an UV with a regular UD $\Phi (x)$. Then the inverse function $\Phi ^{-1}(\beta )$ is called the inverse UD of ${\zeta }$, where $\beta \in [0,1]$.

Example A.1

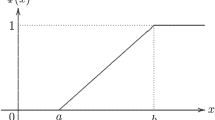
[31] An UV ${\zeta }$ is said to be zigzag UV if ${\zeta }$ follows a zigzag UD as given below :

$$\begin{aligned} \Phi (x)= \left\{ \begin{array}{lll} 0 &{} \text{ if } &{} x\le a \\ \frac{x-a}{2(b-a)} &{} \text{ if } &{}a< x\le b \\ \frac{x+c-2b}{2(c-b)} &{} \text{ if } &{}b< x\le c \\ 1 \text{ if } x> c \\ \end{array} \right. \end{aligned}$$

where ${\zeta }$ is denoted by ${\zeta } \sim {\mathcal {Z}}(a,b,c)$ such that $a<b<c$ and a, b, c are any real numbers.

The UD of a zigzag UV ${\mathcal {Z}}(a,b,c)$ is displayed in figure 5.

Fig. 5

Zigzag UD

Example A.2

[31] The inverse UD of zigzag UV ${\mathcal {Z}}(a,b,c)$ is defined as

$$\begin{aligned} \Phi ^{-1}(\beta )= \left\{ \begin{array}{lll} (1-2\beta ) a +2\beta b &{} \text{ if } &{} \beta < 0.5 \\ (2-2\beta ) b +(2\beta -1) c &{} \text{ if } &{} \beta \ge 0.5 \\ \end{array} \right. \end{aligned}$$

Example A.3

[33] Let ${\zeta } \sim {\mathcal {Z}}(a,b,c)$ be a zigzag UV. Then its inverse UD $\Phi ^{-1}(\beta )=\frac{1}{2}[(1-\beta )a+ b+ \beta c]$ and the expected value of ${\zeta }$ can be expressed as

$$\begin{aligned} E[{\zeta }]= \int _{0}^{1} \frac{1}{2}[(1-\beta )a+ b+ \beta c] d\beta \end{aligned}$$

Theorem A.1

[34] Let ${\zeta _{1}},{\zeta _{2}},{\zeta _{3}} ,\cdots ,{\zeta _{n}}$ be independent UVs with regular UDs $\Phi _1,\Phi _2,\Phi _3,\cdots ,\Phi _n$ respectively. If $f(\zeta _{1},{\zeta _{2}},{\zeta _{3}} ,\cdots ,{\zeta _{n}})$ is strictly increasing w. r. to ${\zeta _1},{\zeta _2},{\zeta _3} ,\cdots ,{\zeta _m}$ and strictly decreasing w. r. to ${\zeta _{m+1}},{\zeta _{m+2}}, {\zeta _{m+3}},\cdots ,{\zeta _{n}}$, then

$$\begin{aligned} {\zeta }=f({\zeta _1},{\zeta _2},{\zeta _3} ,\cdots ,{\zeta _n}) \end{aligned}$$

has an inverse UD

$$\begin{aligned} \Psi ^{-1}(\beta )= & {} f\bigg ( \Phi _1^{-1}(\beta ),\Phi _2^{-1}(\beta ),\cdots ,\\&\Phi _m^{-1}(\beta ),\Phi _{m+1}^{-1}(1-\beta ),\cdots ,\Phi _n^{-1}(1-\beta )\bigg ). \end{aligned}$$

and has an expected value

$$\begin{aligned} E[\zeta ]= & {} \int _{0}^{1} f\bigg ( \Phi _1^{-1}(\beta ),\Phi _2^{-1}(\beta ),\cdots ,\\&\Phi _m^{-1}(\beta ),\Phi _{m+1}^{-1}(1-\beta ),\cdots ,\Phi _n^{-1}(1-\beta )\bigg ) d\beta . \end{aligned}$$

Definition A.6

[31] The expected value of of an UV ${\zeta }$ is denoted by $E[{\zeta }]$ and defined as

$$\begin{aligned} E[{\zeta }]= \int _{0}^{+\infty }{\mathcal {M}} \{{\zeta } \ge r\} dr- \int _{-\infty }^{0}{\mathcal {M}} \{{\zeta } \le r\} dr \end{aligned}$$

if at least one of the two integrals is finite.

Theorem A.2

[34] Let ${\zeta }$ be an UV with regular UD $\Phi (x)$. If the expected value exists, then

$$\begin{aligned} E[{\zeta }]=\int _{0}^{1}\Phi ^{-1}(\beta ) d\beta \end{aligned}$$

where $\Phi ^{-1}(\beta )$ is the inverse UD of UV ${\zeta }$ such that $\beta \in [0,1]$ is the predetermined confidence level.

Theorem A.3

[31] Let us assume that ${\zeta _{1}}$ and ${\zeta _{2}}$ be two independent UVs with finite expected values. Then for any real numbers $a_{1}$ and $a_{2}$, we have

$$\begin{aligned} E[a_{1}\,{\zeta _{1}}+a_{2}\,{\zeta _{2}}]= a_{1}\,E[{\zeta _{1}}] +a_{2}\,E[{\zeta _{2}}]. \end{aligned}$$

Theorem A.4

[31] A function $\Phi ^{-1}(\beta )$ is an inverse UD of an UV ${\zeta }$ if and only if

$$\begin{aligned} {\mathcal {M}}\bigg \{{\zeta }\le \Phi ^{-1}(\beta ) \bigg \}\ = \beta \qquad \forall ~~ \beta \in [0,1]. \end{aligned}$$

Theorem A.5

[32] Let us assume that $y(x,\zeta _{1},{\zeta _{2}},{\zeta _{3}} ,\cdots ,{\zeta _{n}})$ is a constraint function also this is strictly increasing w. r. to ${\zeta _1},{\zeta _2},{\zeta _3} ,\cdots ,{\zeta _m}$ and strictly decreasing w. r. to ${\zeta _{m+1}},{\zeta _{m+2}}, {\zeta _{m+3}},\cdots ,{\zeta _{n}}$ are also independent UVs with UDs $\Phi _1,\Phi _2,\Phi _3,\cdots ,\Phi _n$ respectively, then the chance constraint

$$\begin{aligned} {\mathcal {M}}\bigg \{y(x,\zeta _{1},{\zeta _{2}},{\zeta _{3}} ,\cdots ,{\zeta _{n}})\le 0 \bigg \}\ \ge \beta \qquad \forall ~~ \beta \in [0,1] \end{aligned}$$

fulfills if and only if

$$\begin{aligned}&y\bigg ( x, \Phi _1^{-1}(\beta ),\Phi _2^{-1}(\beta ),\cdots ,\Phi _m^{-1}(\beta ),\\&\quad \Phi _{m+1}^{-1}(1-\beta ),\cdots ,\Phi _n^{-1}(1-\beta )\bigg )\le 0. \end{aligned}$$

Definition A.7

[31] A n-dimensional uncertain vector (UnV) is a function $\nu$ from an US $(\Gamma ,{\mathcal {L}},{\mathcal {M}})$ to the set of n-dimensional real vectors V such that $\{\nu \ \in B\}$ is an event for any n-dimensional Borel set B.It can be write in symbolically,

$$\begin{aligned} \nu :(\Gamma ,{\mathcal {L}},{\mathcal {M}}) \rightarrow V \end{aligned}$$

Hence, we can write, $(\nu _1, \nu _2, \cdots ,\nu _n)$ is an UnV if and only if $\nu _1, \nu _2, \cdots ,\nu _n$ are UVs.

The joint UD of an UnV $(\nu _1, \nu _2, \cdots ,\nu _n)$ is defined as

$$\begin{aligned}&\Phi (r_1, r_2, r_3, \cdots , r_n ) \\&\quad = {\mathcal {M}}\big \{ \nu _1 \le r_1, \nu _2 \le r_2, \nu _3 \le r_3, \cdots ,\nu _n\le r_n \big \}\ \end{aligned}$$

for any real values $r_1, r_2, r_3, \cdots , r_n$.

Theorem A.6

[31] Let $\nu _1, \nu _2, \nu _3, \cdots ,\nu _n$ be independent UVs with UDs $\Phi _{1},\Phi _{2},\Phi _{3},\cdots , \Phi _{n}$, respectively. Then, the UnV $(\nu _1, \nu _2, \nu _3, \cdots ,\nu _n)$ has a joint UD

$$\begin{aligned}&\Phi (r_1, r_2, r_3, \cdots , r_n ) \\&\quad = \Phi _{1}(r_1)\wedge \Phi _{2}(r_2)\wedge \Phi _{3}(r_3)\wedge \cdots \wedge \Phi _{n}(r_n). \end{aligned}$$

for any real values $r_1, r_2, r_3, \cdots , r_n$.

Proof

Since $\nu _1, \nu _2, \nu _3, \cdots ,\nu _n$ be independent UVs, we have

$$\begin{aligned} \Phi (r_1, r_2, r_3, \cdots , r_n )= & {} {\mathcal {M}}{\bigg \{}\bigcap ^n_{k=1} (\nu _k\ \le r_{k} )\bigg \}\\= & {} \bigwedge _{k=1}^{n}{\mathcal {M}}\{\nu _k \le r_{k} \} = \bigwedge _{k=1}^{n} \Phi _{k} (r_{k}). \end{aligned}$$

for any real values $r_1, r_2, r_3, \cdots , r_n$. Hence the theorem is proved.

Definition A.8

[32] For any n-dimensional Borel sets $B_1,B_2,\cdots B_n$ of real vectors, the n-dimensional UnVs ${\nu _1},{\nu _2} ,\cdots ,{\nu _n}$ are said to be independent if any one of the following conditions is fulfilled:

$$\begin{aligned}&(i) \,\, {\mathcal {M}}{\bigg \{}\bigcap ^n_{k=1} (\nu _k\ \in B_k)\bigg \}= \bigwedge _{k=1}^{n}{\mathcal {M}}\{\nu _k\ \in B_k \} \\&\quad (ii) \,\, {\mathcal {M}}{\bigg \{}\bigcup _{k=1}^{n} (\nu _k\ \in B_k)\bigg \}= \bigvee _{k=1}^{n}{\mathcal {M}}\{\nu _k\ \in B_k \} \end{aligned}$$

1.2 Concepts about entropy of uncertain variables

In this section, we will discuss the entropy of an UV with the UD. In 2009, Liu [32], a well-known mathematician, first given the idea of uncertain entropy theory.

Definition A.9

[32] Let us assume that ${\zeta }$ be an UV with UD $\Phi (x)$. Then its entropy is denoted by $H[\zeta ]$ and defined as:

$$\begin{aligned} H[\zeta ]=\int _{-\infty }^{\infty } S(\Phi (x)) \, \text {dx} = \int _{-\infty }^{\infty } S ({\mathcal {M}} \{{\zeta } \le x \}) \, \text {dx} \end{aligned}$$

where $S(t)= -t\,\text {ln}\, t -(1-t)\,\,\text {ln} (1-t)$.

Fig. 6

Graphical representation of entropy function

The geometric representation of entropy function $H[\zeta ]$ is displayed in figure 6. This figure follows that, the function S(t) is strictly concave shape on the interval [0, 1] and symmetric shape about $t=0.5$.

Theorem A.7

[34] If $\zeta \in [a, b]$ then $0\le H[\zeta ] \le \text {ln}\, 2$ and $H[\zeta ] = (b-a) \, \text {ln}\, 2$, with the corresponding UD is given below:

$$\begin{aligned} \Phi (x)= \left\{ \begin{array}{lll} 0 &{} \text{ if } &{}x< a \\ 0.5 &{} \text{ if } &{} a \le x\le b \\ 1 &{} \text{ if } &{} x \ge b. \\ \end{array} \right. \end{aligned}$$

where ${\zeta }$ is the UV and $H[\zeta ]$ is the entropy of ${\zeta }$ such that $a<b<c$ and a, b, c are any real numbers.

Theorem A.8

[34] Let ${\zeta }$ be an UV with regular UD $\Phi (x)$. If the entropy $H[\zeta ]$ exists, then

$$\begin{aligned} H[\zeta ]=\int _{0}^{1} \Phi ^{-1}(\beta ) \,\, \text {ln}\, \, \frac{\beta }{1-\beta } \,\, \text {d} \beta . \end{aligned}$$

Example A.6

[34] The inverse UD of zigzag UV ${\zeta } \sim {\mathcal {Z}}(a,b,c)$ is given by

$$\begin{aligned} \Phi ^{-1}(\beta )= \left\{ \begin{array}{lll} (1-2\beta ) a +2\beta b &{} \text{ if } &{} \beta < 0.5 \\ (2-2\beta ) b +(2\beta -1) c &{} \text{ if } &{} \beta \ge 0.5 \\ \end{array} \right. \end{aligned}$$

Then using theorem A.7 we get the entropy of ${\zeta }$:

$$\begin{aligned} H[\zeta ]=\int _{0}^{1} \Phi ^{-1}(\beta ) \,\, \text {ln}\, \, \frac{\beta }{1-\beta } \,\, \text {d} \beta = \frac{c-a}{2}. \end{aligned}$$

Theorem A.9

[6] Let us assume that ${\zeta _{1}},{\zeta _{2}},{\zeta _{3}} ,\cdots ,{\zeta _{n}}$ be independent UVs with regular UDs $\Phi _1,\Phi _2,\cdots ,\Phi _n$ respectively and if $f:\mathfrak {R}^{n} \rightarrow \mathfrak {R}$ is a strictly monotone function then the UV ${\zeta }=g\,({\zeta _1},{\zeta _2},{\zeta _3} ,\cdots ,{\zeta _n})$ has an entropy

$$\begin{aligned} H[\zeta ]= & {} \int _{0}^{1} g\,( \Phi _1^{-1}(\beta ),\Phi _2^{-1}(\beta ),\cdots ,\\&\Phi _n^{-1}(\beta )) \,\, \text {ln}\, \, \frac{\beta }{1-\beta } \,\, \text {d} \beta . \end{aligned}$$

Theorem A.10

[6] Let us assume that ${\zeta _{1}},{\zeta _{2}},{\zeta _{3}} ,\cdots ,{\zeta _{n}}$ be independent UVs with regular UDs $\Phi _1,\Phi _2,\cdots ,\Phi _n$ respectively and if $f:\mathfrak {R}^{n} \rightarrow \mathfrak {R}$ is a strictly increasing function w. r. to $x_{1},x_{2}, \cdots , x_{m}$ and strictly decreasing function w. r. to ${x_{m+1}},{x_{m+2}}, {x_{m+3}},\cdots ,{x_{n}}$, then the UV ${\zeta }=g\,({\zeta _1},{\zeta _2},{\zeta _3} ,\cdots ,{\zeta _n})$ has an entropy

$$\begin{aligned} H[\zeta ]= & {} \int _{0}^{1} g\,( \Phi _1^{-1}(\beta ),\Phi _2^{-1}(\beta ),\cdots , \Phi _m^{-1}(\beta ), \Phi _{m+1}^{-1}(1-\beta ),\cdots , \\&\Phi _{n}^{-1}(1-\beta ) ) \,\, \text {ln}\, \, \frac{\beta }{1-\beta } \,\, \text {d} \beta . \end{aligned}$$

Theorem A.11

[6] If ${\zeta _{1}}$ and ${\zeta _{2}}$ be two independent UVs with any $a_{1}, a_{2} \in \mathfrak {R}$, then we get

$$\begin{aligned} H[a_{1}\,{\zeta _{1}}+a_{2}\,{\zeta _{2}}]= |a_{1}|\,H[{\zeta _{1}}] +|a_{2}|\,H[{\zeta _{2}}]. \end{aligned}$$