Multi-objective uncertain project selection considering synergy

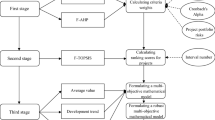
Abstract

This paper discusses a multi-objective mean-variance model and its solution algorithms for the project selection considering synergy under the uncertain environment. Two objective functions have been considered: maximizing the expected net present value (NPV) of the selected projects and minimizing the risk measured by variance of NPV. Here, the profits and investment outlays for candidate projects and synergistic profits and outlays of interdependent projects are considered as uncertain variables whose distributions are determined by experts’ evaluations. According to uncertainty theory, the deterministic equivalents are obtained. The effect of uncertainty on project selection is analyzed through comparison between the proposed uncertain model and the certain model with exact parameters. And the effect of synergy on the project selection is also analyzed. To get the Pareto-optimal solutions of the proposed multi-objective project selection model, we provide a new multi-objective modified binary Jaya (MOMB-Jaya) algorithm and a new multi-objective modified binary Rao (MOMB-Rao) algorithm, which respectively are modifications of the Jaya and Rao algorithms for solving the proposed multi-objective problems. Through numerical experiments on 15 example problems, including large-scale problems, the performances of the proposed multi-objective binary algorithms are tested. Comparison with the binary version of non-dominated teaching-learning-based optimization (NSTLBO) algorithm shows the better performance of the MOMB-Rao algorithm. Finally, a numerical example is given to demonstrate the validity of the proposed multi-objective uncertain model.

A Uncertainty Theory

To help understand uncertain portfolio selection, we provide the fundamentals of uncertainty theory used in out paper. For more knowledge, the readers can refer to [9].

The uncertain variable in uncertainty theory is characterized by an uncertainty distribution defined as below.

Definition 1

[9] For any real number t, the function $\Phi (t)$ defined by

$$\begin{aligned} \Phi (t)={{\mathcal {M}}}\left\{ \xi \leqslant t \right\} \end{aligned}$$

is called the uncertainty distribution of the uncertain variable $\xi$.

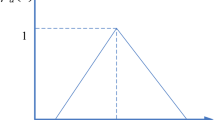
For a linear uncertain variable $\xi$, its uncertainty distribution is expressed as

$$\begin{aligned} \Phi (t) = \left\{ { \begin{array}{l} 0,\qquad \qquad \qquad \ \mathrm{if} \quad t < a \\ (t - a)/(b - a), \,\ \mathrm{if} \quad a \leqslant t \leqslant b \\ 1,\qquad \qquad \qquad \ \mathrm{if} \quad t > b \\ \end{array}}\right. ,\qquad t \in \mathfrak {R}. \end{aligned}$$

For convenience, the linear uncertainty distribution is denoted by $\xi \thicksim {{\mathcal {L}}}(a,b)$ where $a<b$.

For a normal uncertain variable $\xi$, its uncertainty distribution is expressed as

$$\begin{aligned} \Phi (t) = \left( {1 + \exp \left( {\frac{{\pi (\mu - t)}}{{\sqrt{3} \sigma }}} \right) } \right) ^{ - 1} , \qquad t \in \mathfrak {R}. \end{aligned}$$

For convenience, it is denoted by $\xi \thicksim {{\mathcal {N}}}(\mu ,\sigma )$ where $\mu$ and $\sigma$ are real numbers and $\sigma >0$.

[9].

Theorem 7

[9] Let uncertain variables $\xi _1, \xi _2, \ldots , \xi _n$ be independent and their uncertainty distributions $\Phi _1, \Phi _2, \ldots , \Phi _n$ be regular. If $f(\xi _1, \xi _2, \ldots , \xi _n)$ increases monotonically with respect to $\xi _1, \xi _2, \ldots , \xi _m$ and decreases monotonically with respect to $\xi _{m+1}, \xi _{m+2}, \ldots , \xi _n$, then the inverse uncertainty distribution of

$$\begin{aligned} \xi = f(\xi _1, \xi _2, \ldots , \xi _n) \end{aligned}$$

is expressed as

$$\begin{aligned} \Psi ^{-1}(\alpha ) = f(\Phi _1^{-1}(\alpha ), \Phi _2^{-1}(\alpha ), \ldots , \Phi _m^{-1}(\alpha ), \Phi _{m+1}^{-1}(1-\alpha ), \ldots , \Phi _n^{-1}(1-\alpha )), \qquad 0<\alpha <1. \end{aligned}$$

Definition 2

[9] The quantity $E[\xi ]$ defined by

$$\begin{aligned} E[\xi ] = \int \limits _0^{ + \infty } {{{\mathcal {M}}} \left\{ \xi \geqslant t\right\} dt} - \int \limits _{ - \infty }^0 {{{\mathcal {M}}}\left\{ \xi \leqslant t\right\} dt} \end{aligned}$$

is called the expected value of the uncertain variable $\xi$ if at least one of the two integrals is finite.

Theorem 8

Let $\xi$ be an uncertain variable and $\Phi$ be a regular uncertainty distribution of $\xi$. If there exists the expected value of $\xi$, then

$$\begin{aligned} E[\xi ] = \int \limits _0^1 {\Phi ^{-1}(\alpha )d\alpha }. \end{aligned}$$

Definition 3

[9] Let $\xi$ be an uncertain variable and $\mu$ be a finite expected value of $\xi$. Then the quantity $V[\xi ]$ defined by

$$\begin{aligned} V[\xi ] = E[(\xi - \mu )^2]. \end{aligned}$$

is called the variance of the uncertain variable $\xi$, and the square root of the variance is called the standard deviation of $\xi$.

Theorem 9

[9] Let $\xi$ be an uncertain variable, $\Phi$ be a regular uncertainty distribution of $\xi$ and $\mu$ be a finite expected value of $\xi$. Then

$$\begin{aligned} V[\xi ] = \int \limits _0^1 {\left( \Phi ^{-1}(\alpha ) - \mu \right) }^2d\alpha . \end{aligned}$$